Patch-based adaptive temporal filter and residual evaluation

In coherent imaging systems, speckle is a signal-dependent noise that visually strongly degrades images' appearance. A huge amount of SAR data has been acquired from different sensors with different wavelengths, resolutions, incidences and polarizations. We extend the nonlocal filtering strategy to the temporal domain and propose a patch-based adaptive temporal filter (PATF) to take advantage of well-registered multi-temporal SAR images. A patch-based generalised likelihood ratio test is processed to suppress the changed object effects on the multitemporal denoising results. Then, the similarities are transformed into corresponding weights with an exponential function. The denoised value is calculated with a temporal weighted average. Spatial adaptive denoising methods can improve the patch-based weighted temporal average image when the time series is limited. The spatial adaptive denoising step is optional when the time series is large enough. Without reference image, we propose using a patch-based auto-covariance residual evaluation method to examine the ratio image between the noisy and denoised images and look for possible remaining structural contents. It can process automatically and does not rely on a supervised selection of homogeneous regions. It also provides a global score for the whole image. Numerous results demonstrate the effectiveness of the proposed time series denoising method and the usefulness of the residual evaluation method.

Multitemporal SAR images change detection and visualization using RABASAR and simplified GLR

Understanding the state of changed areas requires that precise information be given about the changes. Thus, detecting different kinds of changes is important for land surface monitoring. SAR sensors are ideal to fulfil this task, because of their all-time and all-weather capabilities, with good accuracy of the acquisition geometry and without effects of atmospheric constituents for amplitude data. In this study, we propose a simplified generalized likelihood ratio ($S_{GLR}$) method assuming that corresponding temporal pixels have the same equivalent number of looks (ENL). Thanks to the denoised data provided by a ratio-based multitemporal SAR image denoising method (RABASAR), we successfully applied this similarity test approach to compute the change areas. A new change magnitude index method and an improved spectral clustering-based change classification method are also developed. In addition, we apply the simplified generalized likelihood ratio to detect the maximum change magnitude time, and the change starting and ending times. Then, we propose to use an adaptation of the REACTIV method to visualize the detection results vividly. The effectiveness of the proposed methods is demonstrated through the processing of simulated and SAR images, and the comparison with classical techniques. In particular, numerical experiments proved that the developed method has good performances in detecting farmland area changes, building area changes, harbour area changes and flooding area changes.

Gradient-Based Deep Quantization of Neural Networks through Sinusoidal Adaptive Regularization

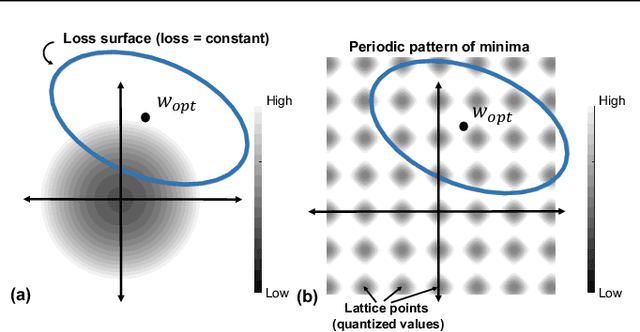
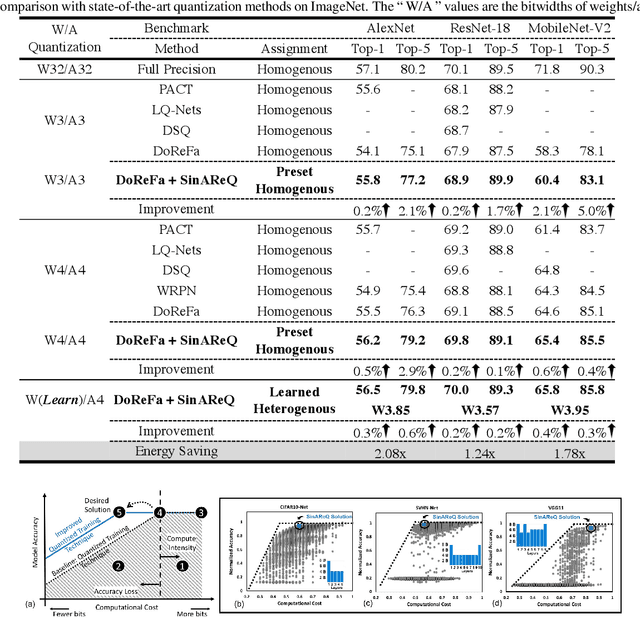
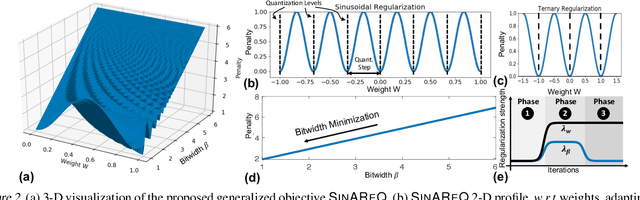
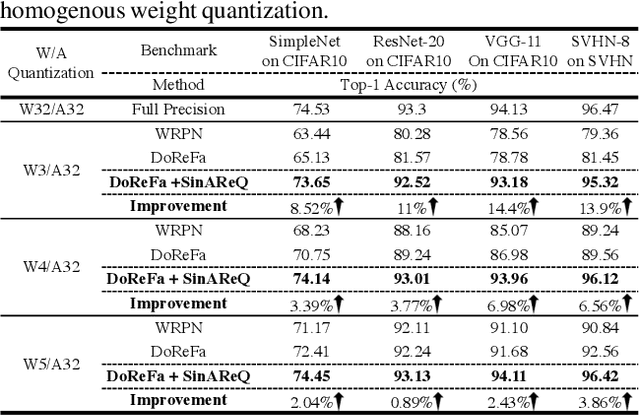
As deep neural networks make their ways into different domains, their compute efficiency is becoming a first-order constraint. Deep quantization, which reduces the bitwidth of the operations (below 8 bits), offers a unique opportunity as it can reduce both the storage and compute requirements of the network super-linearly. However, if not employed with diligence, this can lead to significant accuracy loss. Due to the strong inter-dependence between layers and exhibiting different characteristics across the same network, choosing an optimal bitwidth per layer granularity is not a straight forward. As such, deep quantization opens a large hyper-parameter space, the exploration of which is a major challenge. We propose a novel sinusoidal regularization, called SINAREQ, for deep quantized training. Leveraging the sinusoidal properties, we seek to learn multiple quantization parameterization in conjunction during gradient-based training process. Specifically, we learn (i) a per-layer quantization bitwidth along with (ii) a scale factor through learning the period of the sinusoidal function. At the same time, we exploit the periodicity, differentiability, and the local convexity profile in sinusoidal functions to automatically propel (iii) network weights towards values quantized at levels that are jointly determined. We show how SINAREQ balance compute efficiency and accuracy, and provide a heterogeneous bitwidth assignment for quantization of a large variety of deep networks (AlexNet, CIFAR-10, MobileNet, ResNet-18, ResNet-20, SVHN, and VGG-11) that virtually preserves the accuracy. Furthermore, we carry out experimentation using fixed homogenous bitwidths with 3- to 5-bit assignment and show the versatility of SINAREQ in enhancing quantized training algorithms (DoReFa and WRPN) with about 4.8% accuracy improvements on average, and then outperforming multiple state-of-the-art techniques.

Machine learning in acoustics: a review

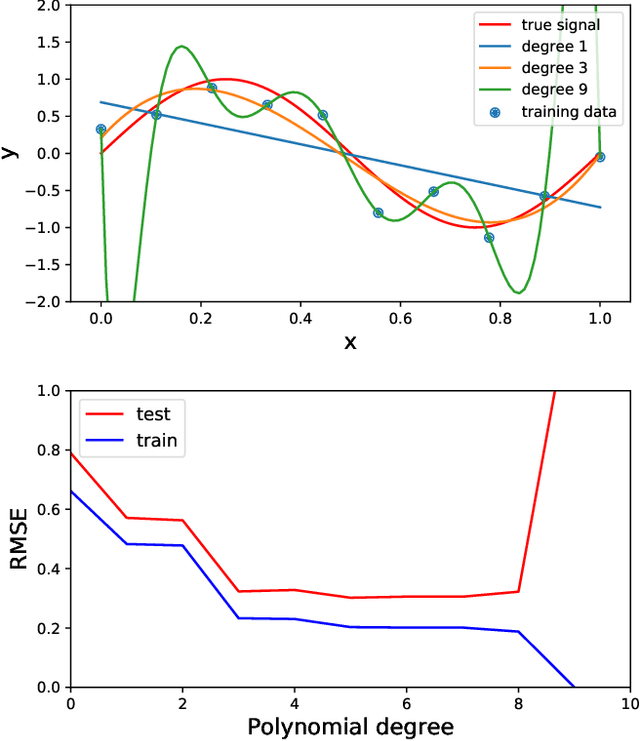
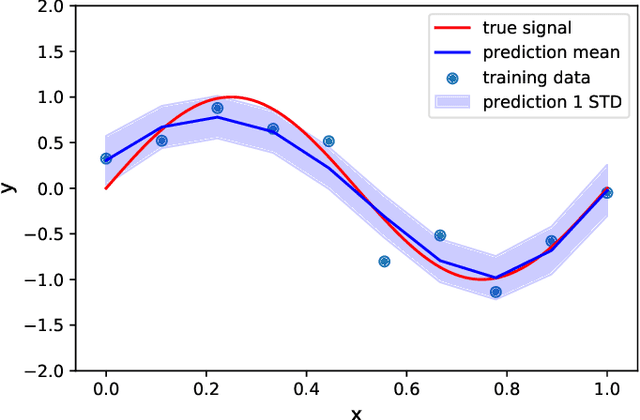
Acoustic data provide scientific and engineering insights in fields ranging from biology and communications to ocean and Earth science. We survey the recent advances and transformative potential of machine learning (ML), including deep learning, in the field of acoustics. ML is a broad family of statistical techniques for automatically detecting and utilizing patterns in data. Relative to conventional acoustics and signal processing, ML is data-driven. Given sufficient training data, ML can discover complex relationships between features. With large volumes of training data, ML can discover models describing complex acoustic phenomena such as human speech and reverberation. ML in acoustics is rapidly developing with compelling results and significant future promise. We first introduce ML, then highlight ML developments in five acoustics research areas: source localization in speech processing, source localization in ocean acoustics, bioacoustics, seismic exploration, and environmental sounds in everyday scenes.

Image denoising with generalized Gaussian mixture model patch priors

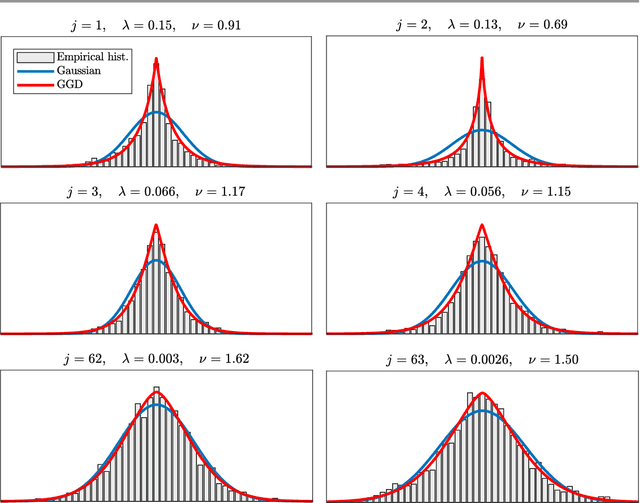
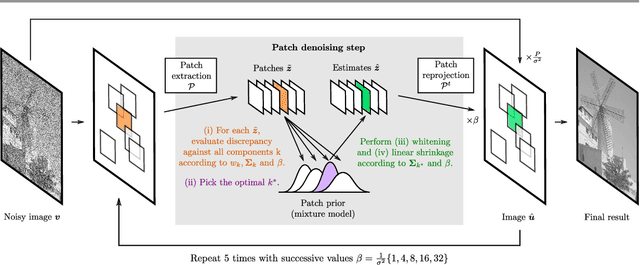
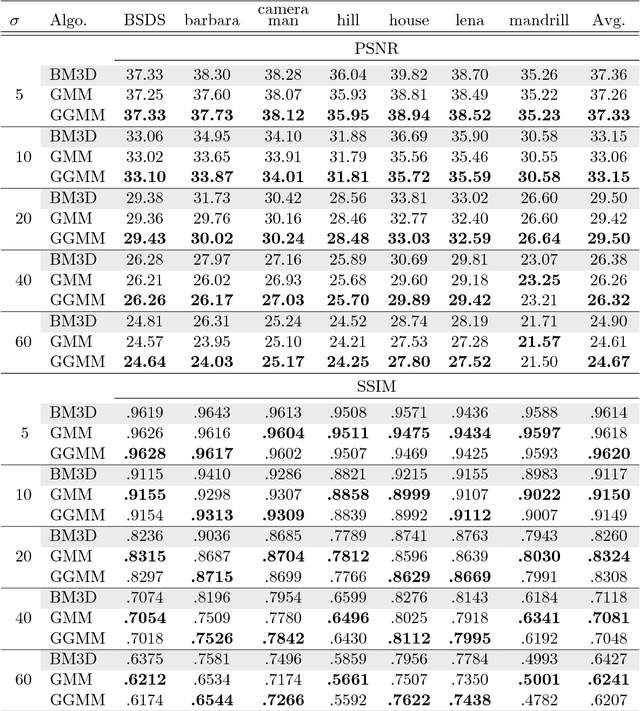
Patch priors have become an important component of image restoration. A powerful approach in this category of restoration algorithms is the popular Expected Patch Log-Likelihood (EPLL) algorithm. EPLL uses a Gaussian mixture model (GMM) prior learned on clean image patches as a way to regularize degraded patches. In this paper, we show that a generalized Gaussian mixture model (GGMM) captures the underlying distribution of patches better than a GMM. Even though GGMM is a powerful prior to combine with EPLL, the non-Gaussianity of its components presents major challenges to be applied to a computationally intensive process of image restoration. Specifically, each patch has to undergo a patch classification step and a shrinkage step. These two steps can be efficiently solved with a GMM prior but are computationally impractical when using a GGMM prior. In this paper, we provide approximations and computational recipes for fast evaluation of these two steps, so that EPLL can embed a GGMM prior on an image with more than tens of thousands of patches. Our main contribution is to analyze the accuracy of our approximations based on thorough theoretical analysis. Our evaluations indicate that the GGMM prior is consistently a better fit formodeling image patch distribution and performs better on average in image denoising task.

Parameter Estimation in Finite Mixture Models by Regularized Optimal Transport: A Unified Framework for Hard and Soft Clustering

In this short paper, we formulate parameter estimation for finite mixture models in the context of discrete optimal transportation with convex regularization. The proposed framework unifies hard and soft clustering methods for general mixture models. It also generalizes the celebrated $k$\nobreakdash-means and expectation-maximization algorithms in relation to associated Bregman divergences when applied to exponential family mixture models.

Accelerating GMM-based patch priors for image restoration: Three ingredients for a 100$\times$ speed-up

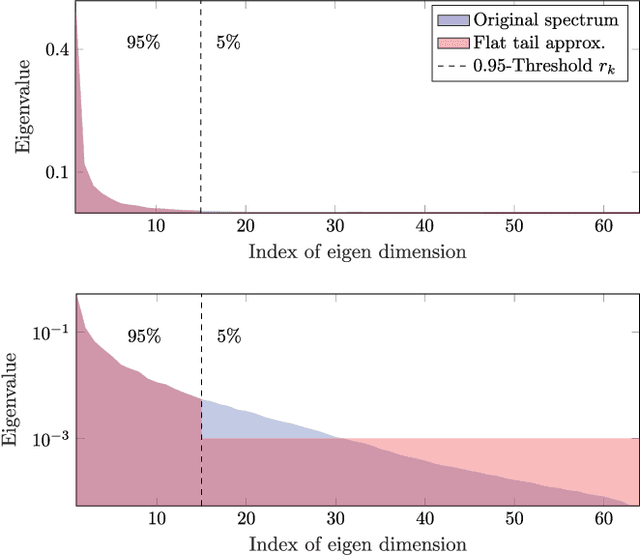
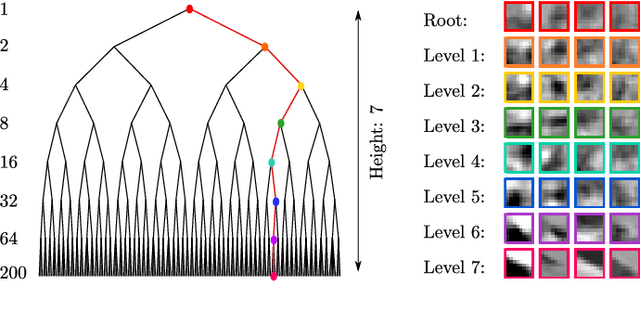
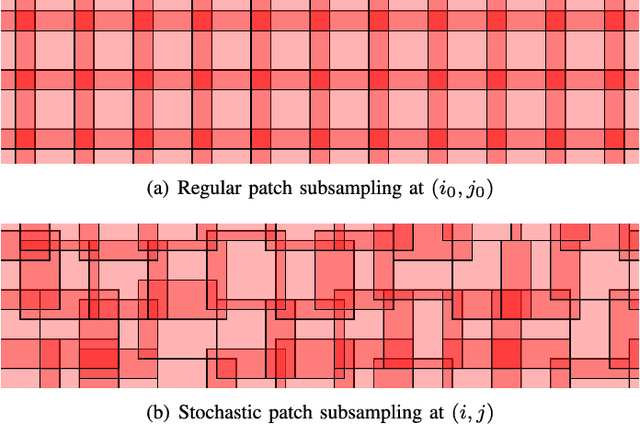
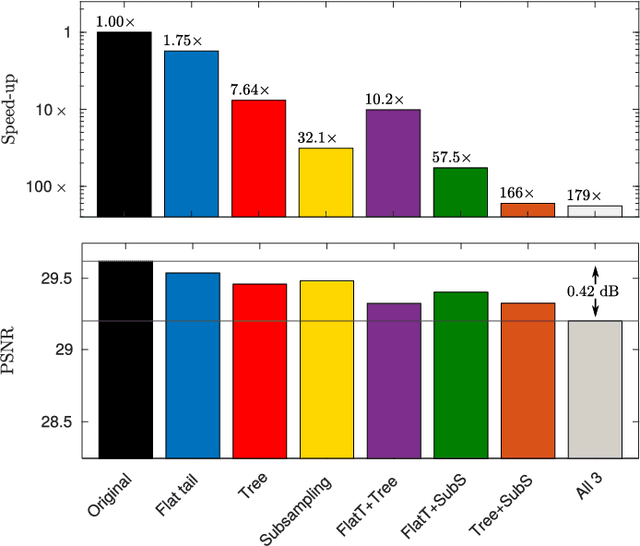
Image restoration methods aim to recover the underlying clean image from corrupted observations. The Expected Patch Log-likelihood (EPLL) algorithm is a powerful image restoration method that uses a Gaussian mixture model (GMM) prior on the patches of natural images. Although it is very effective for restoring images, its high runtime complexity makes EPLL ill-suited for most practical applications. In this paper, we propose three approximations to the original EPLL algorithm. The resulting algorithm, which we call the fast-EPLL (FEPLL), attains a dramatic speed-up of two orders of magnitude over EPLL while incurring a negligible drop in the restored image quality (less than 0.5 dB). We demonstrate the efficacy and versatility of our algorithm on a number of inverse problems such as denoising, deblurring, super-resolution, inpainting and devignetting. To the best of our knowledge, FEPLL is the first algorithm that can competitively restore a 512x512 pixel image in under 0.5s for all the degradations mentioned above without specialized code optimizations such as CPU parallelization or GPU implementation.

Characterizing the maximum parameter of the total-variation denoising through the pseudo-inverse of the divergence

We focus on the maximum regularization parameter for anisotropic total-variation denoising. It corresponds to the minimum value of the regularization parameter above which the solution remains constant. While this value is well know for the Lasso, such a critical value has not been investigated in details for the total-variation. Though, it is of importance when tuning the regularization parameter as it allows fixing an upper-bound on the grid for which the optimal parameter is sought. We establish a closed form expression for the one-dimensional case, as well as an upper-bound for the two-dimensional case, that appears reasonably tight in practice. This problem is directly linked to the computation of the pseudo-inverse of the divergence, which can be quickly obtained by performing convolutions in the Fourier domain.

Poisson noise reduction with non-local PCA

Photon-limited imaging arises when the number of photons collected by a sensor array is small relative to the number of detector elements. Photon limitations are an important concern for many applications such as spectral imaging, night vision, nuclear medicine, and astronomy. Typically a Poisson distribution is used to model these observations, and the inherent heteroscedasticity of the data combined with standard noise removal methods yields significant artifacts. This paper introduces a novel denoising algorithm for photon-limited images which combines elements of dictionary learning and sparse patch-based representations of images. The method employs both an adaptation of Principal Component Analysis (PCA) for Poisson noise and recently developed sparsity-regularized convex optimization algorithms for photon-limited images. A comprehensive empirical evaluation of the proposed method helps characterize the performance of this approach relative to other state-of-the-art denoising methods. The results reveal that, despite its conceptual simplicity, Poisson PCA-based denoising appears to be highly competitive in very low light regimes.

Risk estimation for matrix recovery with spectral regularization

In this paper, we develop an approach to recursively estimate the quadratic risk for matrix recovery problems regularized with spectral functions. Toward this end, in the spirit of the SURE theory, a key step is to compute the (weak) derivative and divergence of a solution with respect to the observations. As such a solution is not available in closed form, but rather through a proximal splitting algorithm, we propose to recursively compute the divergence from the sequence of iterates. A second challenge that we unlocked is the computation of the (weak) derivative of the proximity operator of a spectral function. To show the potential applicability of our approach, we exemplify it on a matrix completion problem to objectively and automatically select the regularization parameter.