CATCH-FORM-ACTer: Compliance-Aware Tactile Control and Hybrid Deformation Regulation-Based Action Transformer for Viscoelastic Object Manipulation

Automating contact-rich manipulation of viscoelastic objects with rigid robots faces challenges including dynamic parameter mismatches, unstable contact oscillations, and spatiotemporal force-deformation coupling. In our prior work, a Compliance-Aware Tactile Control and Hybrid Deformation Regulation (CATCH-FORM-3D) strategy fulfills robust and effective manipulations of 3D viscoelastic objects, which combines a contact force-driven admittance outer loop and a PDE-stabilized inner loop, achieving sub-millimeter surface deformation accuracy. However, this strategy requires fine-tuning of object-specific parameters and task-specific calibrations, to bridge this gap, a CATCH-FORM-ACTer is proposed, by enhancing CATCH-FORM-3D with a framework of Action Chunking with Transformer (ACT). An intuitive teleoperation system performs Learning from Demonstration (LfD) to build up a long-horizon sensing, decision-making and execution sequences. Unlike conventional ACT methods focused solely on trajectory planning, our approach dynamically adjusts stiffness, damping, and diffusion parameters in real time during multi-phase manipulations, effectively imitating human-like force-deformation modulation. Experiments on single arm/bimanual robots in three tasks show better force fields patterns and thus 10%-20% higher success rates versus conventional methods, enabling precise, safe interactions for industrial, medical or household scenarios.

CATCH-FORM-3D: Compliance-Aware Tactile Control and Hybrid Deformation Regulation for 3D Viscoelastic Object Manipulation

This paper investigates a framework (CATCH-FORM-3D) for the precise contact force control and surface deformation regulation in viscoelastic material manipulation. A partial differential equation (PDE) is proposed to model the spatiotemporal stress-strain dynamics, integrating 3D Kelvin-Voigt (stiffness-damping) and Maxwell (diffusion) effects to capture the material's viscoelastic behavior. Key mechanical parameters (stiffness, damping, diffusion coefficients) are estimated in real time via a PDE-driven observer. This observer fuses visual-tactile sensor data and experimentally validated forces to generate rich regressor signals. Then, an inner-outer loop control structure is built up. In the outer loop, the reference deformation is updated by a novel admittance control law, a proportional-derivative (PD) feedback law with contact force measurements, ensuring that the system responds adaptively to external interactions. In the inner loop, a reaction-diffusion PDE for the deformation tracking error is formulated and then exponentially stabilized by conforming the contact surface to analytical geometric configurations (i.e., defining Dirichlet boundary conditions). This dual-loop architecture enables the effective deformation regulation in dynamic contact environments. Experiments using a PaXini robotic hand demonstrate sub-millimeter deformation accuracy and stable force tracking. The framework advances compliant robotic interactions in applications like industrial assembly, polymer shaping, surgical treatment, and household service.

Generalized Temporal Tensor Decomposition with Rank-revealing Latent-ODE

Tensor decomposition is a fundamental tool for analyzing multi-dimensional data by learning low-rank factors to represent high-order interactions. While recent works on temporal tensor decomposition have made significant progress by incorporating continuous timestamps in latent factors, they still struggle with general tensor data with continuous indexes not only in the temporal mode but also in other modes, such as spatial coordinates in climate data. Additionally, the problem of determining the tensor rank remains largely unexplored in temporal tensor models. To address these limitations, we propose \underline{G}eneralized temporal tensor decomposition with \underline{R}ank-r\underline{E}vealing laten\underline{T}-ODE (GRET). Our approach encodes continuous spatial indexes as learnable Fourier features and employs neural ODEs in latent space to learn the temporal trajectories of factors. To automatically reveal the rank of temporal tensors, we introduce a rank-revealing Gaussian-Gamma prior over the factor trajectories. We develop an efficient variational inference scheme with an analytical evidence lower bound, enabling sampling-free optimization. Through extensive experiments on both synthetic and real-world datasets, we demonstrate that GRET not only reveals the underlying ranks of temporal tensors but also significantly outperforms existing methods in prediction performance and robustness against noise.

Machine learning in acoustics: a review

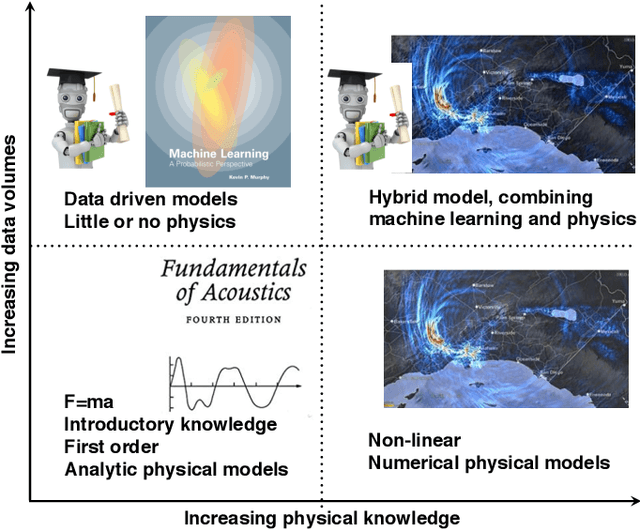
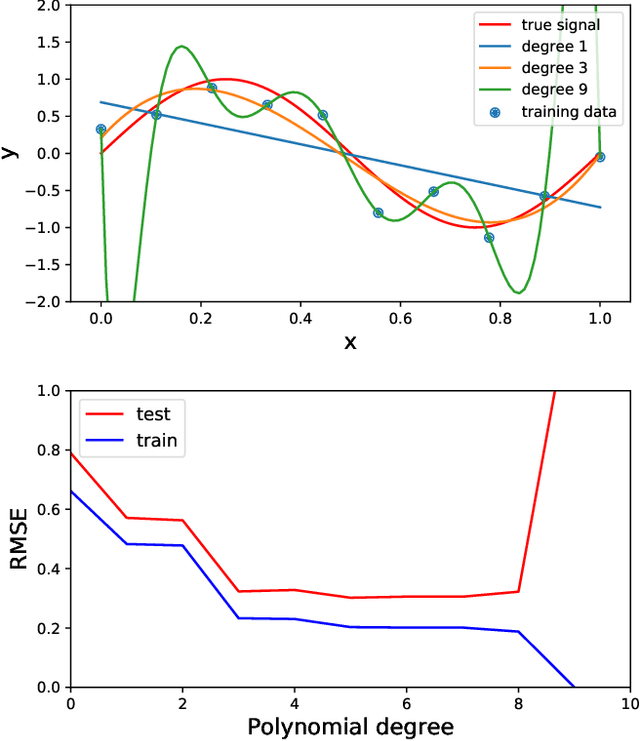
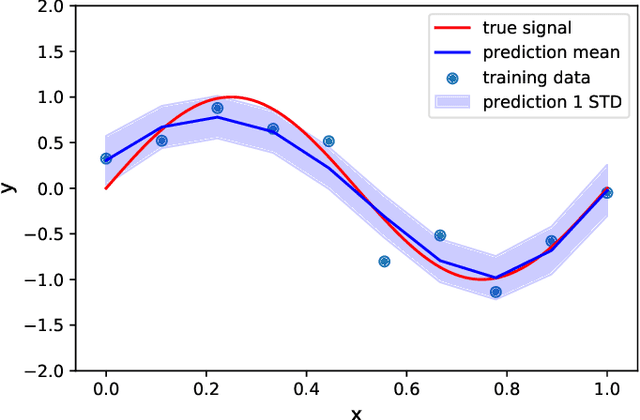
Acoustic data provide scientific and engineering insights in fields ranging from biology and communications to ocean and Earth science. We survey the recent advances and transformative potential of machine learning (ML), including deep learning, in the field of acoustics. ML is a broad family of statistical techniques for automatically detecting and utilizing patterns in data. Relative to conventional acoustics and signal processing, ML is data-driven. Given sufficient training data, ML can discover complex relationships between features. With large volumes of training data, ML can discover models describing complex acoustic phenomena such as human speech and reverberation. ML in acoustics is rapidly developing with compelling results and significant future promise. We first introduce ML, then highlight ML developments in five acoustics research areas: source localization in speech processing, source localization in ocean acoustics, bioacoustics, seismic exploration, and environmental sounds in everyday scenes.