Less Is More: Generating Time Series with LLaMA-Style Autoregression in Simple Factorized Latent Spaces

Generative models for multivariate time series are essential for data augmentation, simulation, and privacy preservation, yet current state-of-the-art diffusion-based approaches are slow and limited to fixed-length windows. We propose FAR-TS, a simple yet effective framework that combines disentangled factorization with an autoregressive Transformer over a discrete, quantized latent space to generate time series. Each time series is decomposed into a data-adaptive basis that captures static cross-channel correlations and temporal coefficients that are vector-quantized into discrete tokens. A LLaMA-style autoregressive Transformer then models these token sequences, enabling fast and controllable generation of sequences with arbitrary length. Owing to its streamlined design, FAR-TS achieves orders-of-magnitude faster generation than Diffusion-TS while preserving cross-channel correlations and an interpretable latent space, enabling high-quality and flexible time series synthesis.

Generalized Temporal Tensor Decomposition with Rank-revealing Latent-ODE

Tensor decomposition is a fundamental tool for analyzing multi-dimensional data by learning low-rank factors to represent high-order interactions. While recent works on temporal tensor decomposition have made significant progress by incorporating continuous timestamps in latent factors, they still struggle with general tensor data with continuous indexes not only in the temporal mode but also in other modes, such as spatial coordinates in climate data. Additionally, the problem of determining the tensor rank remains largely unexplored in temporal tensor models. To address these limitations, we propose \underline{G}eneralized temporal tensor decomposition with \underline{R}ank-r\underline{E}vealing laten\underline{T}-ODE (GRET). Our approach encodes continuous spatial indexes as learnable Fourier features and employs neural ODEs in latent space to learn the temporal trajectories of factors. To automatically reveal the rank of temporal tensors, we introduce a rank-revealing Gaussian-Gamma prior over the factor trajectories. We develop an efficient variational inference scheme with an analytical evidence lower bound, enabling sampling-free optimization. Through extensive experiments on both synthetic and real-world datasets, we demonstrate that GRET not only reveals the underlying ranks of temporal tensors but also significantly outperforms existing methods in prediction performance and robustness against noise.

Striking The Right Balance: Three-Dimensional Ocean Sound Speed Field Reconstruction Using Tensor Neural Networks

Accurately reconstructing a three-dimensional ocean sound speed field (3D SSF) is essential for various ocean acoustic applications, but the sparsity and uncertainty of sound speed samples across a vast ocean region make it a challenging task. To tackle this challenge, a large body of reconstruction methods has been developed, including spline interpolation, matrix/tensor-based completion, and deep neural networks-based reconstruction. However, a principled analysis of their effectiveness in 3D SSF reconstruction is still lacking. This paper performs a thorough analysis of the reconstruction error and highlights the need for a balanced representation model that integrates both expressiveness and conciseness. To meet this requirement, a 3D SSF-tailored tensor deep neural network is proposed, which utilizes tensor computations and deep neural network architectures to achieve remarkable 3D SSF reconstruction. The proposed model not only includes the previous tensor-based SSF representation model as a special case, but also has a natural ability to reject noise. The numerical results using the South China Sea 3D SSF data demonstrate that the proposed method outperforms state-of-the-art methods. The code is available at https://github.com/OceanSTARLab/Tensor-Neural-Network.

Tensor-based Basis Function Learning for Three-dimensional Sound Speed Fields

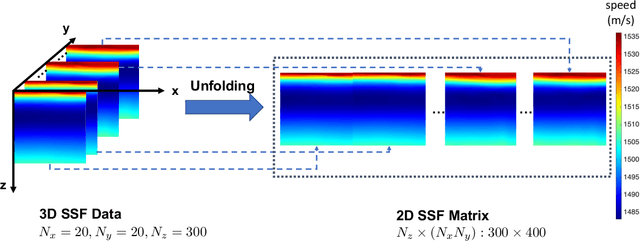
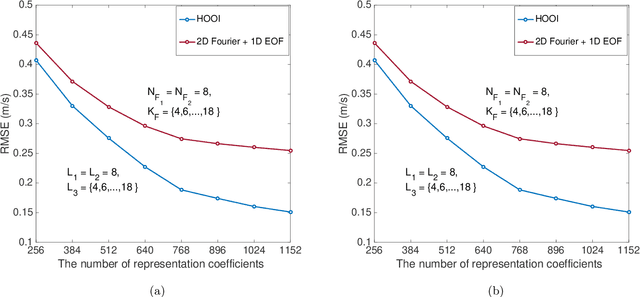
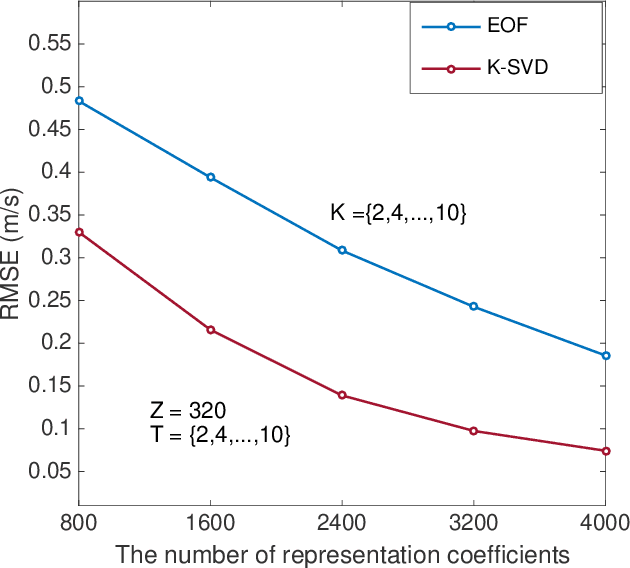
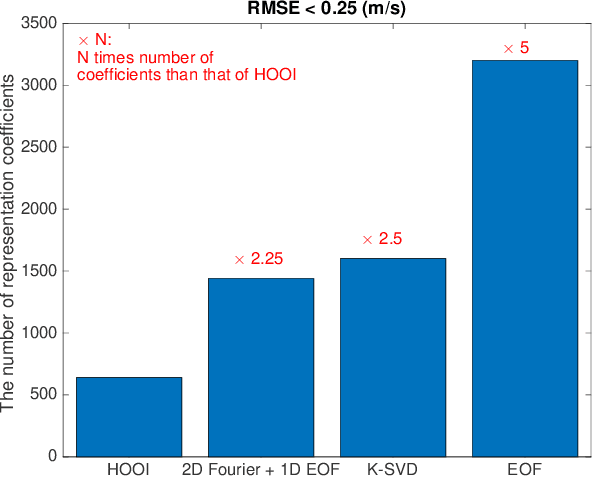
Basis function learning is the stepping stone towards effective three-dimensional (3D) sound speed field (SSF) inversion for various acoustic signal processing tasks, including ocean acoustic tomography, underwater target localization/tracking, and underwater communications. Classical basis functions include the empirical orthogonal functions (EOFs), Fourier basis functions, and their combinations. The unsupervised machine learning method, e.g., the K-SVD algorithm, has recently tapped into the basis function design, showing better representation performance than the EOFs. However, existing methods do not consider basis function learning approaches that treat 3D SSF data as a third-order tensor, and thus cannot fully utilize the 3D interactions/correlations therein. To circumvent such a drawback, basis function learning is linked to tensor decomposition in this paper, which is the primary drive for recent multi-dimensional data mining. In particular, a tensor-based basis function learning framework is proposed, which can include the classical basis functions (using EOFs and/or Fourier basis functions) as its special cases. This provides a unified tensor perspective for understanding and representing 3D SSFs. Numerical results using the South China Sea 3D SSF data have demonstrated the excellent performance of the tensor-based basis functions.