Parameter Estimation in Finite Mixture Models by Regularized Optimal Transport: A Unified Framework for Hard and Soft Clustering
Paper and Code
Nov 12, 2017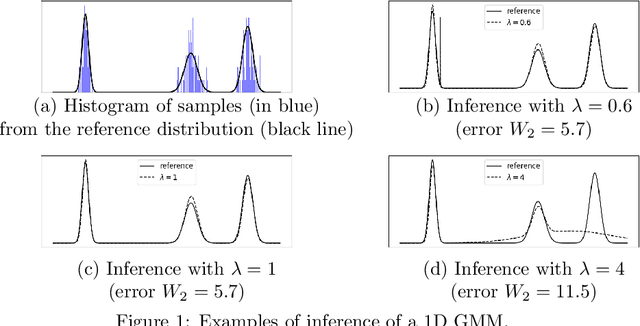
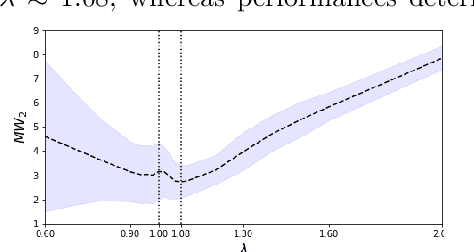
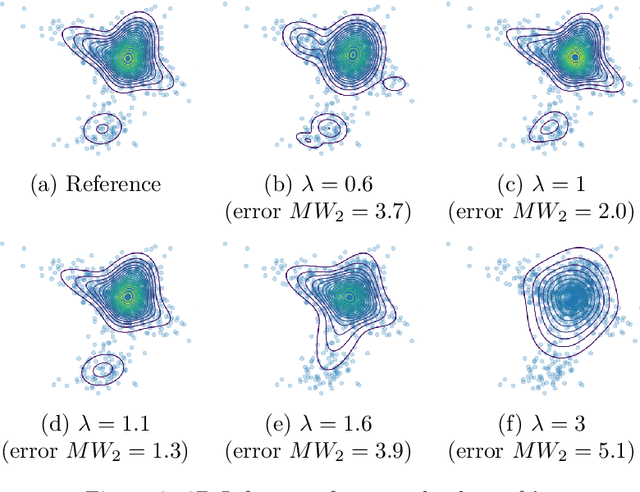
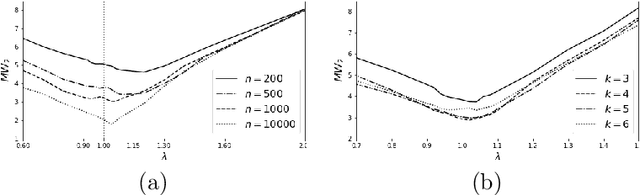
In this short paper, we formulate parameter estimation for finite mixture models in the context of discrete optimal transportation with convex regularization. The proposed framework unifies hard and soft clustering methods for general mixture models. It also generalizes the celebrated $k$\nobreakdash-means and expectation-maximization algorithms in relation to associated Bregman divergences when applied to exponential family mixture models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge