Implicit Regularization in Deep Learning: A View from Function Space

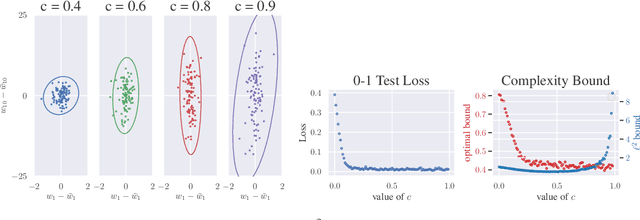
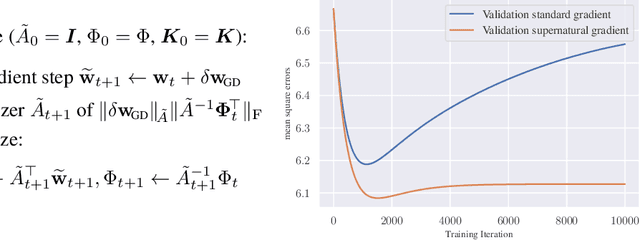
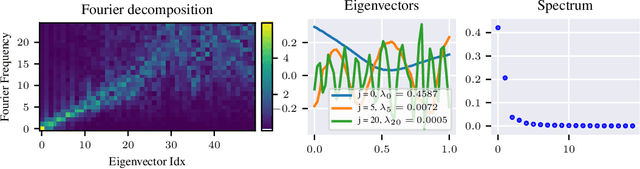
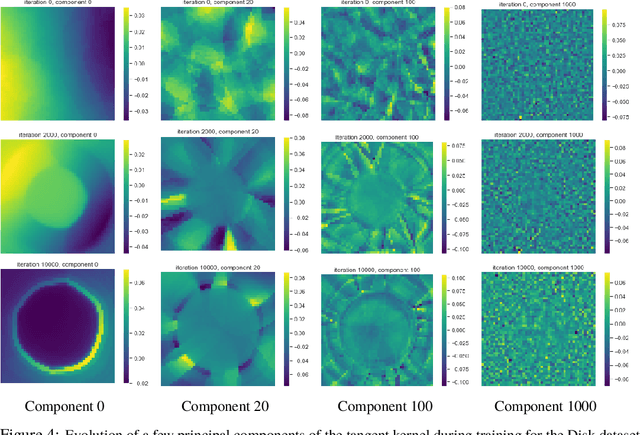
We approach the problem of implicit regularization in deep learning from a geometrical viewpoint. We highlight a possible regularization effect induced by a dynamical alignment of the neural tangent features introduced by Jacot et al, along a small number of task-relevant directions. By extrapolating a new analysis of Rademacher complexity bounds in linear models, we propose and study a new heuristic complexity measure for neural networks which captures this phenomenon, in terms of sequences of tangent kernel classes along in the learning trajectories.

Revisiting Loss Modelling for Unstructured Pruning

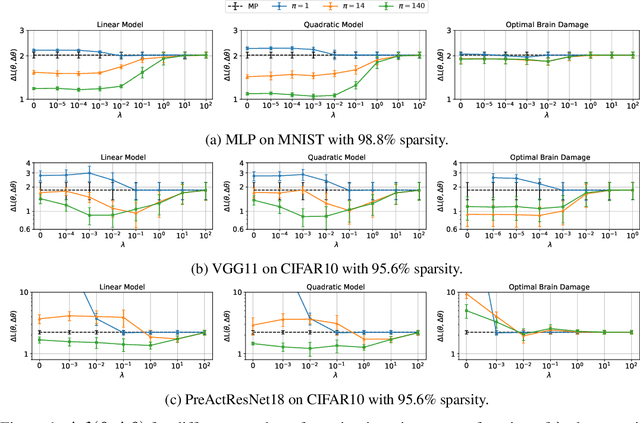
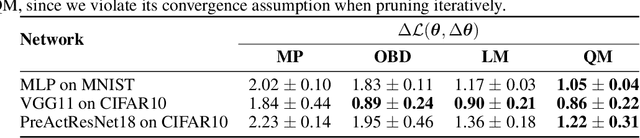
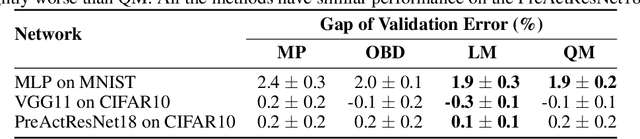
By removing parameters from deep neural networks, unstructured pruning methods aim at cutting down memory footprint and computational cost, while maintaining prediction accuracy. In order to tackle this otherwise intractable problem, many of these methods model the loss landscape using first or second order Taylor expansions to identify which parameters can be discarded. We revisit loss modelling for unstructured pruning: we show the importance of ensuring locality of the pruning steps. We systematically compare first and second order Taylor expansions and empirically show that both can reach similar levels of performance. Finally, we show that better preserving the original network function does not necessarily transfer to better performing networks after fine-tuning, suggesting that only considering the impact of pruning on the loss might not be a sufficient objective to design good pruning criteria.

Fast Approximate Natural Gradient Descent in a Kronecker-factored Eigenbasis

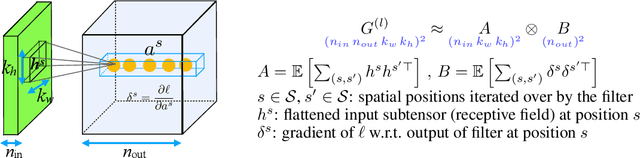
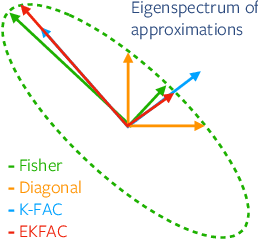
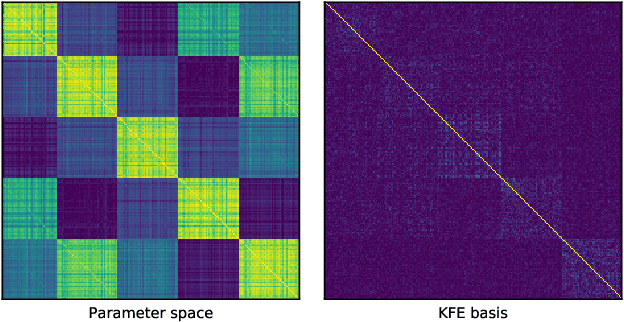
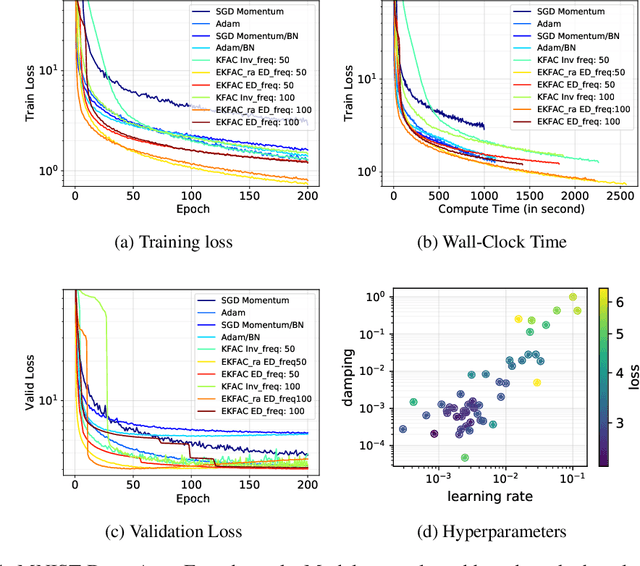
Optimization algorithms that leverage gradient covariance information, such as variants of natural gradient descent (Amari, 1998), offer the prospect of yielding more effective descent directions. For models with many parameters, the covariance matrix they are based on becomes gigantic, making them inapplicable in their original form. This has motivated research into both simple diagonal approximations and more sophisticated factored approximations such as KFAC (Heskes, 2000; Martens & Grosse, 2015; Grosse & Martens, 2016). In the present work we draw inspiration from both to propose a novel approximation that is provably better than KFAC and amendable to cheap partial updates. It consists in tracking a diagonal variance, not in parameter coordinates, but in a Kronecker-factored eigenbasis, in which the diagonal approximation is likely to be more effective. Experiments show improvements over KFAC in optimization speed for several deep network architectures.

Recurrent Batch Normalization

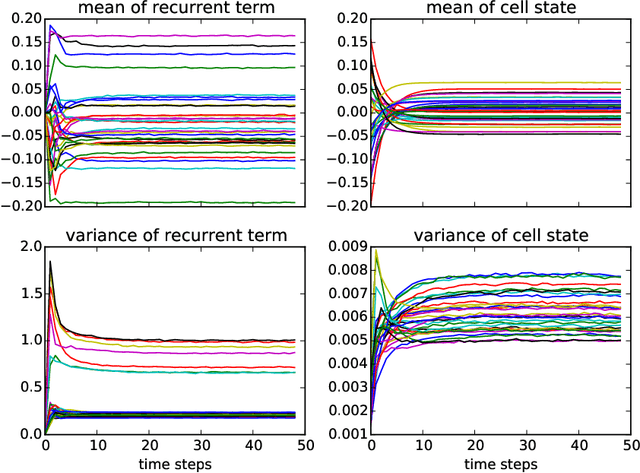
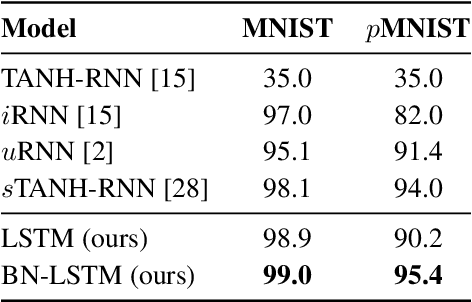
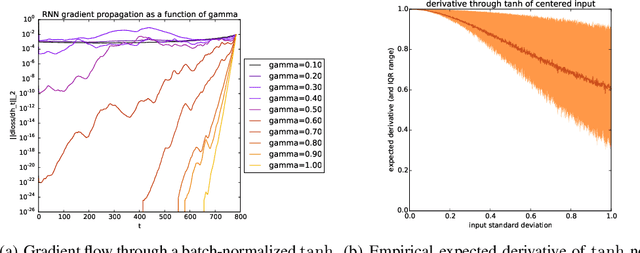
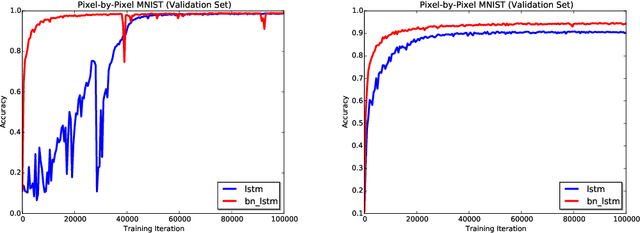
We propose a reparameterization of LSTM that brings the benefits of batch normalization to recurrent neural networks. Whereas previous works only apply batch normalization to the input-to-hidden transformation of RNNs, we demonstrate that it is both possible and beneficial to batch-normalize the hidden-to-hidden transition, thereby reducing internal covariate shift between time steps. We evaluate our proposal on various sequential problems such as sequence classification, language modeling and question answering. Our empirical results show that our batch-normalized LSTM consistently leads to faster convergence and improved generalization.

Theano: A Python framework for fast computation of mathematical expressions

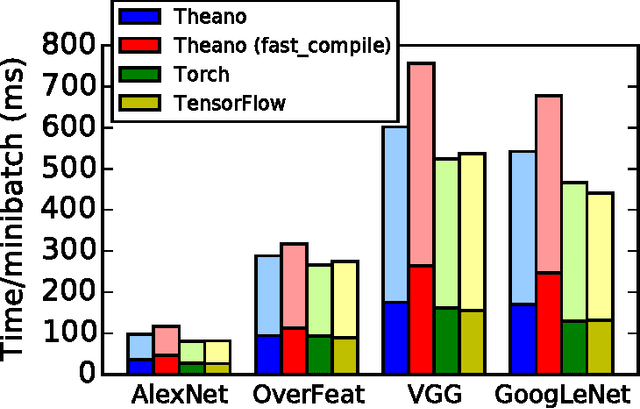
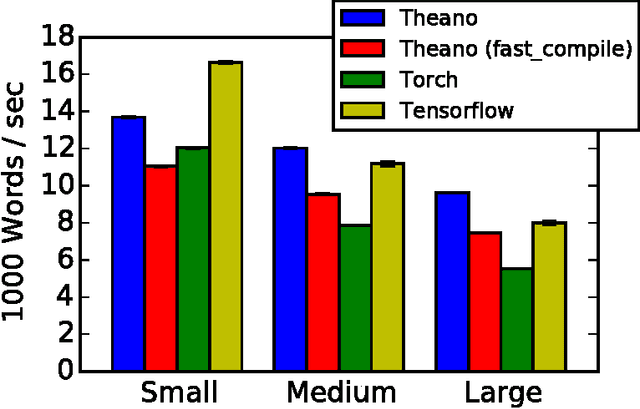
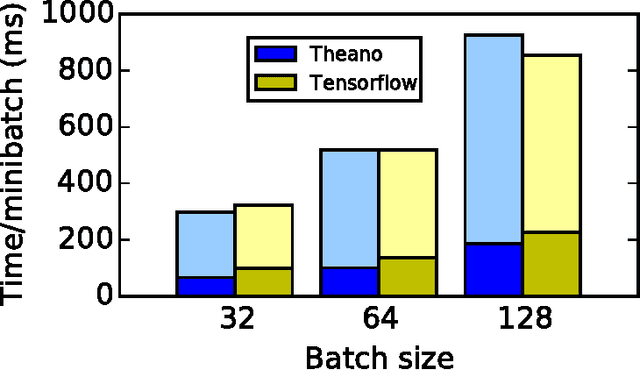
Theano is a Python library that allows to define, optimize, and evaluate mathematical expressions involving multi-dimensional arrays efficiently. Since its introduction, it has been one of the most used CPU and GPU mathematical compilers - especially in the machine learning community - and has shown steady performance improvements. Theano is being actively and continuously developed since 2008, multiple frameworks have been built on top of it and it has been used to produce many state-of-the-art machine learning models. The present article is structured as follows. Section I provides an overview of the Theano software and its community. Section II presents the principal features of Theano and how to use them, and compares them with other similar projects. Section III focuses on recently-introduced functionalities and improvements. Section IV compares the performance of Theano against Torch7 and TensorFlow on several machine learning models. Section V discusses current limitations of Theano and potential ways of improving it.

Batch Normalized Recurrent Neural Networks

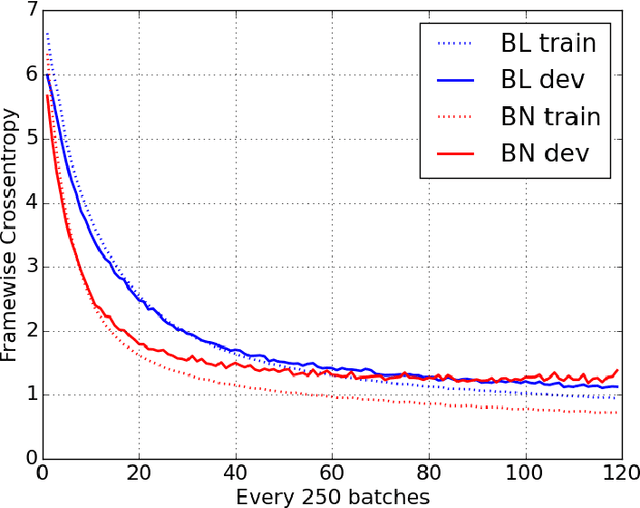
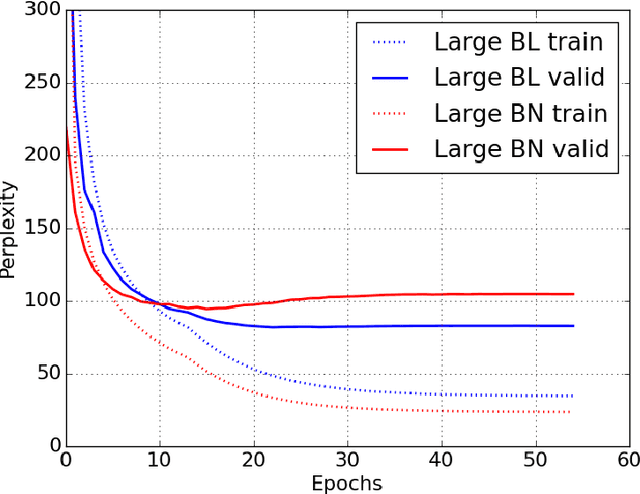
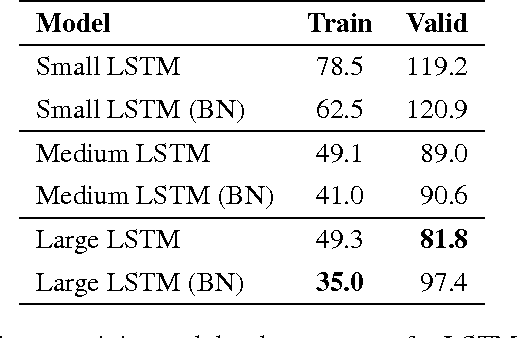
Recurrent Neural Networks (RNNs) are powerful models for sequential data that have the potential to learn long-term dependencies. However, they are computationally expensive to train and difficult to parallelize. Recent work has shown that normalizing intermediate representations of neural networks can significantly improve convergence rates in feedforward neural networks . In particular, batch normalization, which uses mini-batch statistics to standardize features, was shown to significantly reduce training time. In this paper, we show that applying batch normalization to the hidden-to-hidden transitions of our RNNs doesn't help the training procedure. We also show that when applied to the input-to-hidden transitions, batch normalization can lead to a faster convergence of the training criterion but doesn't seem to improve the generalization performance on both our language modelling and speech recognition tasks. All in all, applying batch normalization to RNNs turns out to be more challenging than applying it to feedforward networks, but certain variants of it can still be beneficial.