Bowen Fang
ToolWeaver: Weaving Collaborative Semantics for Scalable Tool Use in Large Language Models
Jan 29, 2026Abstract:Prevalent retrieval-based tool-use pipelines struggle with a dual semantic challenge: their retrievers often employ encoders that fail to capture complex semantics, while the Large Language Model (LLM) itself lacks intrinsic tool knowledge from its natural language pretraining. Generative methods offer a powerful alternative by unifying selection and execution, tasking the LLM to directly learn and generate tool identifiers. However, the common practice of mapping each tool to a unique new token introduces substantial limitations: it creates a scalability and generalization crisis, as the vocabulary size explodes and each tool is assigned a semantically isolated token. This approach also creates a semantic bottleneck that hinders the learning of collaborative tool relationships, as the model must infer them from sparse co-occurrences of monolithic tool IDs within a vast library. To address these limitations, we propose ToolWeaver, a novel generative tool learning framework that encodes tools into hierarchical sequences. This approach makes vocabulary expansion logarithmic to the number of tools. Crucially, it enables the model to learn collaborative patterns from the dense co-occurrence of shared codes, rather than the sparse co-occurrence of monolithic tool IDs. We generate these structured codes through a novel tokenization process designed to weave together a tool's intrinsic semantics with its extrinsic co-usage patterns. These structured codes are then integrated into the LLM through a generative alignment stage, where the model is fine-tuned to produce the hierarchical code sequences. Evaluation results with nearly 47,000 tools show that ToolWeaver significantly outperforms state-of-the-art methods, establishing a more scalable, generalizable, and semantically-aware foundation for advanced tool-augmented agents.
GenPilot: A Multi-Agent System for Test-Time Prompt Optimization in Image Generation
Oct 08, 2025Abstract:Text-to-image synthesis has made remarkable progress, yet accurately interpreting complex and lengthy prompts remains challenging, often resulting in semantic inconsistencies and missing details. Existing solutions, such as fine-tuning, are model-specific and require training, while prior automatic prompt optimization (APO) approaches typically lack systematic error analysis and refinement strategies, resulting in limited reliability and effectiveness. Meanwhile, test-time scaling methods operate on fixed prompts and on noise or sample numbers, limiting their interpretability and adaptability. To solve these, we introduce a flexible and efficient test-time prompt optimization strategy that operates directly on the input text. We propose a plug-and-play multi-agent system called GenPilot, integrating error analysis, clustering-based adaptive exploration, fine-grained verification, and a memory module for iterative optimization. Our approach is model-agnostic, interpretable, and well-suited for handling long and complex prompts. Simultaneously, we summarize the common patterns of errors and the refinement strategy, offering more experience and encouraging further exploration. Experiments on DPG-bench and Geneval with improvements of up to 16.9% and 5.7% demonstrate the strong capability of our methods in enhancing the text and image consistency and structural coherence of generated images, revealing the effectiveness of our test-time prompt optimization strategy. The code is available at https://github.com/27yw/GenPilot.
EgoDemoGen: Novel Egocentric Demonstration Generation Enables Viewpoint-Robust Manipulation
Sep 26, 2025


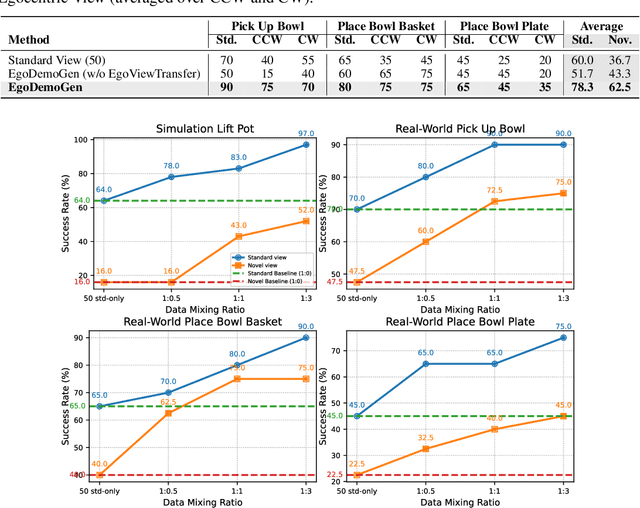
Abstract:Imitation learning based policies perform well in robotic manipulation, but they often degrade under *egocentric viewpoint shifts* when trained from a single egocentric viewpoint. To address this issue, we present **EgoDemoGen**, a framework that generates *paired* novel egocentric demonstrations by retargeting actions in the novel egocentric frame and synthesizing the corresponding egocentric observation videos with proposed generative video repair model **EgoViewTransfer**, which is conditioned by a novel-viewpoint reprojected scene video and a robot-only video rendered from the retargeted joint actions. EgoViewTransfer is finetuned from a pretrained video generation model using self-supervised double reprojection strategy. We evaluate EgoDemoGen on both simulation (RoboTwin2.0) and real-world robot. After training with a mixture of EgoDemoGen-generated novel egocentric demonstrations and original standard egocentric demonstrations, policy success rate improves **absolutely** by **+17.0%** for standard egocentric viewpoint and by **+17.7%** for novel egocentric viewpoints in simulation. On real-world robot, the **absolute** improvements are **+18.3%** and **+25.8%**. Moreover, performance continues to improve as the proportion of EgoDemoGen-generated demonstrations increases, with diminishing returns. These results demonstrate that EgoDemoGen provides a practical route to egocentric viewpoint-robust robotic manipulation.
DTPA: Dynamic Token-level Prefix Augmentation for Controllable Text Generation
Aug 06, 2025



Abstract:Controllable Text Generation (CTG) is a vital subfield in Natural Language Processing (NLP), aiming to generate text that aligns with desired attributes. However, previous studies commonly focus on the quality of controllable text generation for short sequences, while the generation of long-form text remains largely underexplored. In this paper, we observe that the controllability of texts generated by the powerful prefix-based method Air-Decoding tends to decline with increasing sequence length, which we hypothesize primarily arises from the observed decay in attention to the prefixes. Meanwhile, different types of prefixes including soft and hard prefixes are also key factors influencing performance. Building on these insights, we propose a lightweight and effective framework called Dynamic Token-level Prefix Augmentation (DTPA) based on Air-Decoding for controllable text generation. Specifically, it first selects the optimal prefix type for a given task. Then we dynamically amplify the attention to the prefix for the attribute distribution to enhance controllability, with a scaling factor growing exponentially as the sequence length increases. Moreover, based on the task, we optionally apply a similar augmentation to the original prompt for the raw distribution to balance text quality. After attribute distribution reconstruction, the generated text satisfies the attribute constraints well. Experiments on multiple CTG tasks demonstrate that DTPA generally outperforms other methods in attribute control while maintaining competitive fluency, diversity, and topic relevance. Further analysis highlights DTPA's superior effectiveness in long text generation.
Enhancing Multi-hop Reasoning through Knowledge Erasure in Large Language Model Editing
Aug 22, 2024



Abstract:Large language models (LLMs) face challenges with internal knowledge inaccuracies and outdated information. Knowledge editing has emerged as a pivotal approach to mitigate these issues. Although current knowledge editing techniques exhibit promising performance in single-hop reasoning tasks, they show limitations when applied to multi-hop reasoning. Drawing on cognitive neuroscience and the operational mechanisms of LLMs, we hypothesize that the residual single-hop knowledge after editing causes edited models to revert to their original answers when processing multi-hop questions, thereby undermining their performance in multihop reasoning tasks. To validate this hypothesis, we conduct a series of experiments that empirically confirm our assumptions. Building on the validated hypothesis, we propose a novel knowledge editing method that incorporates a Knowledge Erasure mechanism for Large language model Editing (KELE). Specifically, we design an erasure function for residual knowledge and an injection function for new knowledge. Through joint optimization, we derive the optimal recall vector, which is subsequently utilized within a rank-one editing framework to update the parameters of targeted model layers. Extensive experiments on GPT-J and GPT-2 XL demonstrate that KELE substantially enhances the multi-hop reasoning capability of edited LLMs.
TraveLLM: Could you plan my new public transit route in face of a network disruption?
Jul 20, 2024



Abstract:Imagine there is a disruption in train 1 near Times Square metro station. You try to find an alternative subway route to the JFK airport on Google Maps, but the app fails to provide a suitable recommendation that takes into account the disruption and your preferences to avoid crowded stations. We find that in many such situations, current navigation apps may fall short and fail to give a reasonable recommendation. To fill this gap, in this paper, we develop a prototype, TraveLLM, to plan routing of public transit in face of disruption that relies on Large Language Models (LLMs). LLMs have shown remarkable capabilities in reasoning and planning across various domains. Here we hope to investigate the potential of LLMs that lies in incorporating multi-modal user-specific queries and constraints into public transit route recommendations. Various test cases are designed under different scenarios, including varying weather conditions, emergency events, and the introduction of new transportation services. We then compare the performance of state-of-the-art LLMs, including GPT-4, Claude 3 and Gemini, in generating accurate routes. Our comparative analysis demonstrates the effectiveness of LLMs, particularly GPT-4 in providing navigation plans. Our findings hold the potential for LLMs to enhance existing navigation systems and provide a more flexible and intelligent method for addressing diverse user needs in face of disruptions.
Learn to Tour: Operator Design For Solution Feasibility Mapping in Pickup-and-delivery Traveling Salesman Problem
Apr 17, 2024



Abstract:This paper aims to develop a learning method for a special class of traveling salesman problems (TSP), namely, the pickup-and-delivery TSP (PDTSP), which finds the shortest tour along a sequence of one-to-one pickup-and-delivery nodes. One-to-one here means that the transported people or goods are associated with designated pairs of pickup and delivery nodes, in contrast to that indistinguishable goods can be delivered to any nodes. In PDTSP, precedence constraints need to be satisfied that each pickup node must be visited before its corresponding delivery node. Classic operations research (OR) algorithms for PDTSP are difficult to scale to large-sized problems. Recently, reinforcement learning (RL) has been applied to TSPs. The basic idea is to explore and evaluate visiting sequences in a solution space. However, this approach could be less computationally efficient, as it has to potentially evaluate many infeasible solutions of which precedence constraints are violated. To restrict solution search within a feasible space, we utilize operators that always map one feasible solution to another, without spending time exploring the infeasible solution space. Such operators are evaluated and selected as policies to solve PDTSPs in an RL framework. We make a comparison of our method and baselines, including classic OR algorithms and existing learning methods. Results show that our approach can find tours shorter than baselines.
Confucius: Iterative Tool Learning from Introspection Feedback by Easy-to-Difficult Curriculum
Aug 27, 2023
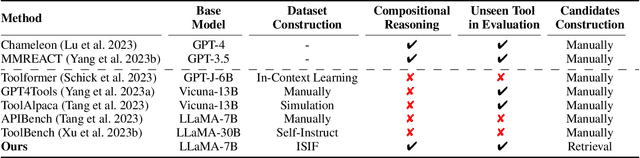
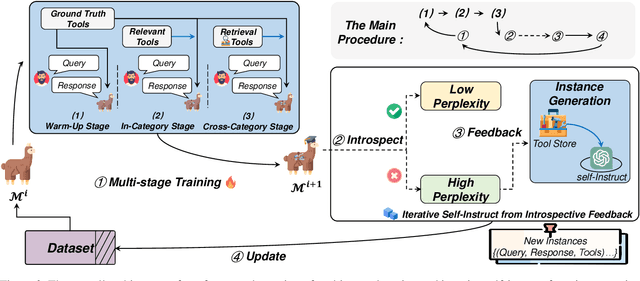

Abstract:Augmenting large language models (LLMs) with external tools has emerged as a promising approach to extending the capability of LLMs. Although some works employ open-source LLMs for the tool learning task, most of them are trained in a controlled environment in which LLMs only learn to execute the human-provided tools. However, selecting proper tools from the large toolset is also a crucial ability for the tool learning model to be applied in real-world applications. Existing methods usually directly employ self-instruction methods to train the model, which ignores differences in tool complexity. In this paper, we propose the Confucius, a novel tool learning framework to train LLM to use complicated tools in real-world scenarios, which contains two main phases: (1) We first propose a multi-stage learning method to teach the LLM to use various tools from an easy-to-difficult curriculum; (2) thenceforth, we propose the Iterative Self-instruct from Introspective Feedback (ISIF) to dynamically construct the dataset to improve the ability to use the complicated tool. Extensive experiments conducted on both controlled and real-world settings demonstrate the superiority of our tool learning framework in the real-world application scenarios compared to both tuning-free (e.g. ChatGPT, Claude) and tuning-based baselines (e.g. GPT4Tools).
A Neural RDE-based model for solving path-dependent PDEs
Jun 01, 2023



Abstract:The concept of the path-dependent partial differential equation (PPDE) was first introduced in the context of path-dependent derivatives in financial markets. Its semilinear form was later identified as a non-Markovian backward stochastic differential equation (BSDE). Compared to the classical PDE, the solution of a PPDE involves an infinite-dimensional spatial variable, making it challenging to approximate, if not impossible. In this paper, we propose a neural rough differential equation (NRDE)-based model to learn PPDEs, which effectively encodes the path information through the log-signature feature while capturing the fundamental dynamics. The proposed continuous-time model for the PPDE solution offers the benefits of efficient memory usage and the ability to scale with dimensionality. Several numerical experiments, provided to validate the performance of the proposed model in comparison to the strong baseline in the literature, are used to demonstrate its effectiveness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge