Infrequent Resolving Algorithm for Online Linear Programming

Online linear programming (OLP) has gained significant attention from both researchers and practitioners due to its extensive applications, such as online auction, network revenue management and advertising. Existing OLP algorithms fall into two categories: LP-based algorithms and LP-free algorithms. The former one typically guarantees better performance, even offering a constant regret, but requires solving a large number of LPs, which could be computationally expensive. In contrast, LP-free algorithm only requires first-order computations but induces a worse performance, lacking a constant regret bound. In this work, we bridge the gap between these two extremes by proposing an algorithm that achieves a constant regret while solving LPs only $O(\log\log T)$ times over the time horizon $T$. Moreover, when we are allowed to solve LPs only $M$ times, we propose an algorithm that can guarantee an $O\left(T^{(1/2+\epsilon)^{M-1}}\right)$ regret. Furthermore, when the arrival probabilities are known at the beginning, our algorithm can guarantee a constant regret by solving LPs $O(\log\log T)$ times, and an $O\left(T^{(1/2+\epsilon)^{M}}\right)$ regret by solving LPs only $M$ times. Numerical experiments are conducted to demonstrate the efficiency of the proposed algorithms.

ORLM: Training Large Language Models for Optimization Modeling

Large Language Models (LLMs) have emerged as powerful tools for tackling complex Operations Research (OR) problem by providing the capacity in automating optimization modeling. However, current methodologies heavily rely on prompt engineering (e.g., multi-agent cooperation) with proprietary LLMs, raising data privacy concerns that could be prohibitive in industry applications. To tackle this issue, we propose training open-source LLMs for optimization modeling. We identify four critical requirements for the training dataset of OR LLMs, design and implement OR-Instruct, a semi-automated process for creating synthetic data tailored to specific requirements. We also introduce the IndustryOR benchmark, the first industrial benchmark for testing LLMs on solving real-world OR problems. We apply the data from OR-Instruct to various open-source LLMs of 7b size (termed as ORLMs), resulting in a significantly improved capability for optimization modeling. Our best-performing ORLM achieves state-of-the-art performance on the NL4OPT, MAMO, and IndustryOR benchmarks. Our code and data are available at \url{https://github.com/Cardinal-Operations/ORLM}.

Price Interpretability of Prediction Markets: A Convergence Analysis

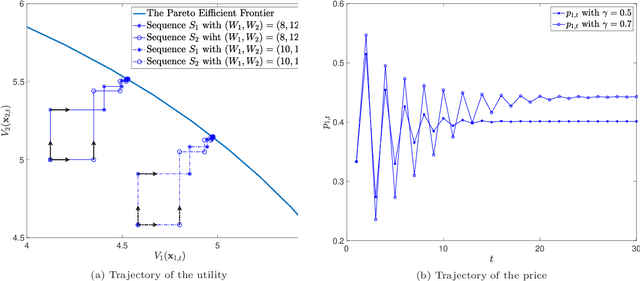
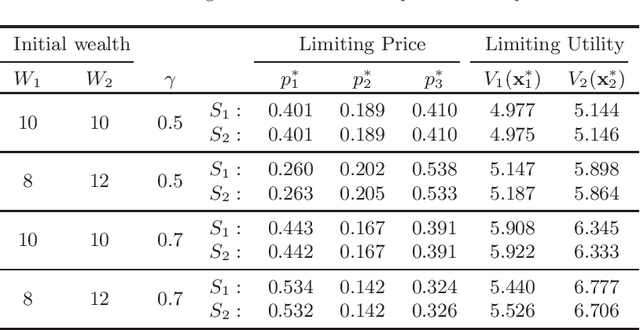
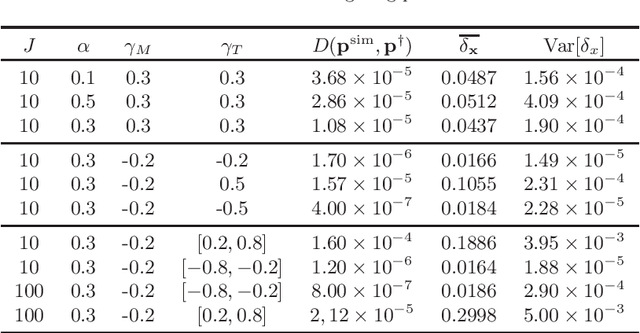
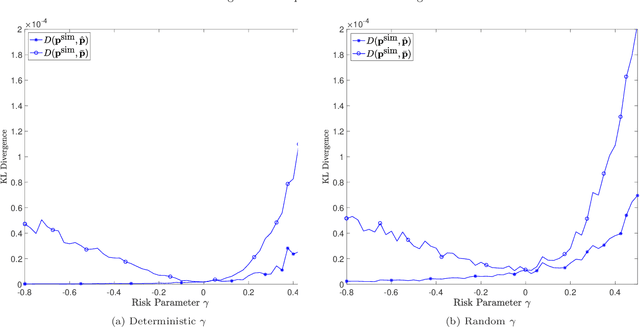
Prediction markets are long known for prediction accuracy. However, there is still a lack of systematic understanding of how prediction markets aggregate information and why they work so well. This work proposes a multivariate utility (MU)-based mechanism that unifies several existing prediction market-making schemes. Based on this mechanism, we derive convergence results for markets with myopic, risk-averse traders who repeatedly interact with the market maker. We show that the resulting limiting wealth distribution lies on the Pareto efficient frontier defined by all market participants' utilities. With the help of this result, we establish both analytical and numerical results for the limiting price for different market models. We show that the limiting price converges to the geometric mean of agents' beliefs for exponential utility-based markets. For risk measure-based markets, we construct a risk measure family that meets the convergence requirements and show that the limiting price can converge to a weighted power mean of agent beliefs. For markets based on hyperbolic absolute risk aversion (HARA) utilities, we show that the limiting price is also a risk-adjusted weighted power mean of agent beliefs, even though the trading order will affect the aggregation weights. We further propose an approximation scheme for the limiting price under the HARA utility family. We show through numerical experiments that our approximation scheme works well in predicting the convergent prices.

Random Walk Bandits

Bandit learning problems find important applications ranging from medical trials to online advertisement. In this paper, we study a novel bandit learning problem motivated by recommender systems. The goal is to recommend items so that users are likely to continue browsing. Our model views a user's browsing record as a random walk over a graph of webpages. This random walk ends (hits an absorbing node) when the user exits the website. Our model introduces a novel learning problem that calls for new technical insights on learning with graph random walk feedback. In particular, the performance and complexity depend on the structure of the decision space (represented by graphs). Our paper provides a comprehensive understanding of this new problem. We provide bandit learning algorithms for this problem with provable performance guarantees, and provide matching lower bounds.

Probabilistic Forecasting with Temporal Convolutional Neural Network

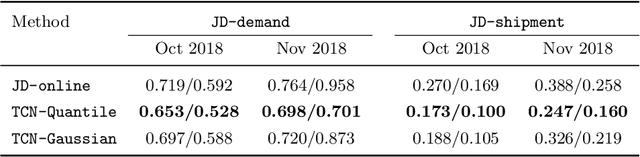
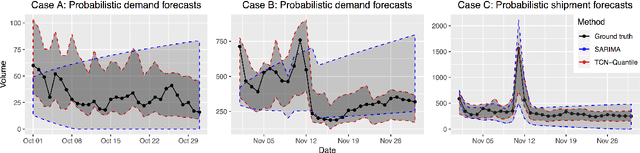
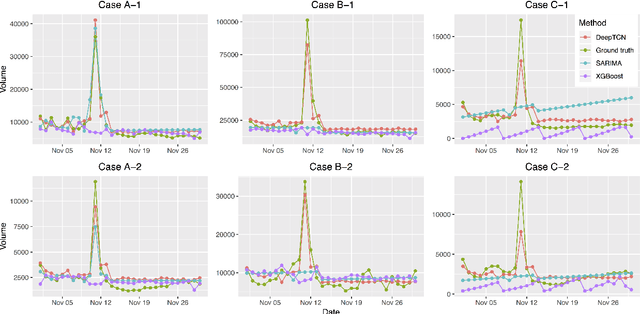
We present a probabilistic forecasting framework based on convolutional neural network for multiple related time series forecasting. The framework can be applied to estimate probability density under both parametric and non-parametric settings. More specifically, stacked residual blocks based on dilated causal convolutional nets are constructed to capture the temporal dependencies of the series. Combined with representation learning, our approach is able to learn complex patterns such as seasonality, holiday effects within and across series, and to leverage those patterns for more accurate forecasts, especially when historical data is sparse or unavailable. Extensive empirical studies are performed on several real-world datasets, including datasets from JD.com, China's largest online retailer. The results show that our framework outperforms other state-of-the-art methods in both accuracy and efficiency.

A Near-Optimal Dynamic Learning Algorithm for Online Matching Problems with Concave Returns

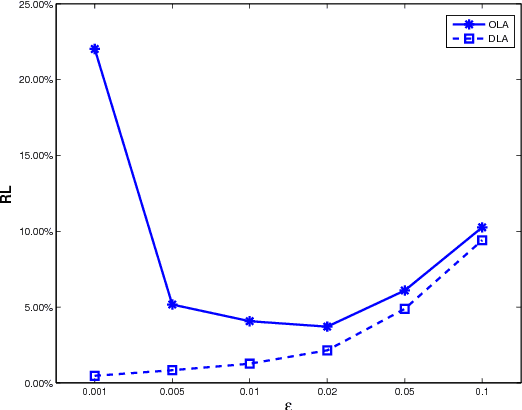
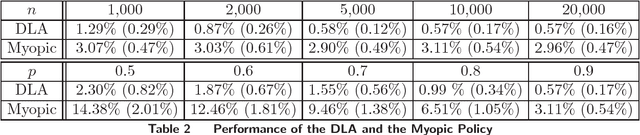
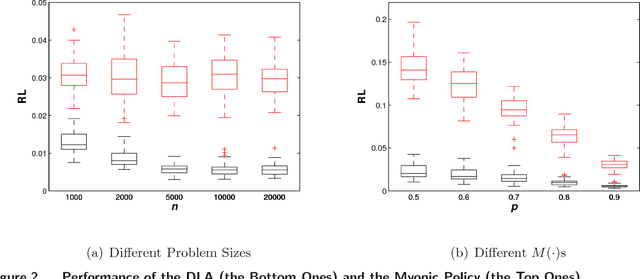
We consider an online matching problem with concave returns. This problem is a significant generalization of the Adwords allocation problem and has vast applications in online advertising. In this problem, a sequence of items arrive sequentially and each has to be allocated to one of the bidders, who bid a certain value for each item. At each time, the decision maker has to allocate the current item to one of the bidders without knowing the future bids and the objective is to maximize the sum of some concave functions of each bidder's aggregate value. In this work, we propose an algorithm that achieves near-optimal performance for this problem when the bids arrive in a random order and the input data satisfies certain conditions. The key idea of our algorithm is to learn the input data pattern dynamically: we solve a sequence of carefully chosen partial allocation problems and use their optimal solutions to assist with the future decision. Our analysis belongs to the primal-dual paradigm, however, the absence of linearity of the objective function and the dynamic feature of the algorithm makes our analysis quite unique.

A Dynamic Near-Optimal Algorithm for Online Linear Programming

A natural optimization model that formulates many online resource allocation and revenue management problems is the online linear program (LP) in which the constraint matrix is revealed column by column along with the corresponding objective coefficient. In such a model, a decision variable has to be set each time a column is revealed without observing the future inputs and the goal is to maximize the overall objective function. In this paper, we provide a near-optimal algorithm for this general class of online problems under the assumption of random order of arrival and some mild conditions on the size of the LP right-hand-side input. Specifically, our learning-based algorithm works by dynamically updating a threshold price vector at geometric time intervals, where the dual prices learned from the revealed columns in the previous period are used to determine the sequential decisions in the current period. Due to the feature of dynamic learning, the competitiveness of our algorithm improves over the past study of the same problem. We also present a worst-case example showing that the performance of our algorithm is near-optimal.

Close the Gaps: A Learning-while-Doing Algorithm for a Class of Single-Product Revenue Management Problems

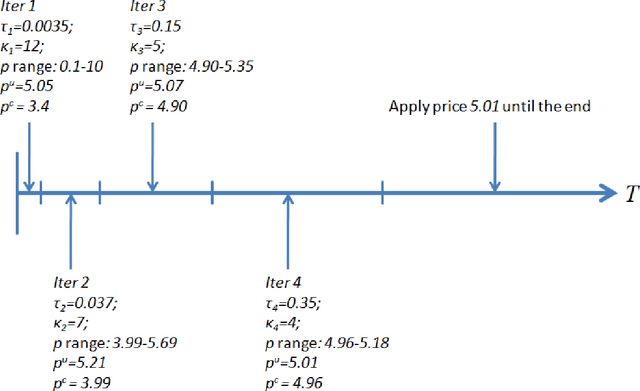
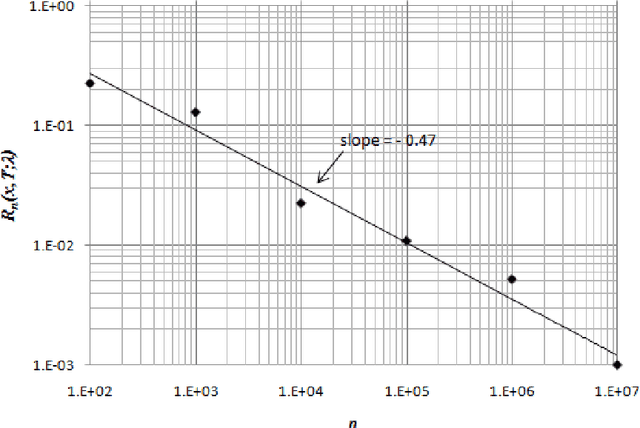
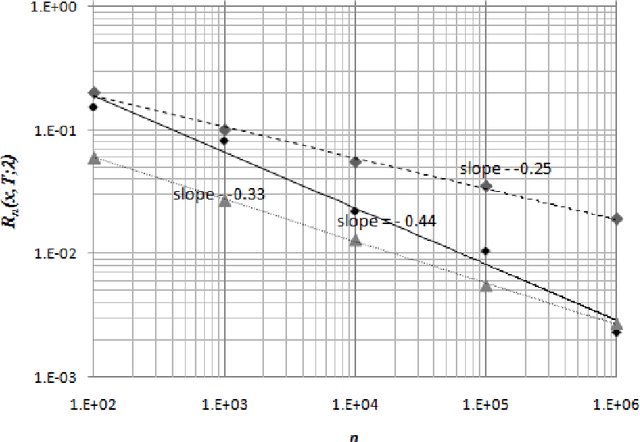
We consider a retailer selling a single product with limited on-hand inventory over a finite selling season. Customer demand arrives according to a Poisson process, the rate of which is influenced by a single action taken by the retailer (such as price adjustment, sales commission, advertisement intensity, etc.). The relationship between the action and the demand rate is not known in advance. However, the retailer is able to learn the optimal action "on the fly" as she maximizes her total expected revenue based on the observed demand reactions. Using the pricing problem as an example, we propose a dynamic "learning-while-doing" algorithm that only involves function value estimation to achieve a near-optimal performance. Our algorithm employs a series of shrinking price intervals and iteratively tests prices within that interval using a set of carefully chosen parameters. We prove that the convergence rate of our algorithm is among the fastest of all possible algorithms in terms of asymptotic "regret" (the relative loss comparing to the full information optimal solution). Our result closes the performance gaps between parametric and non-parametric learning and between a post-price mechanism and a customer-bidding mechanism. Important managerial insight from this research is that the values of information on both the parametric form of the demand function as well as each customer's exact reservation price are less important than prior literature suggests. Our results also suggest that firms would be better off to perform dynamic learning and action concurrently rather than sequentially.