Price Interpretability of Prediction Markets: A Convergence Analysis
Paper and Code
May 18, 2022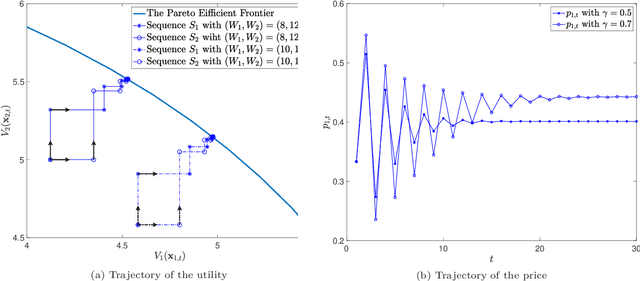
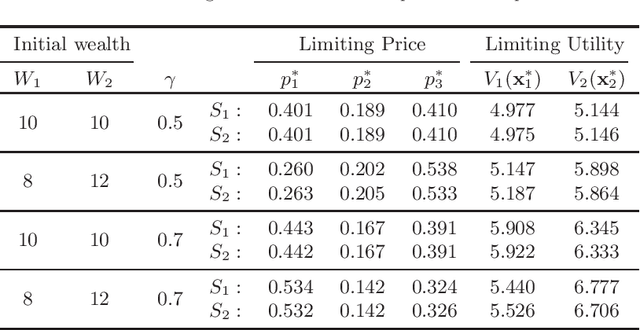
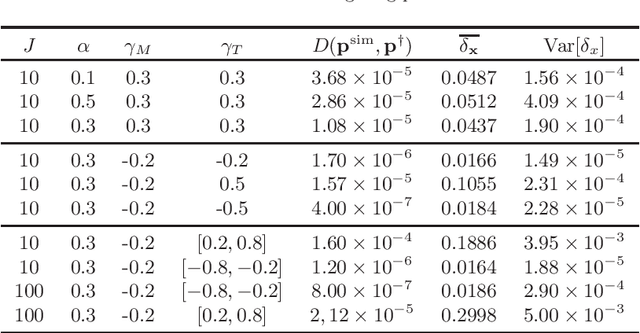
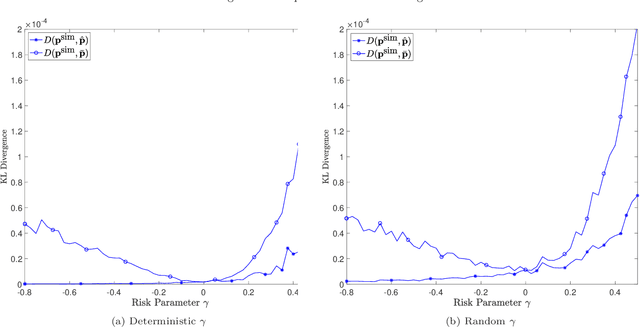
Prediction markets are long known for prediction accuracy. However, there is still a lack of systematic understanding of how prediction markets aggregate information and why they work so well. This work proposes a multivariate utility (MU)-based mechanism that unifies several existing prediction market-making schemes. Based on this mechanism, we derive convergence results for markets with myopic, risk-averse traders who repeatedly interact with the market maker. We show that the resulting limiting wealth distribution lies on the Pareto efficient frontier defined by all market participants' utilities. With the help of this result, we establish both analytical and numerical results for the limiting price for different market models. We show that the limiting price converges to the geometric mean of agents' beliefs for exponential utility-based markets. For risk measure-based markets, we construct a risk measure family that meets the convergence requirements and show that the limiting price can converge to a weighted power mean of agent beliefs. For markets based on hyperbolic absolute risk aversion (HARA) utilities, we show that the limiting price is also a risk-adjusted weighted power mean of agent beliefs, even though the trading order will affect the aggregation weights. We further propose an approximation scheme for the limiting price under the HARA utility family. We show through numerical experiments that our approximation scheme works well in predicting the convergent prices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge