A Near-Optimal Dynamic Learning Algorithm for Online Matching Problems with Concave Returns

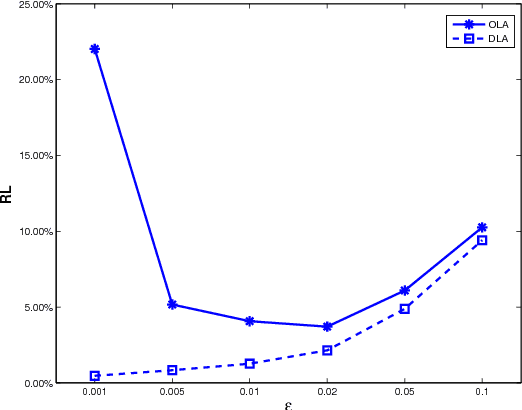
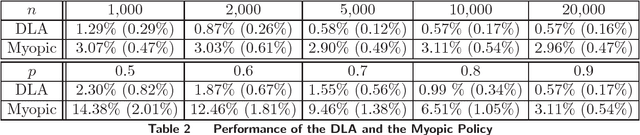
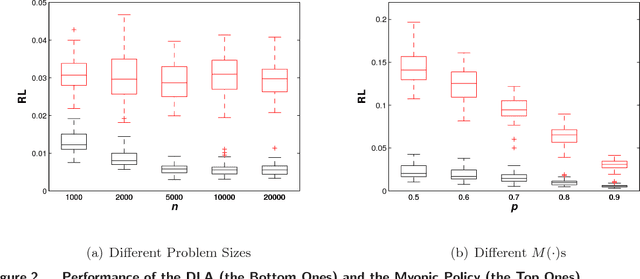
We consider an online matching problem with concave returns. This problem is a significant generalization of the Adwords allocation problem and has vast applications in online advertising. In this problem, a sequence of items arrive sequentially and each has to be allocated to one of the bidders, who bid a certain value for each item. At each time, the decision maker has to allocate the current item to one of the bidders without knowing the future bids and the objective is to maximize the sum of some concave functions of each bidder's aggregate value. In this work, we propose an algorithm that achieves near-optimal performance for this problem when the bids arrive in a random order and the input data satisfies certain conditions. The key idea of our algorithm is to learn the input data pattern dynamically: we solve a sequence of carefully chosen partial allocation problems and use their optimal solutions to assist with the future decision. Our analysis belongs to the primal-dual paradigm, however, the absence of linearity of the objective function and the dynamic feature of the algorithm makes our analysis quite unique.