Everywhere Valid Bounds on False Discovery Proportions in Conformal Inference

Modern applications of conformal inference to multiple testing problems, such as outlier detection and candidate selection, often involve selecting test samples whose conformal p-values fall below a threshold. The quality of such methods is often measured by the false discovery proportion (FDP), defined as the fraction of incorrect selections. Existing approaches typically control the expected value of the FDP, using methods such as the Benjamini-Hochberg procedure. This approach fails to provide high-probability bounds on the realized false discovery proportion and invalidates statistical guarantees if the rejection threshold is selected after inspecting the data. This paper establishes finite-sample, distribution-free upper bounds on the FDP that hold simultaneously over all possible rejection thresholds, enabling arbitrary post hoc selection of the threshold. Simultaneous validity is achieved by constructing a high-probability envelope for the empirical distribution function of null conformal p-values by sampling from their joint distribution. Furthermore, our framework allows practitioners to modulate the envelope's shape, thereby producing tight bounds in rejection regions of primary interest. We use this flexible approach to derive simultaneous FDP upper bounds for both outlier detection and conformal selection. We demonstrate through synthetic and real-data experiments that the resulting bounds are both valid and substantially less conservative than those derived from existing approaches.

Emerging Properties in Unified Multimodal Pretraining

Unifying multimodal understanding and generation has shown impressive capabilities in cutting-edge proprietary systems. In this work, we introduce BAGEL, an open0source foundational model that natively supports multimodal understanding and generation. BAGEL is a unified, decoder0only model pretrained on trillions of tokens curated from large0scale interleaved text, image, video, and web data. When scaled with such diverse multimodal interleaved data, BAGEL exhibits emerging capabilities in complex multimodal reasoning. As a result, it significantly outperforms open-source unified models in both multimodal generation and understanding across standard benchmarks, while exhibiting advanced multimodal reasoning abilities such as free-form image manipulation, future frame prediction, 3D manipulation, and world navigation. In the hope of facilitating further opportunities for multimodal research, we share the key findings, pretraining details, data creation protocal, and release our code and checkpoints to the community. The project page is at https://bagel-ai.org/

MoE-Pruner: Pruning Mixture-of-Experts Large Language Model using the Hints from Its Router

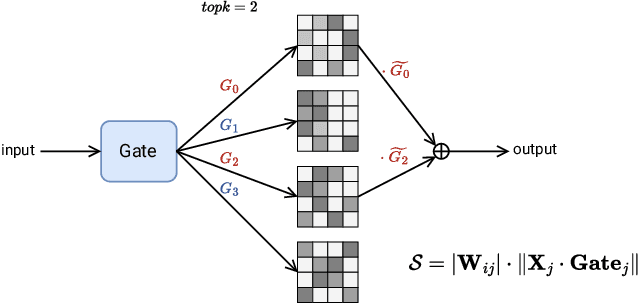
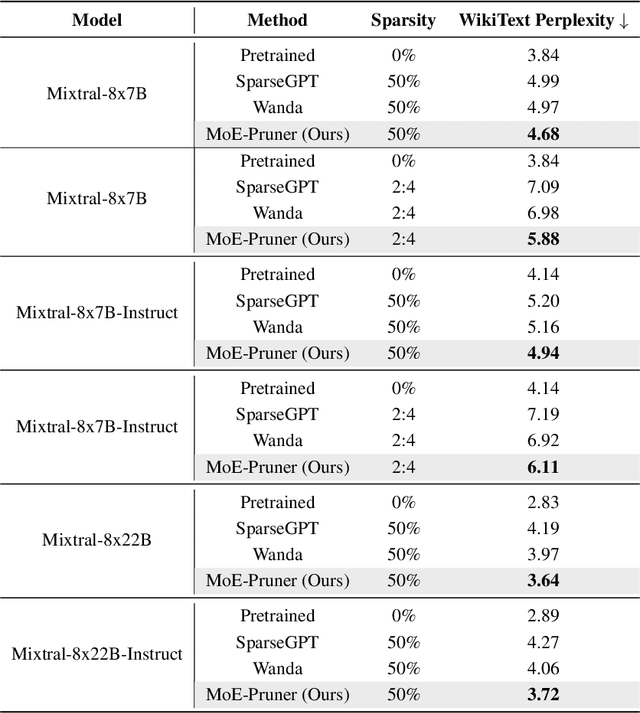
Mixture-of-Experts (MoE) architectures face challenges such as high memory consumption and redundancy in experts. Pruning MoE can reduce network weights while maintaining model performance. Motivated by the recent observation of emergent large magnitude features in Large Language Models (LLM) and MoE routing policy, we propose MoE-Pruner, a method that prunes weights with the smallest magnitudes multiplied by the corresponding input activations and router weights, on each output neuron. Our pruning method is one-shot, requiring no retraining or weight updates. We evaluate our method on Mixtral-8x7B and Mixtral-8x22B across multiple language benchmarks. Experimental results show that our pruning method significantly outperforms state-of-the-art LLM pruning methods. Furthermore, our pruned MoE models can benefit from a pretrained teacher model through expert-wise knowledge distillation, improving performance post-pruning. Experimental results demonstrate that the Mixtral-8x7B model with 50% sparsity maintains 99% of the performance of the original model after the expert-wise knowledge distillation.

Reward Collapse in Aligning Large Language Models

The extraordinary capabilities of large language models (LLMs) such as ChatGPT and GPT-4 are in part unleashed by aligning them with reward models that are trained on human preferences, which are often represented as rankings of responses to prompts. In this paper, we document the phenomenon of \textit{reward collapse}, an empirical observation where the prevailing ranking-based approach results in an \textit{identical} reward distribution \textit{regardless} of the prompts during the terminal phase of training. This outcome is undesirable as open-ended prompts like ``write a short story about your best friend'' should yield a continuous range of rewards for their completions, while specific prompts like ``what is the capital of New Zealand'' should generate either high or low rewards. Our theoretical investigation reveals that reward collapse is primarily due to the insufficiency of the ranking-based objective function to incorporate prompt-related information during optimization. This insight allows us to derive closed-form expressions for the reward distribution associated with a set of utility functions in an asymptotic regime. To overcome reward collapse, we introduce a prompt-aware optimization scheme that provably admits a prompt-dependent reward distribution within the interpolating regime. Our experimental results suggest that our proposed prompt-aware utility functions significantly alleviate reward collapse during the training of reward models.

Efficient $Φ$-Regret Minimization in Extensive-Form Games via Online Mirror Descent

A conceptually appealing approach for learning Extensive-Form Games (EFGs) is to convert them to Normal-Form Games (NFGs). This approach enables us to directly translate state-of-the-art techniques and analyses in NFGs to learning EFGs, but typically suffers from computational intractability due to the exponential blow-up of the game size introduced by the conversion. In this paper, we address this problem in natural and important setups for the \emph{$\Phi$-Hedge} algorithm -- A generic algorithm capable of learning a large class of equilibria for NFGs. We show that $\Phi$-Hedge can be directly used to learn Nash Equilibria (zero-sum settings), Normal-Form Coarse Correlated Equilibria (NFCCE), and Extensive-Form Correlated Equilibria (EFCE) in EFGs. We prove that, in those settings, the \emph{$\Phi$-Hedge} algorithms are equivalent to standard Online Mirror Descent (OMD) algorithms for EFGs with suitable dilated regularizers, and run in polynomial time. This new connection further allows us to design and analyze a new class of OMD algorithms based on modifying its log-partition function. In particular, we design an improved algorithm with balancing techniques that achieves a sharp $\widetilde{\mathcal{O}}(\sqrt{XAT})$ EFCE-regret under bandit-feedback in an EFG with $X$ information sets, $A$ actions, and $T$ episodes. To our best knowledge, this is the first such rate and matches the information-theoretic lower bound.

Sample-Efficient Learning of Correlated Equilibria in Extensive-Form Games

Imperfect-Information Extensive-Form Games (IIEFGs) is a prevalent model for real-world games involving imperfect information and sequential plays. The Extensive-Form Correlated Equilibrium (EFCE) has been proposed as a natural solution concept for multi-player general-sum IIEFGs. However, existing algorithms for finding an EFCE require full feedback from the game, and it remains open how to efficiently learn the EFCE in the more challenging bandit feedback setting where the game can only be learned by observations from repeated playing. This paper presents the first sample-efficient algorithm for learning the EFCE from bandit feedback. We begin by proposing $K$-EFCE -- a more generalized definition that allows players to observe and deviate from the recommended actions for $K$ times. The $K$-EFCE includes the EFCE as a special case at $K=1$, and is an increasingly stricter notion of equilibrium as $K$ increases. We then design an uncoupled no-regret algorithm that finds an $\varepsilon$-approximate $K$-EFCE within $\widetilde{\mathcal{O}}(\max_{i}X_iA_i^{K}/\varepsilon^2)$ iterations in the full feedback setting, where $X_i$ and $A_i$ are the number of information sets and actions for the $i$-th player. Our algorithm works by minimizing a wide-range regret at each information set that takes into account all possible recommendation histories. Finally, we design a sample-based variant of our algorithm that learns an $\varepsilon$-approximate $K$-EFCE within $\widetilde{\mathcal{O}}(\max_{i}X_iA_i^{K+1}/\varepsilon^2)$ episodes of play in the bandit feedback setting. When specialized to $K=1$, this gives the first sample-efficient algorithm for learning EFCE from bandit feedback.

Learn To Remember: Transformer with Recurrent Memory for Document-Level Machine Translation

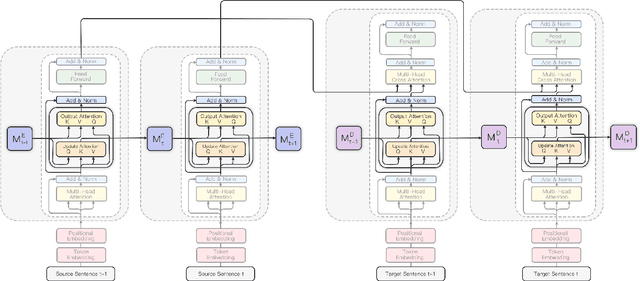
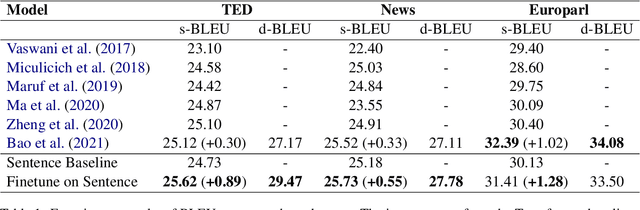
The Transformer architecture has led to significant gains in machine translation. However, most studies focus on only sentence-level translation without considering the context dependency within documents, leading to the inadequacy of document-level coherence. Some recent research tried to mitigate this issue by introducing an additional context encoder or translating with multiple sentences or even the entire document. Such methods may lose the information on the target side or have an increasing computational complexity as documents get longer. To address such problems, we introduce a recurrent memory unit to the vanilla Transformer, which supports the information exchange between the sentence and previous context. The memory unit is recurrently updated by acquiring information from sentences, and passing the aggregated knowledge back to subsequent sentence states. We follow a two-stage training strategy, in which the model is first trained at the sentence level and then finetuned for document-level translation. We conduct experiments on three popular datasets for document-level machine translation and our model has an average improvement of 0.91 s-BLEU over the sentence-level baseline. We also achieve state-of-the-art results on TED and News, outperforming the previous work by 0.36 s-BLEU and 1.49 d-BLEU on average.

When Can We Learn General-Sum Markov Games with a Large Number of Players Sample-Efficiently?

Multi-agent reinforcement learning has made substantial empirical progresses in solving games with a large number of players. However, theoretically, the best known sample complexity for finding a Nash equilibrium in general-sum games scales exponentially in the number of players due to the size of the joint action space, and there is a matching exponential lower bound. This paper investigates what learning goals admit better sample complexities in the setting of $m$-player general-sum Markov games with $H$ steps, $S$ states, and $A_i$ actions per player. First, we design algorithms for learning an $\epsilon$-Coarse Correlated Equilibrium (CCE) in $\widetilde{\mathcal{O}}(H^5S\max_{i\le m} A_i / \epsilon^2)$ episodes, and an $\epsilon$-Correlated Equilibrium (CE) in $\widetilde{\mathcal{O}}(H^6S\max_{i\le m} A_i^2 / \epsilon^2)$ episodes. This is the first line of results for learning CCE and CE with sample complexities polynomial in $\max_{i\le m} A_i$. Our algorithm for learning CE integrates an adversarial bandit subroutine which minimizes a weighted swap regret, along with several novel designs in the outer loop. Second, we consider the important special case of Markov Potential Games, and design an algorithm that learns an $\epsilon$-approximate Nash equilibrium within $\widetilde{\mathcal{O}}(S\sum_{i\le m} A_i / \epsilon^3)$ episodes (when only highlighting the dependence on $S$, $A_i$, and $\epsilon$), which only depends linearly in $\sum_{i\le m} A_i$ and significantly improves over the best known algorithm in the $\epsilon$ dependence. Overall, our results shed light on what equilibria or structural assumptions on the game may enable sample-efficient learning with many players.