InternLM2.5-StepProver: Advancing Automated Theorem Proving via Expert Iteration on Large-Scale LEAN Problems

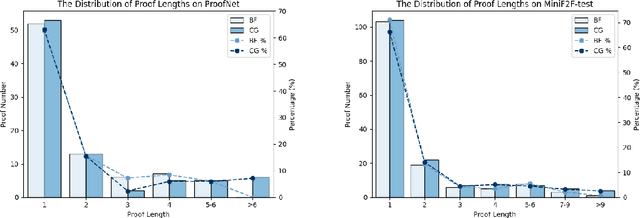
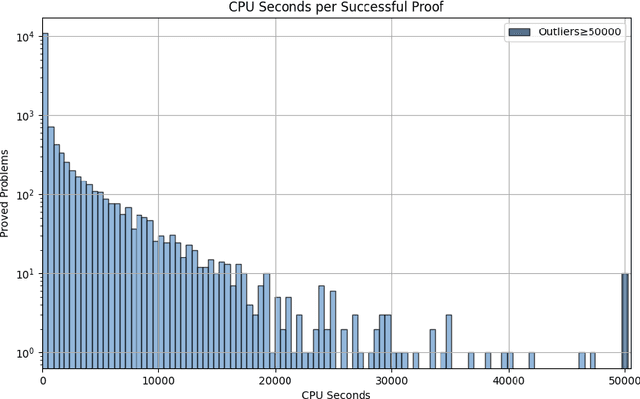
Large Language Models (LLMs) have emerged as powerful tools in mathematical theorem proving, particularly when utilizing formal languages such as LEAN. The major learning paradigm is expert iteration, which necessitates a pre-defined dataset comprising numerous mathematical problems. In this process, LLMs attempt to prove problems within the dataset and iteratively refine their capabilities through self-training on the proofs they discover. We propose to use large scale LEAN problem datasets Lean-workbook for expert iteration with more than 20,000 CPU days. During expert iteration, we found log-linear trends between solved problem amount with proof length and CPU usage. We train a critic model to select relatively easy problems for policy models to make trials and guide the model to search for deeper proofs. InternLM2.5-StepProver achieves open-source state-of-the-art on MiniF2F, Lean-Workbook-Plus, ProofNet, and Putnam benchmarks. Specifically, it achieves a pass of 65.9% on the MiniF2F-test and proves (or disproves) 17.0% of problems in Lean-Workbook-Plus which shows a significant improvement compared to only 9.5% of problems proved when Lean-Workbook-Plus was released. We open-source our models and searched proofs at https://github.com/InternLM/InternLM-Math and https://huggingface.co/datasets/internlm/Lean-Workbook.

Scaling Behavior for Large Language Models regarding Numeral Systems: An Example using Pythia

Though Large Language Models (LLMs) have shown remarkable abilities in mathematics reasoning, they are still struggling with performing numeric operations accurately, such as addition and multiplication. Numbers can be tokenized into tokens in various ways by different LLMs and affect the numeric operations performance. Currently, there are two representatives: 1) Tokenize into $1$-digit, and 2) Tokenize into $1\sim 3$ digit. The difference is roughly equivalent to using different numeral systems (namely base $10$ or base $10^{3}$). In light of this, we study the scaling behavior of different numeral systems in the context of transformer-based large language models. We empirically show that a base $10$ system is consistently more data-efficient than a base $10^{2}$ or $10^{3}$ system across training data scale, model sizes under from-scratch training settings, while different number systems have very similar fine-tuning performances. We attribute this to higher token frequencies of a base $10$ system. Additionally, we reveal extrapolation behavior patterns on addition and multiplication. We identify that base $100$ and base $1000$ systems struggle on token-level discernment and token-level operations. We also sheds light on the mechanism learnt by the models.

StackSight: Unveiling WebAssembly through Large Language Models and Neurosymbolic Chain-of-Thought Decompilation

WebAssembly enables near-native execution in web applications and is increasingly adopted for tasks that demand high performance and robust security. However, its assembly-like syntax, implicit stack machine, and low-level data types make it extremely difficult for human developers to understand, spurring the need for effective WebAssembly reverse engineering techniques. In this paper, we propose StackSight, a novel neurosymbolic approach that combines Large Language Models (LLMs) with advanced program analysis to decompile complex WebAssembly code into readable C++ snippets. StackSight visualizes and tracks virtual stack alterations via a static analysis algorithm and then applies chain-of-thought prompting to harness LLM's complex reasoning capabilities. Evaluation results show that StackSight significantly improves WebAssembly decompilation. Our user study also demonstrates that code snippets generated by StackSight have significantly higher win rates and enable a better grasp of code semantics.

InternLM-Math: Open Math Large Language Models Toward Verifiable Reasoning

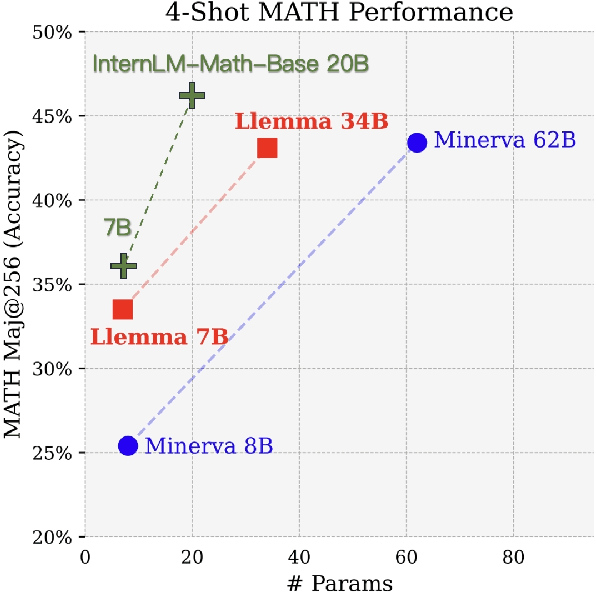
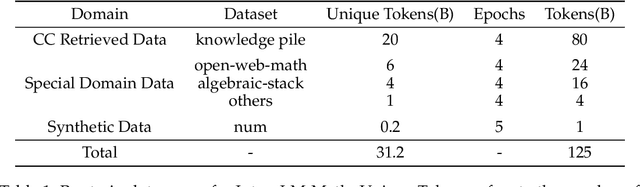
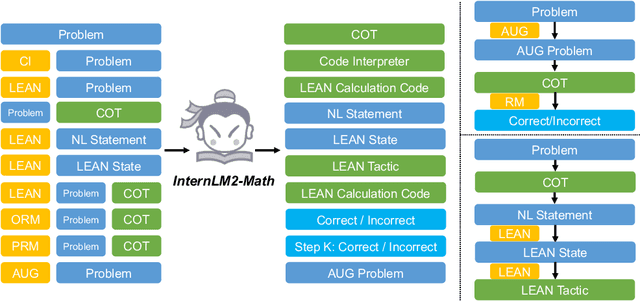
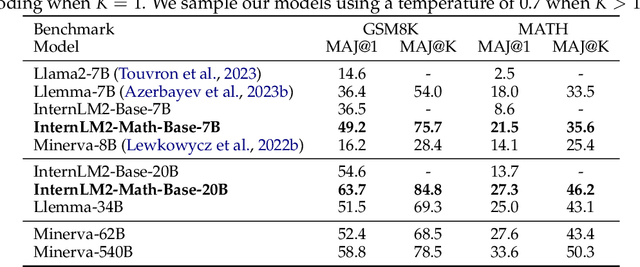
The math abilities of large language models can represent their abstract reasoning ability. In this paper, we introduce and open-source our math reasoning LLMs InternLM-Math which is continue pre-trained from InternLM2. We unify chain-of-thought reasoning, reward modeling, formal reasoning, data augmentation, and code interpreter in a unified seq2seq format and supervise our model to be a versatile math reasoner, verifier, prover, and augmenter. These abilities can be used to develop the next math LLMs or self-iteration. InternLM-Math obtains open-sourced state-of-the-art performance under the setting of in-context learning, supervised fine-tuning, and code-assisted reasoning in various informal and formal benchmarks including GSM8K, MATH, Hungary math exam, MathBench-ZH, and MiniF2F. Our pre-trained model achieves 30.3 on the MiniF2F test set without fine-tuning. We further explore how to use LEAN to solve math problems and study its performance under the setting of multi-task learning which shows the possibility of using LEAN as a unified platform for solving and proving in math. Our models, codes, and data are released at \url{https://github.com/InternLM/InternLM-Math}.

ConFiguRe: Exploring Discourse-level Chinese Figures of Speech

Figures of speech, such as metaphor and irony, are ubiquitous in literature works and colloquial conversations. This poses great challenge for natural language understanding since figures of speech usually deviate from their ostensible meanings to express deeper semantic implications. Previous research lays emphasis on the literary aspect of figures and seldom provide a comprehensive exploration from a view of computational linguistics. In this paper, we first propose the concept of figurative unit, which is the carrier of a figure. Then we select 12 types of figures commonly used in Chinese, and build a Chinese corpus for Contextualized Figure Recognition (ConFiguRe). Different from previous token-level or sentence-level counterparts, ConFiguRe aims at extracting a figurative unit from discourse-level context, and classifying the figurative unit into the right figure type. On ConFiguRe, three tasks, i.e., figure extraction, figure type classification and figure recognition, are designed and the state-of-the-art techniques are utilized to implement the benchmarks. We conduct thorough experiments and show that all three tasks are challenging for existing models, thus requiring further research. Our dataset and code are publicly available at https://github.com/pku-tangent/ConFiguRe.