Zach Shahn
Estimating heterogeneous treatment effect from survival outcomes via (orthogonal) censoring unbiased learning
Jan 20, 2024Abstract:Methods for estimating heterogeneous treatment effects (HTE) from observational data have largely focused on continuous or binary outcomes, with less attention paid to survival outcomes and almost none to settings with competing risks. In this work, we develop censoring unbiased transformations (CUTs) for survival outcomes both with and without competing risks.After converting time-to-event outcomes using these CUTs, direct application of HTE learners for continuous outcomes yields consistent estimates of heterogeneous cumulative incidence effects, total effects, and separable direct effects. Our CUTs enable application of a much larger set of state of the art HTE learners for censored outcomes than had previously been available, especially in competing risks settings. We provide generic model-free learner-specific oracle inequalities bounding the finite-sample excess risk. The oracle efficiency results depend on the oracle selector and estimated nuisance functions from all steps involved in the transformation. We demonstrate the empirical performance of the proposed methods in simulation studies.
Efficient estimation of weighted cumulative treatment effects by double/debiased machine learning
May 03, 2023Abstract:In empirical studies with time-to-event outcomes, investigators often leverage observational data to conduct causal inference on the effect of exposure when randomized controlled trial data is unavailable. Model misspecification and lack of overlap are common issues in observational studies, and they often lead to inconsistent and inefficient estimators of the average treatment effect. Estimators targeting overlap weighted effects have been proposed to address the challenge of poor overlap, and methods enabling flexible machine learning for nuisance models address model misspecification. However, the approaches that allow machine learning for nuisance models have not been extended to the setting of weighted average treatment effects for time-to-event outcomes when there is poor overlap. In this work, we propose a class of one-step cross-fitted double/debiased machine learning estimators for the weighted cumulative causal effect as a function of restriction time. We prove that the proposed estimators are consistent, asymptotically linear, and reach semiparametric efficiency bounds under regularity conditions. Our simulations show that the proposed estimators using nonparametric machine learning nuisance models perform as well as established methods that require correctly-specified parametric nuisance models, illustrating that our estimators mitigate the need for oracle parametric nuisance models. We apply the proposed methods to real-world observational data from a UK primary care database to compare the effects of anti-diabetic drugs on cancer clinical outcomes.
Blending Knowledge in Deep Recurrent Networks for Adverse Event Prediction at Hospital Discharge
Apr 09, 2021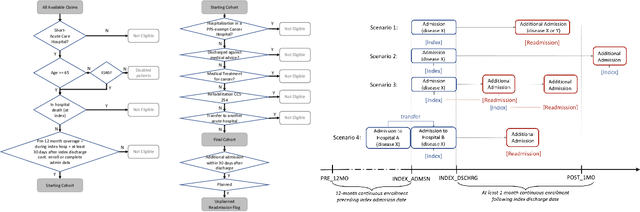
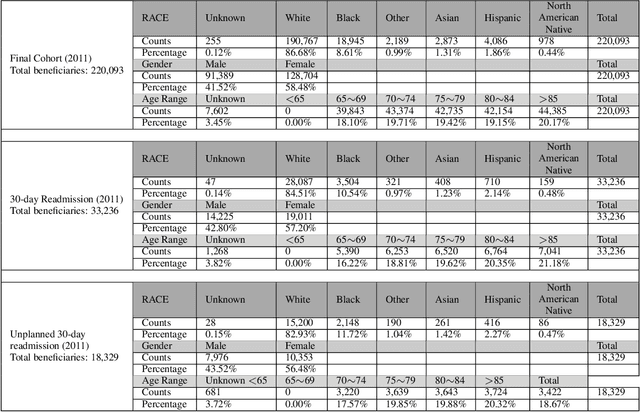
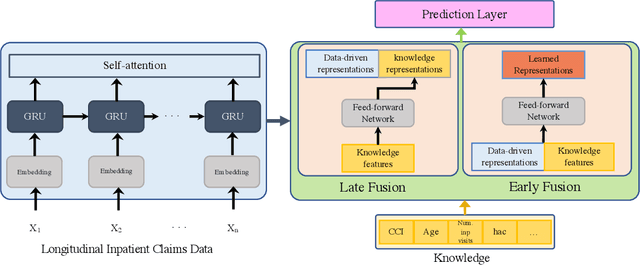

Abstract:Deep learning architectures have an extremely high-capacity for modeling complex data in a wide variety of domains. However, these architectures have been limited in their ability to support complex prediction problems using insurance claims data, such as readmission at 30 days, mainly due to data sparsity issue. Consequently, classical machine learning methods, especially those that embed domain knowledge in handcrafted features, are often on par with, and sometimes outperform, deep learning approaches. In this paper, we illustrate how the potential of deep learning can be achieved by blending domain knowledge within deep learning architectures to predict adverse events at hospital discharge, including readmissions. More specifically, we introduce a learning architecture that fuses a representation of patient data computed by a self-attention based recurrent neural network, with clinically relevant features. We conduct extensive experiments on a large claims dataset and show that the blended method outperforms the standard machine learning approaches.
G-Net: A Deep Learning Approach to G-computation for Counterfactual Outcome Prediction Under Dynamic Treatment Regimes
Mar 23, 2020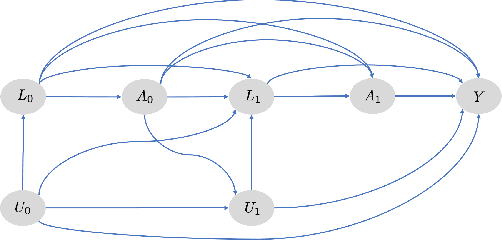

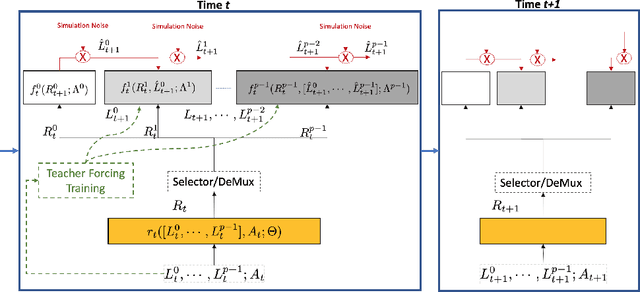
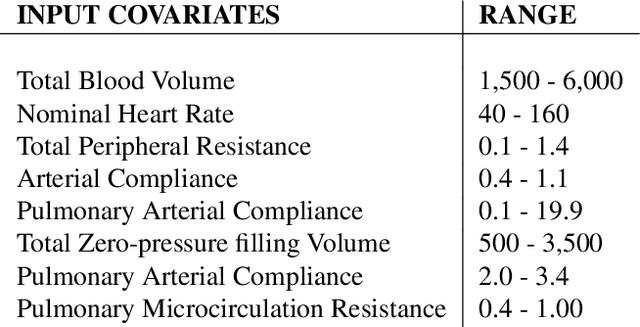
Abstract:Counterfactual prediction is a fundamental task in decision-making. G-computation is a method for estimating expected counterfactual outcomes under dynamic time-varying treatment strategies. Existing G-computation implementations have mostly employed classical regression models with limited capacity to capture complex temporal and nonlinear dependence structures. This paper introduces G-Net, a novel sequential deep learning framework for G-computation that can handle complex time series data while imposing minimal modeling assumptions and provide estimates of individual or population-level time varying treatment effects. We evaluate alternative G-Net implementations using realistically complex temporal simulated data obtained from CVSim, a mechanistic model of the cardiovascular system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge