Low-Interference Near-Field Multi-User Communication Enabled by Spatially Converging Multi-Mode Vortex Waves

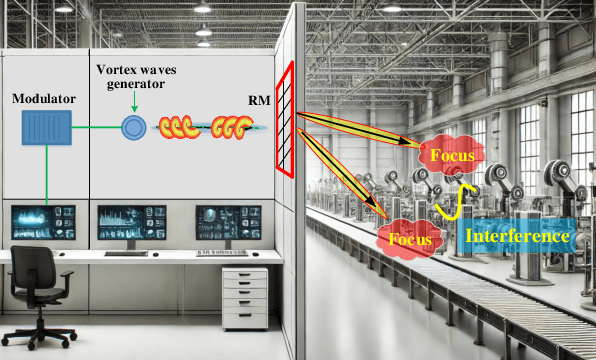
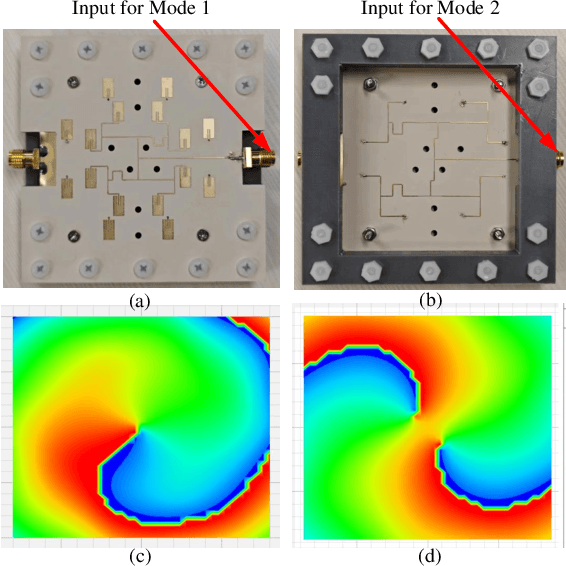
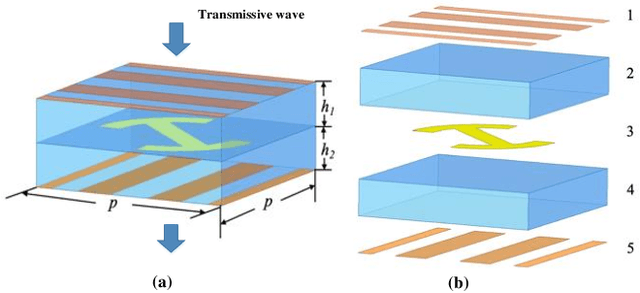
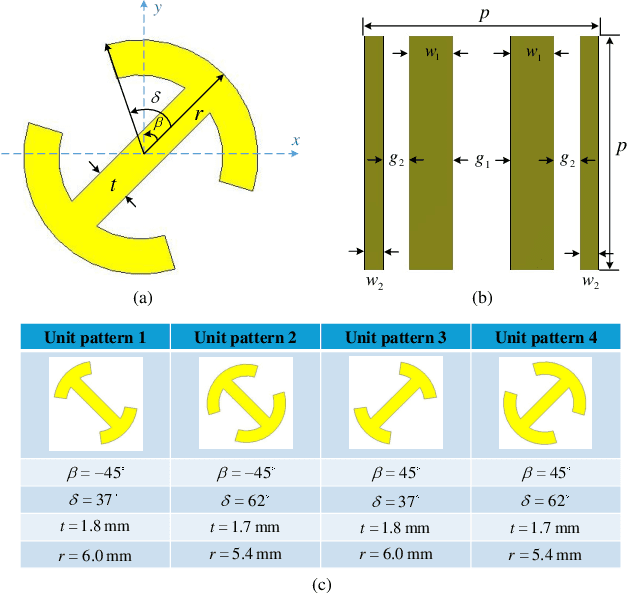
This paper proposes a multi-user Spatial Division Multiplexing (SDM) near-field access scheme, inspired by the orthogonal characteristics of multi-mode vortex waves. A Reconfigurable Meta-surface (RM) is ingeniously employed as the gateway for information transmission. This RM not only receives spatially overlapping multiplexed multi-mode vortex beams but also converts them into focused point beams in the near field. Specifically, a multi-port microstrip array method is utilized to generate multiple orthogonal vortex electromagnetic wave modes. Different ports serve as feeding points for baseband signals, allowing independent modulated data to be flexibly loaded onto different modes. After being adjusted by the RM, the vortex electromagnetic waves are converted into energy-focusing point beams, which can be directed to arbitrary 3D positions in the RM's near-field region and received by different users. Since the spatial positions of the point beams are non-overlapping, this approach not only ensures energy concentration but also significantly reduces inter-user interference. Near-field scanning results in a microwave anechoic chamber validate the effectiveness of this method, while real-time communication demonstrations confirm the system's capability for low-interference information multiplexing and transmission in practical scenarios.

Harnessing Rydberg Atomic Receivers: From Quantum Physics to Wireless Communications

The intrinsic integration of Rydberg atomic receivers into wireless communication systems is proposed, by harnessing the principles of quantum physics in wireless communications. More particularly, we conceive a pair of Rydberg atomic receivers, one incorporates a local oscillator (LO), referred to as an LO-dressed receiver, while the other operates without an LO and is termed an LO-free receiver. The appropriate wireless model is developed for each configuration, elaborating on the receiver's responses to the radio frequency (RF) signal, on the potential noise sources, and on the system performance. Next, we investigate the association distortion effects that might occur, specifically demonstrating the boundaries of linear dynamic regions, which provides critical insights into its practical implementations in wireless systems. Extensive simulation results are provided for characterizing the performance of wireless systems, harnessing this pair of Rydberg atomic receivers. Our results demonstrate that they deliver complementary benefits: LO-free systems excel in proximity operations, while LO-dressed systems are eminently suitable for long-distance sensing at extremely low power levels. More specifically, LO-dressed systems achieve a significant signal-to-noise ratio (SNR) gain of approximately 44 dB over conventional RF receivers, exhibiting an effective coverage range extension over conventional RF receivers by a factor of 150. Furthermore, LO-dressed systems support higher-order quadrature amplitude modulation (QAM) at reduced symbol error rates (SER) compared to conventional RF receivers, hence significantly enhancing wireless communication performance.

New Paradigm for Unified Near-Field and Far-Field Wireless Communications

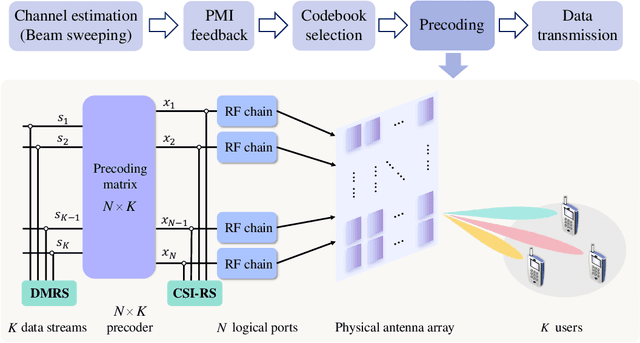
Current Type I and Type II codebooks in fifth generation (5G) wireless communications are limited in supporting the coexistence of far-field and near-field user equipments, as they are exclusively designed for far-field scenarios. To fill this knowledge gap and encourage relevant proposals by the 3rd Generation Partnership Project (3GPP), this article provides a novel codebook to facilitate a unified paradigm for the coexistence of far-field and near-field contexts. It ensures efficient precoding for all user equipments (UEs), while removing the need for the base station to identify whether one specific UE stays in either near-field or far-field regions. Additionally, our proposed codebook ensures compliance with current 3GPP standards for working flow and reference signals. Simulation results demonstrate the superior performance and versatility of our proposed codebook, validating its effectiveness in unifying near-field and far-field precoding for sixth-generation (6G) multiple-input multiple-output (MIMO) systems.

ScribbleVS: Scribble-Supervised Medical Image Segmentation via Dynamic Competitive Pseudo Label Selection

In clinical medicine, precise image segmentation can provide substantial support to clinicians. However, achieving such precision often requires a large amount of finely annotated data, which can be costly. Scribble annotation presents a more efficient alternative, boosting labeling efficiency. However, utilizing such minimal supervision for medical image segmentation training, especially with scribble annotations, poses significant challenges. To address these challenges, we introduce ScribbleVS, a novel framework that leverages scribble annotations. We introduce a Regional Pseudo Labels Diffusion Module to expand the scope of supervision and reduce the impact of noise present in pseudo labels. Additionally, we propose a Dynamic Competitive Selection module for enhanced refinement in selecting pseudo labels. Experiments conducted on the ACDC and MSCMRseg datasets have demonstrated promising results, achieving performance levels that even exceed those of fully supervised methodologies. The codes of this study are available at https://github.com/ortonwang/ScribbleVS.

Synergy-Guided Regional Supervision of Pseudo Labels for Semi-Supervised Medical Image Segmentation

Semi-supervised learning has received considerable attention for its potential to leverage abundant unlabeled data to enhance model robustness. Pseudo labeling is a widely used strategy in semi supervised learning. However, existing methods often suffer from noise contamination, which can undermine model performance. To tackle this challenge, we introduce a novel Synergy-Guided Regional Supervision of Pseudo Labels (SGRS-Net) framework. Built upon the mean teacher network, we employ a Mix Augmentation module to enhance the unlabeled data. By evaluating the synergy before and after augmentation, we strategically partition the pseudo labels into distinct regions. Additionally, we introduce a Region Loss Evaluation module to assess the loss across each delineated area. Extensive experiments conducted on the LA dataset have demonstrated superior performance over state-of-the-art techniques, underscoring the efficiency and practicality of our framework.

Wavenumber-Domain Near-Field Channel Estimation: Beyond the Fresnel Bound

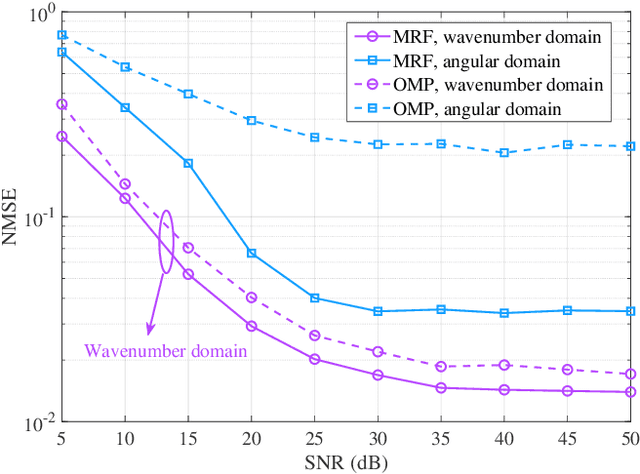
In the near-field context, the Fresnel approximation is typically employed to mathematically represent solvable functions of spherical waves. However, these efforts may fail to take into account the significant increase in the lower limit of the Fresnel approximation, known as the Fresnel distance. The lower bound of the Fresnel approximation imposes a constraint that becomes more pronounced as the array size grows. Beyond this constraint, the validity of the Fresnel approximation is broken. As a potential solution, the wavenumber-domain paradigm characterizes the spherical wave using a spectrum composed of a series of linear orthogonal bases. However, this approach falls short of covering the effects of the array geometry, especially when using Gaussian-mixed-model (GMM)-based von Mises-Fisher distributions to approximate all spectra. To fill this gap, this paper introduces a novel wavenumber-domain ellipse fitting (WDEF) method to tackle these challenges. Particularly, the channel is accurately estimated in the near-field region, by maximizing the closed-form likelihood function of the wavenumber-domain spectrum conditioned on the scatterers' geometric parameters. Simulation results are provided to demonstrate the robustness of the proposed scheme against both the distance and angles of arrival.

Unified Far-Field and Near-Field in Holographic MIMO: A Wavenumber-Domain Perspective

This article conceives a unified representation for near-field and far-field holographic multiple-input multiple-output (HMIMO) channels, addressing a practical design dilemma: "Why does the angular-domain representation no longer function effectively?" To answer this question, we pivot from the angular domain to the wavenumber domain and present a succinct overview of its underlying philosophy. In re-examining the Fourier plane-wave series expansion that recasts spherical propagation waves into a series of plane waves represented by Fourier harmonics, we characterize the HMIMO channel employing these Fourier harmonics having different wavenumbers. This approach, referred to as the wavenumebr-domain representation, facilitates a unified view across the far-field and the near-field. Furthermore, the limitations of the DFT basis are demonstrated when identifying the sparsity inherent to the HMIMO channel, motivating the development of a wavenumber-domain basis as an alternative. We then present some preliminary applications of the proposed wavenumber-domain basis in signal processing across both the far-field and near-field, along with several prospects for future HMIMO system designs based on the wavenumber domain.

Exploiting Structured Sparsity in Near Field: From the Perspective of Decomposition

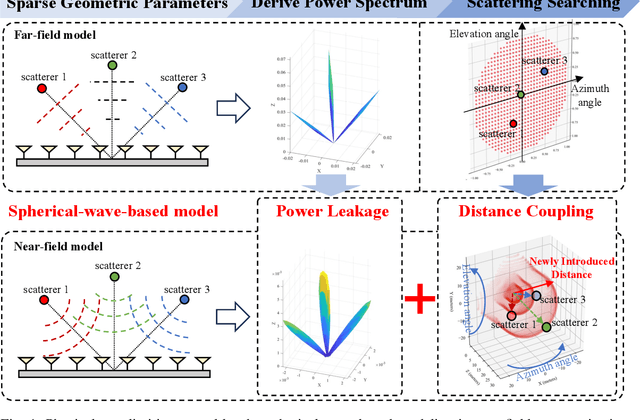
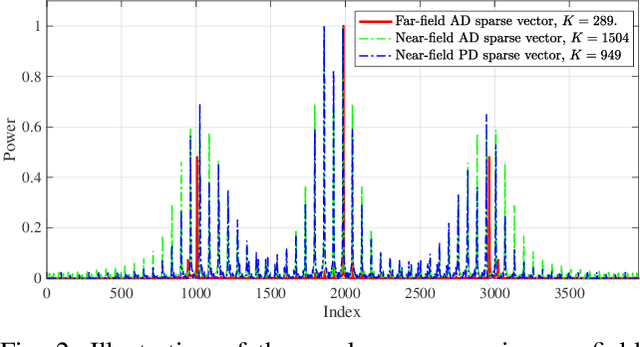
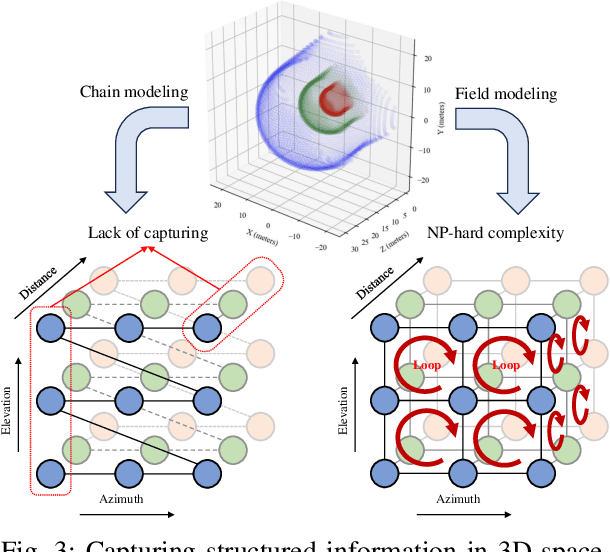
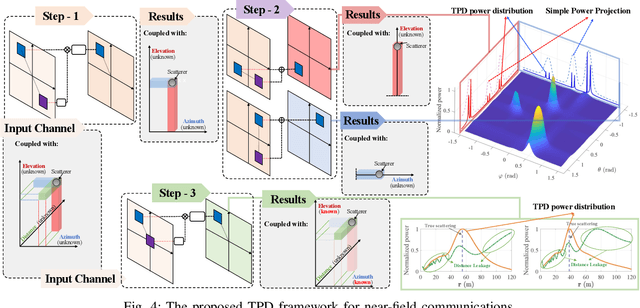
The structured sparsity can be leveraged in traditional far-field channels, greatly facilitating efficient sparse channel recovery by compressing the complexity of overheads to the level of the scatterer number. However, when experiencing a fundamental shift from planar-wave-based far-field modeling to spherical-wave-based near-field modeling, whether these benefits persist in the near-field regime remains an open issue. To answer this question, this article delves into structured sparsity in the near-field realm, examining its peculiarities and challenges. In particular, we present the key features of near-field structured sparsity in contrast to the far-field counterpart, drawing from both physical and mathematical perspectives. Upon unmasking the theoretical bottlenecks, we resort to bypassing them by decoupling the geometric parameters of the scatterers, termed the triple parametric decomposition (TPD) framework. It is demonstrated that our novel TPD framework can achieve robust recovery of near-field sparse channels by applying the potential structured sparsity and avoiding the curse of complexity and overhead.

Sparse Recovery for Holographic MIMO Channels: Leveraging the Clustered Sparsity

Envisioned as the next-generation transceiver technology, the holographic multiple-input-multiple-output (HMIMO) garners attention for its superior capabilities of fabricating electromagnetic (EM) waves. However, the densely packed antenna elements significantly increase the dimension of the HMIMO channel matrix, rendering traditional channel estimation methods inefficient. While the dimension curse can be relieved to avoid the proportional increase with the antenna density using the state-of-the-art wavenumber-domain sparse representation, the sparse recovery complexity remains tied to the order of non-zero elements in the sparse channel, which still considerably exceeds the number of scatterers. By modeling the inherent clustered sparsity using a Gaussian mixed model (GMM)-based von Mises-Fisher (vMF) distribution, the to-be-estimated channel characteristics can be compressed to the scatterer level. Upon the sparsity extraction, a novel wavenumber-domain expectation-maximization (WD-EM) algorithm is proposed to implement the cluster-by-cluster variational inference, thus significantly reducing the computational complexity. Simulation results verify the robustness of the proposed scheme across overheads and signal-to-noise ratio (SNR).

Holographic MIMO Systems, Their Channel Estimation and Performance

Holographic multiple-input multiple-output (MIMO) systems constitute a promising technology in support of next-generation wireless communications, thus paving the way for a smart programmable radio environment. However, despite its significant potential, further fundamental issues remain to be addressed, such as the acquisition of accurate channel information. Indeed, the conventional angular-domain channel representation is no longer adequate for characterizing the sparsity inherent in holographic MIMO channels. To fill this knowledge gap, in this article, we conceive a decomposition and reconstruction (DeRe)-based framework for facilitating the estimation of sparse channels in holographic MIMOs. In particular, the channel parameters involved in the steering vector, namely the azimuth and elevation angles plus the distance (AED), are decomposed for independently constructing their own covariance matrices. Then, the acquisition of each parameter can be formulated as a compressive sensing (CS) problem by harnessing the covariance matrix associated with each individual parameter. We demonstrate that our solution exhibits an improved performance and imposes a reduced pilot overhead, despite its reduced complexity. Finally, promising open research topics are highlighted to bridge the gap between the theory and the practical employment of holographic MIMO schemes.