Sparse Recovery for Holographic MIMO Channels: Leveraging the Clustered Sparsity

Envisioned as the next-generation transceiver technology, the holographic multiple-input-multiple-output (HMIMO) garners attention for its superior capabilities of fabricating electromagnetic (EM) waves. However, the densely packed antenna elements significantly increase the dimension of the HMIMO channel matrix, rendering traditional channel estimation methods inefficient. While the dimension curse can be relieved to avoid the proportional increase with the antenna density using the state-of-the-art wavenumber-domain sparse representation, the sparse recovery complexity remains tied to the order of non-zero elements in the sparse channel, which still considerably exceeds the number of scatterers. By modeling the inherent clustered sparsity using a Gaussian mixed model (GMM)-based von Mises-Fisher (vMF) distribution, the to-be-estimated channel characteristics can be compressed to the scatterer level. Upon the sparsity extraction, a novel wavenumber-domain expectation-maximization (WD-EM) algorithm is proposed to implement the cluster-by-cluster variational inference, thus significantly reducing the computational complexity. Simulation results verify the robustness of the proposed scheme across overheads and signal-to-noise ratio (SNR).

Channel Estimation for Holographic MIMO: Wavenumber-Domain Sparsity Inspired Approaches

This paper investigates the sparse channel estimation for holographic multiple-input multiple-output (HMIMO) systems. Given that the wavenumber-domain representation is based on a series of Fourier harmonics that are in essence a series of orthogonal basis functions, a novel wavenumber-domain sparsifying basis is designed to expose the sparsity inherent in HMIMO channels. Furthermore, by harnessing the beneficial sparsity in the wavenumber domain, the sparse estimation of HMIMO channels is structured as a compressed sensing problem, which can be efficiently solved by our proposed wavenumber-domain orthogonal matching pursuit (WD-OMP) algorithm. Finally, numerical results demonstrate that the proposed wavenumber-domain sparsifying basis maintains its detection accuracy regardless of the number of antenna elements and antenna spacing. Additionally, in the case of antenna spacing being much less than half a wavelength, the wavenumber-domain approach remains highly accurate in identifying the significant angular power of HMIMO channels.

M-Walk: Learning to Walk over Graphs using Monte Carlo Tree Search

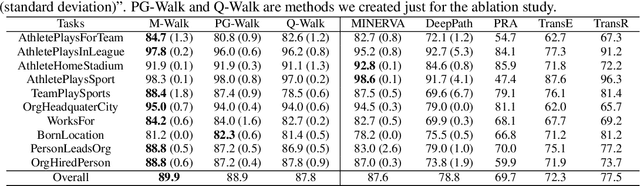
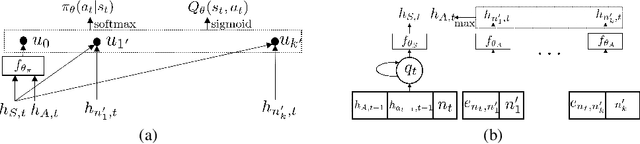
Learning to walk over a graph towards a target node for a given query and a source node is an important problem in applications such as knowledge base completion (KBC). It can be formulated as a reinforcement learning (RL) problem with a known state transition model. To overcome the challenge of sparse rewards, we develop a graph-walking agent called M-Walk, which consists of a deep recurrent neural network (RNN) and Monte Carlo Tree Search (MCTS). The RNN encodes the state (i.e., history of the walked path) and maps it separately to a policy and Q-values. In order to effectively train the agent from sparse rewards, we combine MCTS with the neural policy to generate trajectories yielding more positive rewards. From these trajectories, the network is improved in an off-policy manner using Q-learning, which modifies the RNN policy via parameter sharing. Our proposed RL algorithm repeatedly applies this policy-improvement step to learn the model. At test time, MCTS is combined with the neural policy to predict the target node. Experimental results on several graph-walking benchmarks show that M-Walk is able to learn better policies than other RL-based methods, which are mainly based on policy gradients. M-Walk also outperforms traditional KBC baselines.