Harnessing Rydberg Atomic Receivers: From Quantum Physics to Wireless Communications

The intrinsic integration of Rydberg atomic receivers into wireless communication systems is proposed, by harnessing the principles of quantum physics in wireless communications. More particularly, we conceive a pair of Rydberg atomic receivers, one incorporates a local oscillator (LO), referred to as an LO-dressed receiver, while the other operates without an LO and is termed an LO-free receiver. The appropriate wireless model is developed for each configuration, elaborating on the receiver's responses to the radio frequency (RF) signal, on the potential noise sources, and on the system performance. Next, we investigate the association distortion effects that might occur, specifically demonstrating the boundaries of linear dynamic regions, which provides critical insights into its practical implementations in wireless systems. Extensive simulation results are provided for characterizing the performance of wireless systems, harnessing this pair of Rydberg atomic receivers. Our results demonstrate that they deliver complementary benefits: LO-free systems excel in proximity operations, while LO-dressed systems are eminently suitable for long-distance sensing at extremely low power levels. More specifically, LO-dressed systems achieve a significant signal-to-noise ratio (SNR) gain of approximately 44 dB over conventional RF receivers, exhibiting an effective coverage range extension over conventional RF receivers by a factor of 150. Furthermore, LO-dressed systems support higher-order quadrature amplitude modulation (QAM) at reduced symbol error rates (SER) compared to conventional RF receivers, hence significantly enhancing wireless communication performance.

Wavenumber-Domain Near-Field Channel Estimation: Beyond the Fresnel Bound

In the near-field context, the Fresnel approximation is typically employed to mathematically represent solvable functions of spherical waves. However, these efforts may fail to take into account the significant increase in the lower limit of the Fresnel approximation, known as the Fresnel distance. The lower bound of the Fresnel approximation imposes a constraint that becomes more pronounced as the array size grows. Beyond this constraint, the validity of the Fresnel approximation is broken. As a potential solution, the wavenumber-domain paradigm characterizes the spherical wave using a spectrum composed of a series of linear orthogonal bases. However, this approach falls short of covering the effects of the array geometry, especially when using Gaussian-mixed-model (GMM)-based von Mises-Fisher distributions to approximate all spectra. To fill this gap, this paper introduces a novel wavenumber-domain ellipse fitting (WDEF) method to tackle these challenges. Particularly, the channel is accurately estimated in the near-field region, by maximizing the closed-form likelihood function of the wavenumber-domain spectrum conditioned on the scatterers' geometric parameters. Simulation results are provided to demonstrate the robustness of the proposed scheme against both the distance and angles of arrival.

Unified Far-Field and Near-Field in Holographic MIMO: A Wavenumber-Domain Perspective

This article conceives a unified representation for near-field and far-field holographic multiple-input multiple-output (HMIMO) channels, addressing a practical design dilemma: "Why does the angular-domain representation no longer function effectively?" To answer this question, we pivot from the angular domain to the wavenumber domain and present a succinct overview of its underlying philosophy. In re-examining the Fourier plane-wave series expansion that recasts spherical propagation waves into a series of plane waves represented by Fourier harmonics, we characterize the HMIMO channel employing these Fourier harmonics having different wavenumbers. This approach, referred to as the wavenumebr-domain representation, facilitates a unified view across the far-field and the near-field. Furthermore, the limitations of the DFT basis are demonstrated when identifying the sparsity inherent to the HMIMO channel, motivating the development of a wavenumber-domain basis as an alternative. We then present some preliminary applications of the proposed wavenumber-domain basis in signal processing across both the far-field and near-field, along with several prospects for future HMIMO system designs based on the wavenumber domain.

Exploiting Structured Sparsity in Near Field: From the Perspective of Decomposition

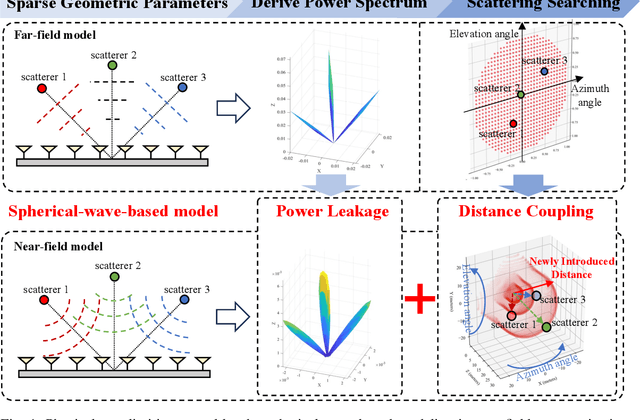
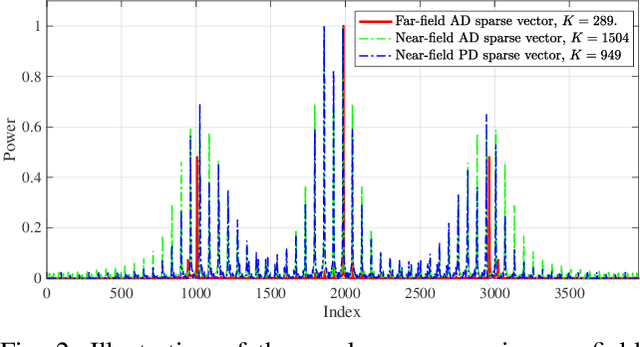
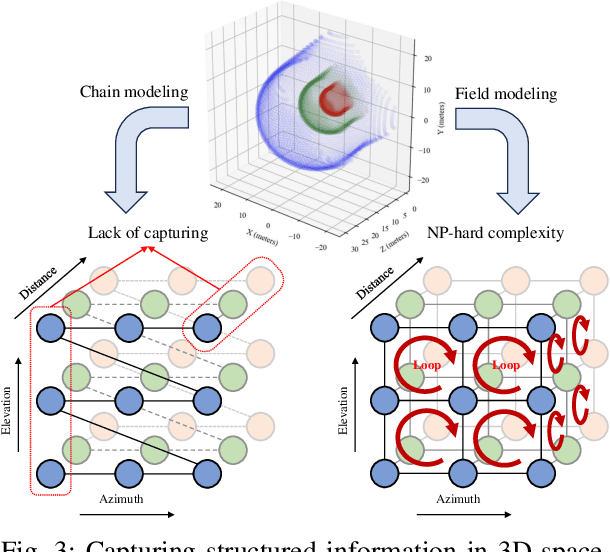
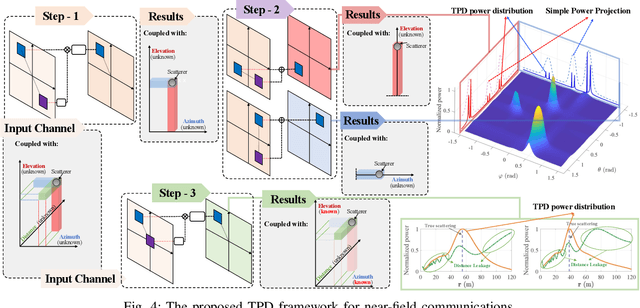
The structured sparsity can be leveraged in traditional far-field channels, greatly facilitating efficient sparse channel recovery by compressing the complexity of overheads to the level of the scatterer number. However, when experiencing a fundamental shift from planar-wave-based far-field modeling to spherical-wave-based near-field modeling, whether these benefits persist in the near-field regime remains an open issue. To answer this question, this article delves into structured sparsity in the near-field realm, examining its peculiarities and challenges. In particular, we present the key features of near-field structured sparsity in contrast to the far-field counterpart, drawing from both physical and mathematical perspectives. Upon unmasking the theoretical bottlenecks, we resort to bypassing them by decoupling the geometric parameters of the scatterers, termed the triple parametric decomposition (TPD) framework. It is demonstrated that our novel TPD framework can achieve robust recovery of near-field sparse channels by applying the potential structured sparsity and avoiding the curse of complexity and overhead.

Sparse Recovery for Holographic MIMO Channels: Leveraging the Clustered Sparsity

Envisioned as the next-generation transceiver technology, the holographic multiple-input-multiple-output (HMIMO) garners attention for its superior capabilities of fabricating electromagnetic (EM) waves. However, the densely packed antenna elements significantly increase the dimension of the HMIMO channel matrix, rendering traditional channel estimation methods inefficient. While the dimension curse can be relieved to avoid the proportional increase with the antenna density using the state-of-the-art wavenumber-domain sparse representation, the sparse recovery complexity remains tied to the order of non-zero elements in the sparse channel, which still considerably exceeds the number of scatterers. By modeling the inherent clustered sparsity using a Gaussian mixed model (GMM)-based von Mises-Fisher (vMF) distribution, the to-be-estimated channel characteristics can be compressed to the scatterer level. Upon the sparsity extraction, a novel wavenumber-domain expectation-maximization (WD-EM) algorithm is proposed to implement the cluster-by-cluster variational inference, thus significantly reducing the computational complexity. Simulation results verify the robustness of the proposed scheme across overheads and signal-to-noise ratio (SNR).

Wavenumber Domain Sparse Channel Estimation in Holographic MIMO

In this paper, we investigate the sparse channel estimation in holographic multiple-input multiple-output (HMIMO) systems. The conventional angular-domain representation fails to capture the continuous angular power spectrum characterized by the spatially-stationary electromagnetic random field, thus leading to the ambiguous detection of the significant angular power, which is referred to as the power leakage. To tackle this challenge, the HMIMO channel is represented in the wavenumber domain for exploring its cluster-dominated sparsity. Specifically, a finite set of Fourier harmonics acts as a series of sampling probes to encapsulate the integral of the power spectrum over specific angular regions. This technique effectively eliminates power leakage resulting from power mismatches induced by the use of discrete angular-domain probes. Next, the channel estimation problem is recast as a sparse recovery of the significant angular power spectrum over the continuous integration region. We then propose an accompanying graph-cut-based swap expansion (GCSE) algorithm to extract beneficial sparsity inherent in HMIMO channels. Numerical results demonstrate that this wavenumber-domainbased GCSE approach achieves robust performance with rapid convergence.

Location Tracking for Reconfigurable Intelligent Surfaces Aided Vehicle Platoons: Diverse Sparsities Inspired Approaches

In this paper, we investigate the employment of reconfigurable intelligent surfaces (RISs) into vehicle platoons, functioning in tandem with a base station (BS) in support of the high-precision location tracking. In particular, the use of a RIS imposes additional structured sparsity that, when paired with the initial sparse line-of-sight (LoS) channels of the BS, facilitates beneficial group sparsity. The resultant group sparsity significantly enriches the energies of the original direct-only channel, enabling a greater concentration of the LoS channel energies emanated from the same vehicle location index. Furthermore, the burst sparsity is exposed by representing the non-line-of-sight (NLoS) channels as their sparse copies. This thus constitutes the philosophy of the diverse sparsities of interest. Then, a diverse dynamic layered structured sparsity (DiLuS) framework is customized for capturing different priors for this pair of sparsities, based upon which the location tracking problem is formulated as a maximum a posterior (MAP) estimate of the location. Nevertheless, the tracking issue is highly intractable due to the ill-conditioned sensing matrix, intricately coupled latent variables associated with the BS and RIS, and the spatialtemporal correlations among the vehicle platoon. To circumvent these hurdles, we propose an efficient algorithm, namely DiLuS enabled spatial-temporal platoon localization (DiLuS-STPL), which incorporates both variational Bayesian inference (VBI) and message passing techniques for recursively achieving parameter updates in a turbo-like way. Finally, we demonstrate through extensive simulation results that the localization relying exclusively upon a BS and a RIS may achieve the comparable precision performance obtained by the two individual BSs, along with the robustness and superiority of our proposed algorithm as compared to various benchmark schemes.