Yi Tian
CellMamba: Adaptive Mamba for Accurate and Efficient Cell Detection
Dec 25, 2025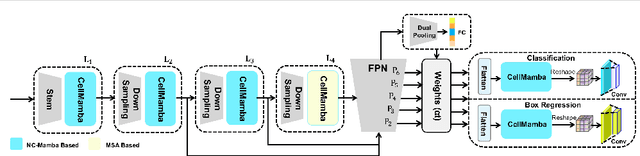
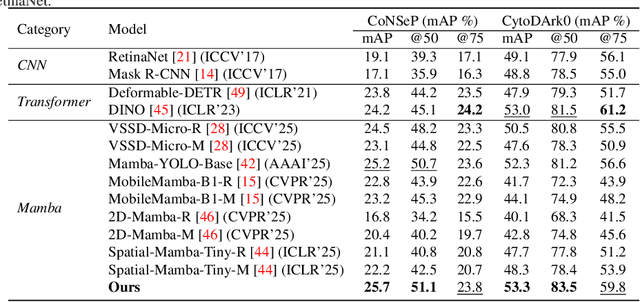
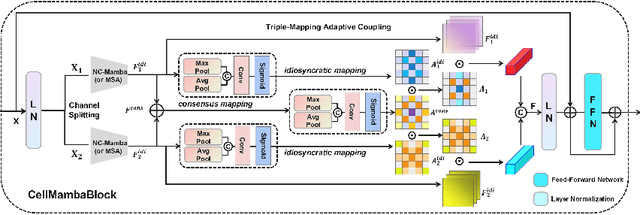
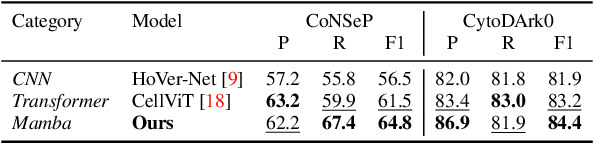
Abstract:Cell detection in pathological images presents unique challenges due to densely packed objects, subtle inter-class differences, and severe background clutter. In this paper, we propose CellMamba, a lightweight and accurate one-stage detector tailored for fine-grained biomedical instance detection. Built upon a VSSD backbone, CellMamba integrates CellMamba Blocks, which couple either NC-Mamba or Multi-Head Self-Attention (MSA) with a novel Triple-Mapping Adaptive Coupling (TMAC) module. TMAC enhances spatial discriminability by splitting channels into two parallel branches, equipped with dual idiosyncratic and one consensus attention map, adaptively fused to preserve local sensitivity and global consistency. Furthermore, we design an Adaptive Mamba Head that fuses multi-scale features via learnable weights for robust detection under varying object sizes. Extensive experiments on two public datasets-CoNSeP and CytoDArk0-demonstrate that CellMamba outperforms both CNN-based, Transformer-based, and Mamba-based baselines in accuracy, while significantly reducing model size and inference latency. Our results validate CellMamba as an efficient and effective solution for high-resolution cell detection.
Advancing Cross-Organ Domain Generalization with Test-Time Style Transfer and Diversity Enhancement
Mar 24, 2025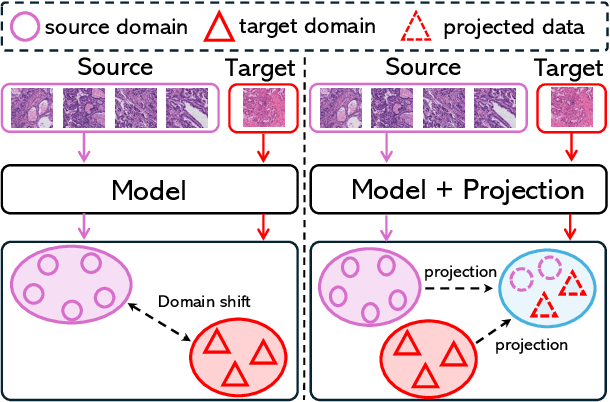



Abstract:Deep learning has made significant progress in addressing challenges in various fields including computational pathology (CPath). However, due to the complexity of the domain shift problem, the performance of existing models will degrade, especially when it comes to multi-domain or cross-domain tasks. In this paper, we propose a Test-time style transfer (T3s) that uses a bidirectional mapping mechanism to project the features of the source and target domains into a unified feature space, enhancing the generalization ability of the model. To further increase the style expression space, we introduce a Cross-domain style diversification module (CSDM) to ensure the orthogonality between style bases. In addition, data augmentation and low-rank adaptation techniques are used to improve feature alignment and sensitivity, enabling the model to adapt to multi-domain inputs effectively. Our method has demonstrated effectiveness on three unseen datasets.
CLIP-driven Dual Feature Enhancing Network for Gaze Estimation
Feb 27, 2025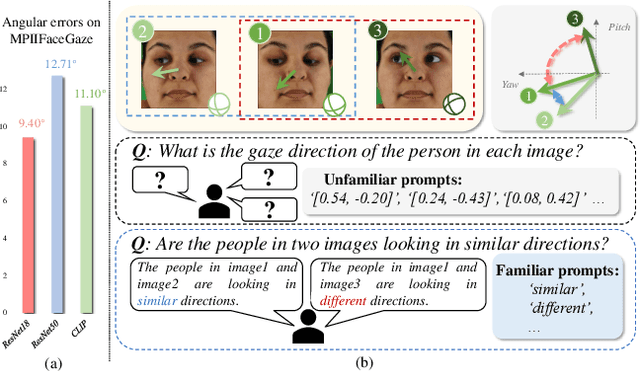
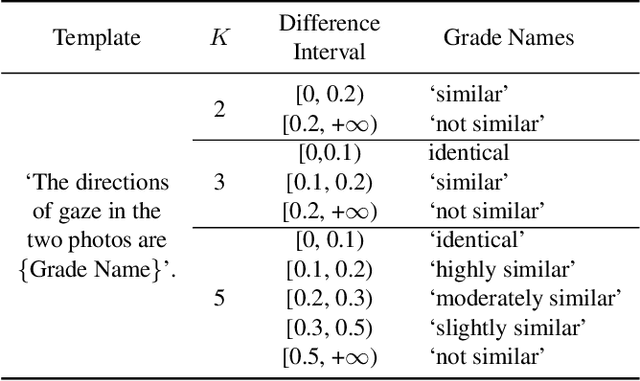
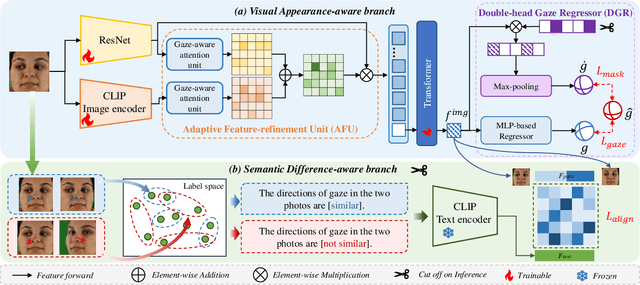
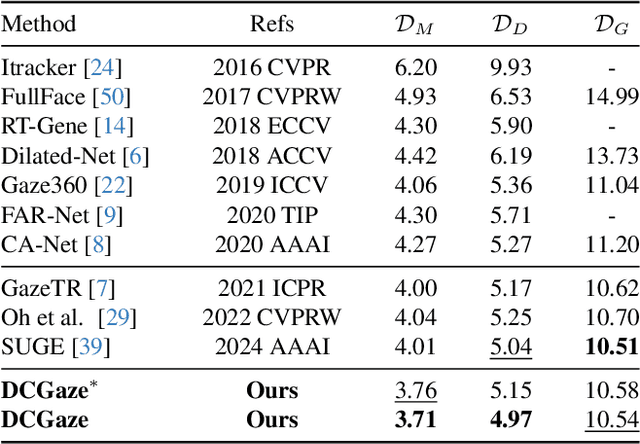
Abstract:The complex application scenarios have raised critical requirements for precise and generalizable gaze estimation methods. Recently, the pre-trained CLIP has achieved remarkable performance on various vision tasks, but its potentials have not been fully exploited in gaze estimation. In this paper, we propose a novel CLIP-driven Dual Feature Enhancing Network (CLIP-DFENet), which boosts gaze estimation performance with the help of CLIP under a novel `main-side' collaborative enhancing strategy. Accordingly, a Language-driven Differential Module (LDM) is designed on the basis of the CLIP's text encoder to reveal the semantic difference of gaze. This module could empower our Core Feature Extractor with the capability of characterizing the gaze-related semantic information. Moreover, a Vision-driven Fusion Module (VFM) is introduced to strengthen the generalized and valuable components of visual embeddings obtained via CLIP's image encoder, and utilizes them to further improve the generalization of the features captured by Core Feature Extractor. Finally, a robust Double-head Gaze Regressor is adopted to map the enhanced features to gaze directions. Extensive experimental results on four challenging datasets over within-domain and cross-domain tasks demonstrate the discriminability and generalizability of our CLIP-DFENet.
SDformerFlow: Spatiotemporal swin spikeformer for event-based optical flow estimation
Sep 06, 2024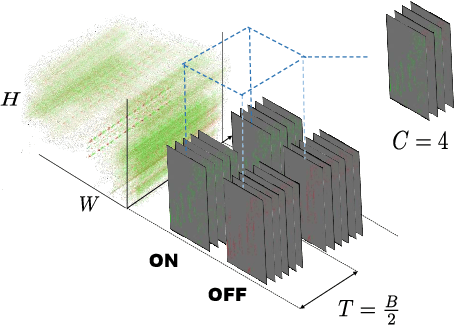
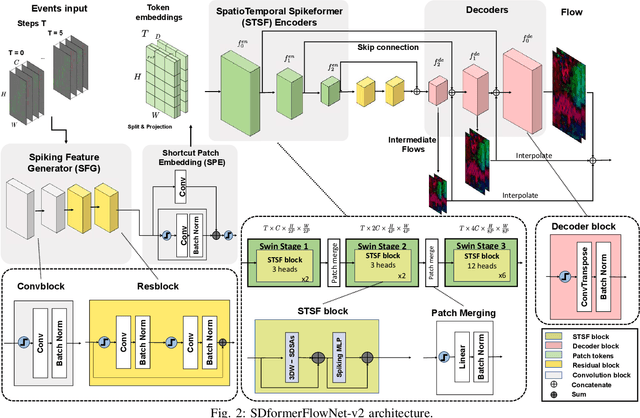
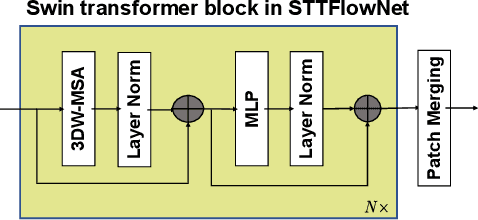
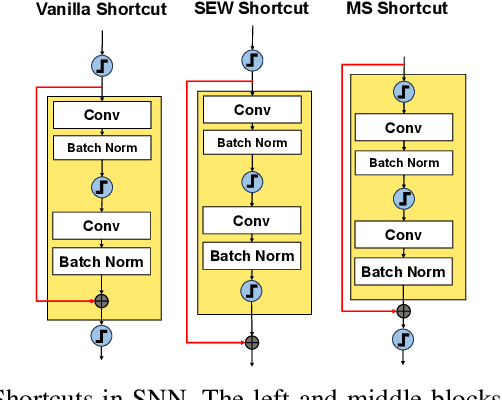
Abstract:Event cameras generate asynchronous and sparse event streams capturing changes in light intensity. They offer significant advantages over conventional frame-based cameras, such as a higher dynamic range and an extremely faster data rate, making them particularly useful in scenarios involving fast motion or challenging lighting conditions. Spiking neural networks (SNNs) share similar asynchronous and sparse characteristics and are well-suited for processing data from event cameras. Inspired by the potential of transformers and spike-driven transformers (spikeformers) in other computer vision tasks, we propose two solutions for fast and robust optical flow estimation for event cameras: STTFlowNet and SDformerFlow. STTFlowNet adopts a U-shaped artificial neural network (ANN) architecture with spatiotemporal shifted window self-attention (swin) transformer encoders, while SDformerFlow presents its fully spiking counterpart, incorporating swin spikeformer encoders. Furthermore, we present two variants of the spiking version with different neuron models. Our work is the first to make use of spikeformers for dense optical flow estimation. We conduct end-to-end training for all models using supervised learning. Our results yield state-of-the-art performance among SNN-based event optical flow methods on both the DSEC and MVSEC datasets, and show significant reduction in power consumption compared to the equivalent ANNs.
Convex and Non-Convex Optimization under Generalized Smoothness
Jun 02, 2023
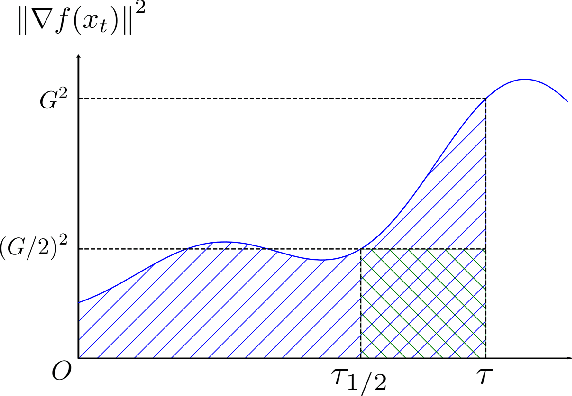

Abstract:Classical analysis of convex and non-convex optimization methods often requires the Lipshitzness of the gradient, which limits the analysis to functions bounded by quadratics. Recent work relaxed this requirement to a non-uniform smoothness condition with the Hessian norm bounded by an affine function of the gradient norm, and proved convergence in the non-convex setting via gradient clipping, assuming bounded noise. In this paper, we further generalize this non-uniform smoothness condition and develop a simple, yet powerful analysis technique that bounds the gradients along the trajectory, thereby leading to stronger results for both convex and non-convex optimization problems. In particular, we obtain the classical convergence rates for (stochastic) gradient descent and Nesterov's accelerated gradient method in the convex and/or non-convex setting under this general smoothness condition. The new analysis approach does not require gradient clipping and allows heavy-tailed noise with bounded variance in the stochastic setting.
PhysBench: A Benchmark Framework for Remote Physiological Sensing with New Dataset and Baseline
May 07, 2023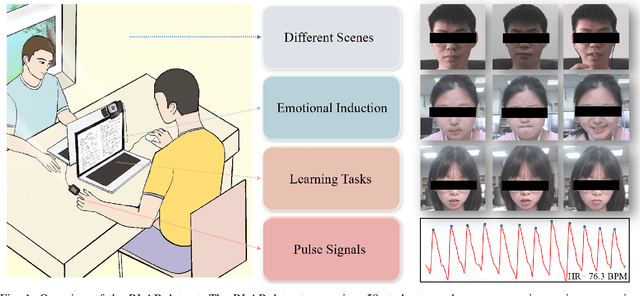
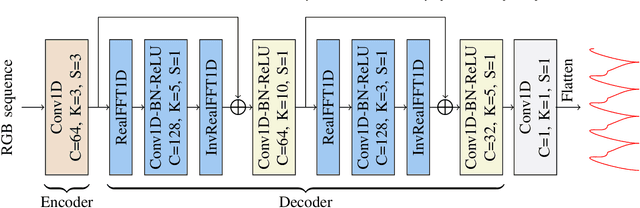
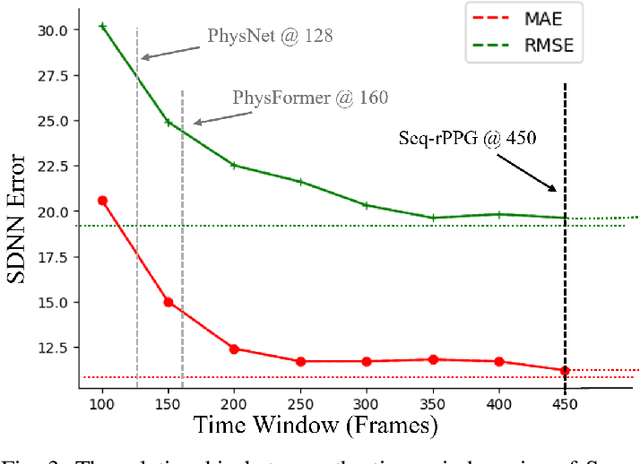
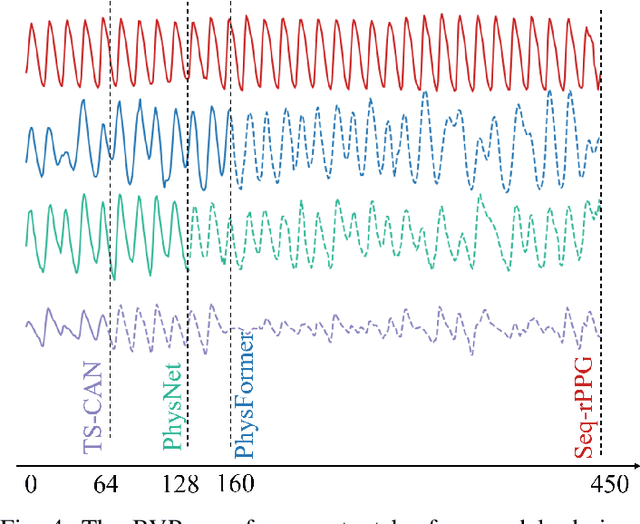
Abstract:In recent years, due to the widespread use of internet videos, physiological remote sensing has gained more and more attention in the fields of affective computing and telemedicine. Recovering physiological signals from facial videos is a challenging task that involves a series of preprocessing, image algorithms, and post-processing to finally restore waveforms. We propose a complete and efficient end-to-end training and testing framework that provides fair comparisons for different algorithms through unified preprocessing and post-processing. In addition, we introduce a highly synchronized lossless format dataset along with a lightweight algorithm. The dataset contains over 32 hours (3.53M frames) of video from 58 subjects; by training on our collected dataset both our proposed algorithm as well as existing ones can achieve improvements.
Can Direct Latent Model Learning Solve Linear Quadratic Gaussian Control?
Dec 30, 2022Abstract:We study the task of learning state representations from potentially high-dimensional observations, with the goal of controlling an unknown partially observable system. We pursue a direct latent model learning approach, where a dynamic model in some latent state space is learned by predicting quantities directly related to planning (e.g., costs) without reconstructing the observations. In particular, we focus on an intuitive cost-driven state representation learning method for solving Linear Quadratic Gaussian (LQG) control, one of the most fundamental partially observable control problems. As our main results, we establish finite-sample guarantees of finding a near-optimal state representation function and a near-optimal controller using the directly learned latent model. To the best of our knowledge, despite various empirical successes, prior to this work it was unclear if such a cost-driven latent model learner enjoys finite-sample guarantees. Our work underscores the value of predicting multi-step costs, an idea that is key to our theory, and notably also an idea that is known to be empirically valuable for learning state representations.
Byzantine-Robust Federated Linear Bandits
Apr 03, 2022Abstract:In this paper, we study a linear bandit optimization problem in a federated setting where a large collection of distributed agents collaboratively learn a common linear bandit model. Standard federated learning algorithms applied to this setting are vulnerable to Byzantine attacks on even a small fraction of agents. We propose a novel algorithm with a robust aggregation oracle that utilizes the geometric median. We prove that our proposed algorithm is robust to Byzantine attacks on fewer than half of agents and achieves a sublinear $\tilde{\mathcal{O}}({T^{3/4}})$ regret with $\mathcal{O}(\sqrt{T})$ steps of communication in $T$ steps. Moreover, we make our algorithm differentially private via a tree-based mechanism. Finally, if the level of corruption is known to be small, we show that using the geometric median of mean oracle for robust aggregation further improves the regret bound.
Complexity Lower Bounds for Nonconvex-Strongly-Concave Min-Max Optimization
Apr 18, 2021
Abstract:We provide a first-order oracle complexity lower bound for finding stationary points of min-max optimization problems where the objective function is smooth, nonconvex in the minimization variable, and strongly concave in the maximization variable. We establish a lower bound of $\Omega\left(\sqrt{\kappa}\epsilon^{-2}\right)$ for deterministic oracles, where $\epsilon$ defines the level of approximate stationarity and $\kappa$ is the condition number. Our analysis shows that the upper bound achieved in (Lin et al., 2020b) is optimal in the $\epsilon$ and $\kappa$ dependence up to logarithmic factors. For stochastic oracles, we provide a lower bound of $\Omega\left(\sqrt{\kappa}\epsilon^{-2} + \kappa^{1/3}\epsilon^{-4}\right)$. It suggests that there is a significant gap between the upper bound $\mathcal{O}(\kappa^3 \epsilon^{-4})$ in (Lin et al., 2020a) and our lower bound in the condition number dependence.
Provably Efficient Algorithms for Multi-Objective Competitive RL
Feb 05, 2021
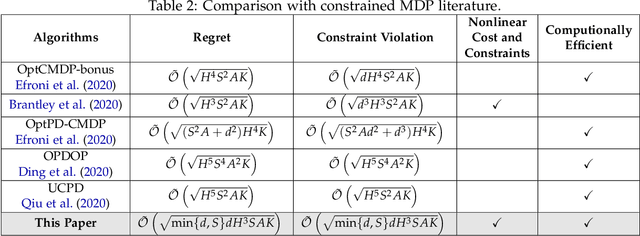
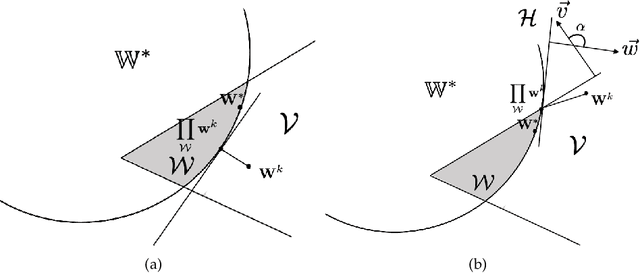
Abstract:We study multi-objective reinforcement learning (RL) where an agent's reward is represented as a vector. In settings where an agent competes against opponents, its performance is measured by the distance of its average return vector to a target set. We develop statistically and computationally efficient algorithms to approach the associated target set. Our results extend Blackwell's approachability theorem (Blackwell, 1956) to tabular RL, where strategic exploration becomes essential. The algorithms presented are adaptive; their guarantees hold even without Blackwell's approachability condition. If the opponents use fixed policies, we give an improved rate of approaching the target set while also tackling the more ambitious goal of simultaneously minimizing a scalar cost function. We discuss our analysis for this special case by relating our results to previous works on constrained RL. To our knowledge, this work provides the first provably efficient algorithms for vector-valued Markov games and our theoretical guarantees are near-optimal.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge