Provably Efficient Online Agnostic Learning in Markov Games

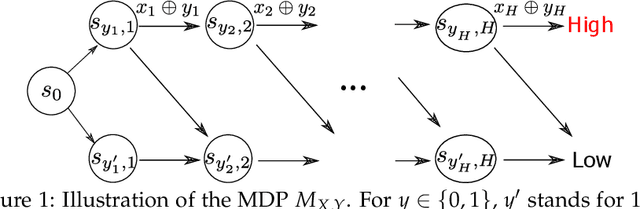
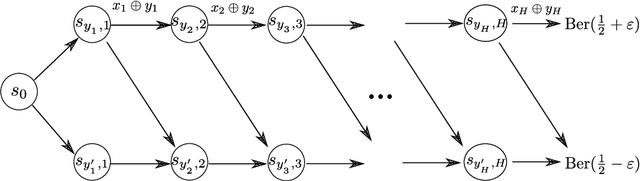
We study online agnostic learning, a problem that arises in episodic multi-agent reinforcement learning where the actions of the opponents are unobservable. We show that in this challenging setting, achieving sublinear regret against the best response in hindsight is statistically hard. We then consider a weaker notion of regret, and present an algorithm that achieves after $K$ episodes a sublinear $\tilde{\mathcal{O}}(K^{3/4})$ regret. This is the first sublinear regret bound (to our knowledge) in the online agnostic setting. Importantly, our regret bound is independent of the size of the opponents' action spaces. As a result, even when the opponents' actions are fully observable, our regret bound improves upon existing analysis (e.g., (Xie et al., 2020)) by an exponential factor in the number of opponents.