Yanze Wang
ExplainableGuard: Interpretable Adversarial Defense for Large Language Models Using Chain-of-Thought Reasoning
Nov 15, 2025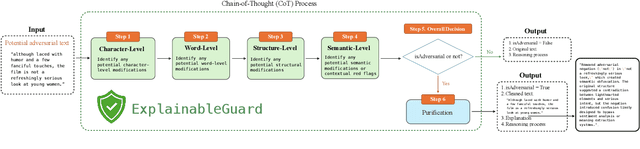
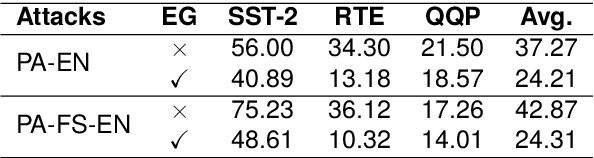
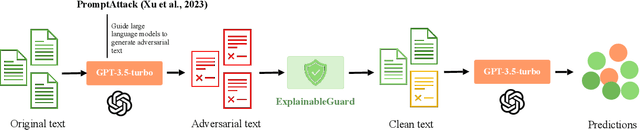
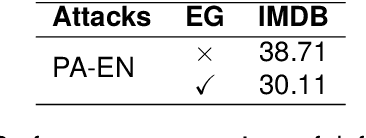
Abstract:Large Language Models (LLMs) are increasingly vulnerable to adversarial attacks that can subtly manipulate their outputs. While various defense mechanisms have been proposed, many operate as black boxes, lacking transparency in their decision-making. This paper introduces ExplainableGuard, an interpretable adversarial defense framework leveraging the chain-of-thought (CoT) reasoning capabilities of DeepSeek-Reasoner. Our approach not only detects and neutralizes adversarial perturbations in text but also provides step-by-step explanations for each defense action. We demonstrate how tailored CoT prompts guide the LLM to perform a multi-faceted analysis (character, word, structural, and semantic) and generate a purified output along with a human-readable justification. Preliminary results on the GLUE Benchmark and IMDB Movie Reviews dataset show promising defense efficacy. Additionally, a human evaluation study reveals that ExplainableGuard's explanations outperform ablated variants in clarity, specificity, and actionability, with a 72.5% deployability-trust rating, underscoring its potential for more trustworthy LLM deployments.
Should I Trust You? Detecting Deception in Negotiations using Counterfactual RL
Feb 18, 2025Abstract:An increasingly prevalent socio-technical problem is people being taken in by offers that sound ``too good to be true'', where persuasion and trust shape decision-making. This paper investigates how \abr{ai} can help detect these deceptive scenarios. We analyze how humans strategically deceive each other in \textit{Diplomacy}, a board game that requires both natural language communication and strategic reasoning. This requires extracting logical forms of proposed agreements in player communications and computing the relative rewards of the proposal using agents' value functions. Combined with text-based features, this can improve our deception detection. Our method detects human deception with a high precision when compared to a Large Language Model approach that flags many true messages as deceptive. Future human-\abr{ai} interaction tools can build on our methods for deception detection by triggering \textit{friction} to give users a chance of interrogating suspicious proposals.
Generalized Flow Matching for Transition Dynamics Modeling
Oct 19, 2024



Abstract:Simulating transition dynamics between metastable states is a fundamental challenge in dynamical systems and stochastic processes with wide real-world applications in understanding protein folding, chemical reactions and neural activities. However, the computational challenge often lies on sampling exponentially many paths in which only a small fraction ends in the target metastable state due to existence of high energy barriers. To amortize the cost, we propose a data-driven approach to warm-up the simulation by learning nonlinear interpolations from local dynamics. Specifically, we infer a potential energy function from local dynamics data. To find plausible paths between two metastable states, we formulate a generalized flow matching framework that learns a vector field to sample propable paths between the two marginal densities under the learned energy function. Furthermore, we iteratively refine the model by assigning importance weights to the sampled paths and buffering more likely paths for training. We validate the effectiveness of the proposed method to sample probable paths on both synthetic and real-world molecular systems.
More Victories, Less Cooperation: Assessing Cicero's Diplomacy Play
Jun 07, 2024Abstract:The boardgame Diplomacy is a challenging setting for communicative and cooperative artificial intelligence. The most prominent communicative Diplomacy AI, Cicero, has excellent strategic abilities, exceeding human players. However, the best Diplomacy players master communication, not just tactics, which is why the game has received attention as an AI challenge. This work seeks to understand the degree to which Cicero succeeds at communication. First, we annotate in-game communication with abstract meaning representation to separate in-game tactics from general language. Second, we run two dozen games with humans and Cicero, totaling over 200 human-player hours of competition. While AI can consistently outplay human players, AI-Human communication is still limited because of AI's difficulty with deception and persuasion. This shows that Cicero relies on strategy and has not yet reached the full promise of communicative and cooperative AI.
Reinforcement Learning With Reward Machines in Stochastic Games
May 27, 2023Abstract:We investigate multi-agent reinforcement learning for stochastic games with complex tasks, where the reward functions are non-Markovian. We utilize reward machines to incorporate high-level knowledge of complex tasks. We develop an algorithm called Q-learning with reward machines for stochastic games (QRM-SG), to learn the best-response strategy at Nash equilibrium for each agent. In QRM-SG, we define the Q-function at a Nash equilibrium in augmented state space. The augmented state space integrates the state of the stochastic game and the state of reward machines. Each agent learns the Q-functions of all agents in the system. We prove that Q-functions learned in QRM-SG converge to the Q-functions at a Nash equilibrium if the stage game at each time step during learning has a global optimum point or a saddle point, and the agents update Q-functions based on the best-response strategy at this point. We use the Lemke-Howson method to derive the best-response strategy given current Q-functions. The three case studies show that QRM-SG can learn the best-response strategies effectively. QRM-SG learns the best-response strategies after around 7500 episodes in Case Study I, 1000 episodes in Case Study II, and 1500 episodes in Case Study III, while baseline methods such as Nash Q-learning and MADDPG fail to converge to the Nash equilibrium in all three case studies.
Learning Sparse and Continuous Graph Structures for Multivariate Time Series Forecasting
Jan 24, 2022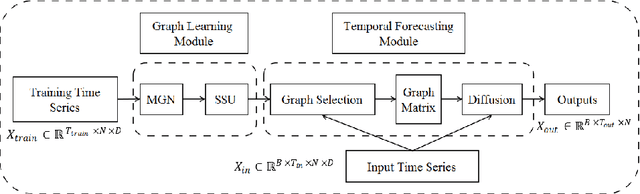

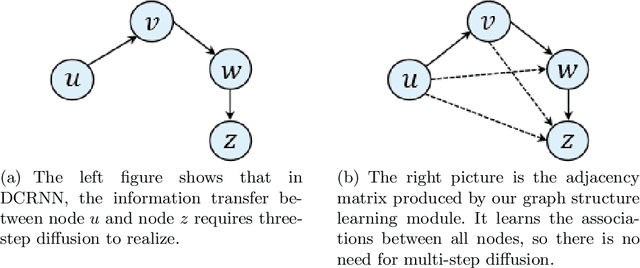
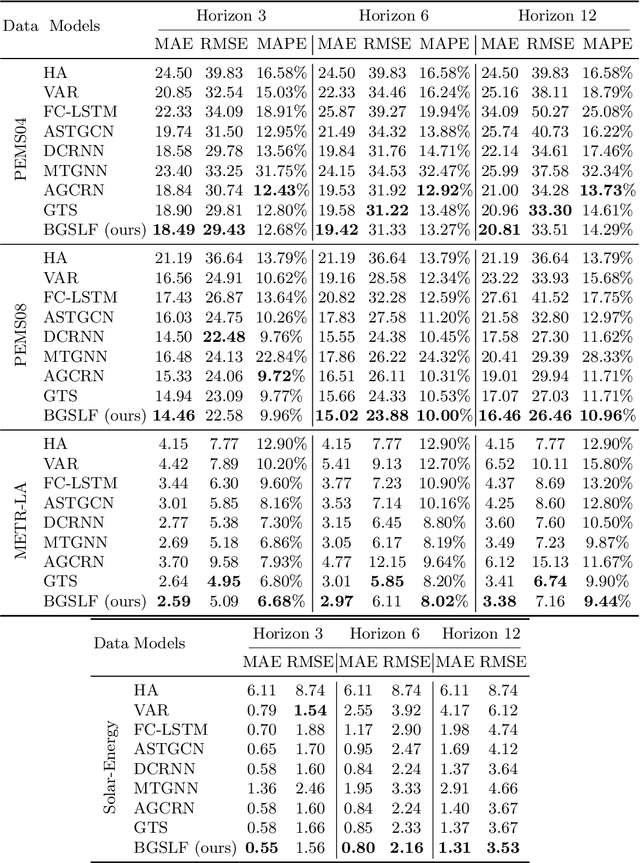
Abstract:Accurate forecasting of multivariate time series is an extensively studied subject in finance, transportation, and computer science. Fully mining the correlation and causation between the variables in a multivariate time series exhibits noticeable results in improving the performance of a time series model. Recently, some models have explored the dependencies between variables through end-to-end graph structure learning without the need for pre-defined graphs. However, most current models do not incorporate the trade-off between effectiveness and flexibility and lack the guidance of domain knowledge in the design of graph learning algorithms. Besides, they have issues generating sparse graph structures, which pose challenges to end-to-end learning. In this paper, we propose Learning Sparse and Continuous Graphs for Forecasting (LSCGF), a novel deep learning model that joins graph learning and forecasting. Technically, LSCGF leverages the spatial information into convolutional operation and extracts temporal dynamics using the diffusion convolution recurrent network. At the same time, we propose a brand new method named Smooth Sparse Unit (SSU) to learn sparse and continuous graph adjacency matrix. Extensive experiments on three real-world datasets demonstrate that our model achieves state-of-the-art performances with minor trainable parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge