Specification-Driven Video Search via Foundation Models and Formal Verification

The increasing abundance of video data enables users to search for events of interest, e.g., emergency incidents. Meanwhile, it raises new concerns, such as the need for preserving privacy. Existing approaches to video search require either manual inspection or a deep learning model with massive training. We develop a method that uses recent advances in vision and language models, as well as formal methods, to search for events of interest in video clips automatically and efficiently. The method consists of an algorithm to map text-based event descriptions into linear temporal logic over finite traces (LTL$_f$) and an algorithm to construct an automaton encoding the video information. Then, the method formally verifies the automaton representing the video against the LTL$_f$ specifications and adds the pertinent video clips to the search result if the automaton satisfies the specifications. We provide qualitative and quantitative analysis to demonstrate the video-searching capability of the proposed method. It achieves over 90 percent precision in searching over privacy-sensitive videos and a state-of-the-art autonomous driving dataset.

Reinforcement Learning with Temporal-Logic-Based Causal Diagrams

We study a class of reinforcement learning (RL) tasks where the objective of the agent is to accomplish temporally extended goals. In this setting, a common approach is to represent the tasks as deterministic finite automata (DFA) and integrate them into the state-space for RL algorithms. However, while these machines model the reward function, they often overlook the causal knowledge about the environment. To address this limitation, we propose the Temporal-Logic-based Causal Diagram (TL-CD) in RL, which captures the temporal causal relationships between different properties of the environment. We exploit the TL-CD to devise an RL algorithm in which an agent requires significantly less exploration of the environment. To this end, based on a TL-CD and a task DFA, we identify configurations where the agent can determine the expected rewards early during an exploration. Through a series of case studies, we demonstrate the benefits of using TL-CDs, particularly the faster convergence of the algorithm to an optimal policy due to reduced exploration of the environment.

Reinforcement Learning With Reward Machines in Stochastic Games

We investigate multi-agent reinforcement learning for stochastic games with complex tasks, where the reward functions are non-Markovian. We utilize reward machines to incorporate high-level knowledge of complex tasks. We develop an algorithm called Q-learning with reward machines for stochastic games (QRM-SG), to learn the best-response strategy at Nash equilibrium for each agent. In QRM-SG, we define the Q-function at a Nash equilibrium in augmented state space. The augmented state space integrates the state of the stochastic game and the state of reward machines. Each agent learns the Q-functions of all agents in the system. We prove that Q-functions learned in QRM-SG converge to the Q-functions at a Nash equilibrium if the stage game at each time step during learning has a global optimum point or a saddle point, and the agents update Q-functions based on the best-response strategy at this point. We use the Lemke-Howson method to derive the best-response strategy given current Q-functions. The three case studies show that QRM-SG can learn the best-response strategies effectively. QRM-SG learns the best-response strategies after around 7500 episodes in Case Study I, 1000 episodes in Case Study II, and 1500 episodes in Case Study III, while baseline methods such as Nash Q-learning and MADDPG fail to converge to the Nash equilibrium in all three case studies.

Learning Automata-Based Task Knowledge Representation from Large-Scale Generative Language Models

Automata-based representations play an important role in control and planning in sequential decision-making, but obtaining high-level task knowledge for building automata is often difficult. Although large-scale generative language models (GLMs) can help automatically distill task knowledge, the textual outputs from GLMs are not directly utilizable in sequential decision-making. We resolve this problem by proposing a novel algorithm named GLM2FSA, which obtains high-level task knowledge, represented in a finite state automaton (FSA), from a given brief description of the task goal. GLM2FSA sends queries to a GLM for task knowledge in textual form and then builds a FSA to represent the textual knowledge. This algorithm fills the gap between text and automata-based representations, and the constructed FSA can be directly utilized in sequential decision-making. We provide examples to demonstrate how GLM2FSA constructs FSAs to represent knowledge encoded in the texts generated by the large-scale GLMs.

Learning Temporal Logic Properties: an Overview of Two Recent Methods

Learning linear temporal logic (LTL) formulas from examples labeled as positive or negative has found applications in inferring descriptions of system behavior. We summarize two methods to learn LTL formulas from examples in two different problem settings. The first method assumes noise in the labeling of the examples. For that, they define the problem of inferring an LTL formula that must be consistent with most but not all of the examples. The second method considers the other problem of inferring meaningful LTL formulas in the case where only positive examples are given. Hence, the first method addresses the robustness to noise, and the second method addresses the balance between conciseness and specificity (i.e., language minimality) of the inferred formula. The summarized methods propose different algorithms to solve the aforementioned problems, as well as to infer other descriptions of temporal properties, such as signal temporal logic or deterministic finite automata.

Learning Interpretable Temporal Properties from Positive Examples Only

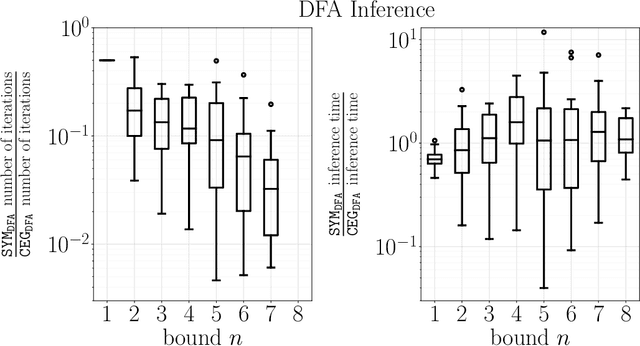
We consider the problem of explaining the temporal behavior of black-box systems using human-interpretable models. To this end, based on recent research trends, we rely on the fundamental yet interpretable models of deterministic finite automata (DFAs) and linear temporal logic (LTL) formulas. In contrast to most existing works for learning DFAs and LTL formulas, we rely on only positive examples. Our motivation is that negative examples are generally difficult to observe, in particular, from black-box systems. To learn meaningful models from positive examples only, we design algorithms that rely on conciseness and language minimality of models as regularizers. To this end, our algorithms adopt two approaches: a symbolic and a counterexample-guided one. While the symbolic approach exploits an efficient encoding of language minimality as a constraint satisfaction problem, the counterexample-guided one relies on generating suitable negative examples to prune the search. Both the approaches provide us with effective algorithms with theoretical guarantees on the learned models. To assess the effectiveness of our algorithms, we evaluate all of them on synthetic data.

Uncertainty-Aware Signal Temporal Logic Inference

Temporal logic inference is the process of extracting formal descriptions of system behaviors from data in the form of temporal logic formulas. The existing temporal logic inference methods mostly neglect uncertainties in the data, which results in limited applicability of such methods in real-world deployments. In this paper, we first investigate the uncertainties associated with trajectories of a system and represent such uncertainties in the form of interval trajectories. We then propose two uncertainty-aware signal temporal logic (STL) inference approaches to classify the undesired behaviors and desired behaviors of a system. Instead of classifying finitely many trajectories, we classify infinitely many trajectories within the interval trajectories. In the first approach, we incorporate robust semantics of STL formulas with respect to an interval trajectory to quantify the margin at which an STL formula is satisfied or violated by the interval trajectory. The second approach relies on the first learning algorithm and exploits the decision tree to infer STL formulas to classify behaviors of a given system. The proposed approaches also work for non-separable data by optimizing the worst-case robustness in inferring an STL formula. Finally, we evaluate the performance of the proposed algorithms in two case studies, where the proposed algorithms show reductions in the computation time by up to four orders of magnitude in comparison with the sampling-based baseline algorithms (for a dataset with 800 sampled trajectories in total).

Learning Linear Temporal Properties from Noisy Data: A MaxSAT Approach

We address the problem of inferring descriptions of system behavior using Linear Temporal Logic (LTL) from a finite set of positive and negative examples. Most of the existing approaches for solving such a task rely on predefined templates for guiding the structure of the inferred formula. The approaches that can infer arbitrary LTL formulas, on the other hand, are not robust to noise in the data. To alleviate such limitations, we devise two algorithms for inferring concise LTL formulas even in the presence of noise. Our first algorithm infers minimal LTL formulas by reducing the inference problem to a problem in maximum satisfiability and then using off-the-shelf MaxSAT solvers to find a solution. To the best of our knowledge, we are the first to incorporate the usage of MaxSAT solvers for inferring formulas in LTL. Our second learning algorithm relies on the first algorithm to derive a decision tree over LTL formulas based on a decision tree learning algorithm. We have implemented both our algorithms and verified that our algorithms are efficient in extracting concise LTL descriptions even in the presence of noise.