Reinforcement Learning with Temporal-Logic-Based Causal Diagrams

We study a class of reinforcement learning (RL) tasks where the objective of the agent is to accomplish temporally extended goals. In this setting, a common approach is to represent the tasks as deterministic finite automata (DFA) and integrate them into the state-space for RL algorithms. However, while these machines model the reward function, they often overlook the causal knowledge about the environment. To address this limitation, we propose the Temporal-Logic-based Causal Diagram (TL-CD) in RL, which captures the temporal causal relationships between different properties of the environment. We exploit the TL-CD to devise an RL algorithm in which an agent requires significantly less exploration of the environment. To this end, based on a TL-CD and a task DFA, we identify configurations where the agent can determine the expected rewards early during an exploration. Through a series of case studies, we demonstrate the benefits of using TL-CDs, particularly the faster convergence of the algorithm to an optimal policy due to reduced exploration of the environment.

Data-Driven Model Discrimination of Switched Nonlinear Systems with Temporal Logic Inference

This paper addresses the problem of data-driven model discrimination for unknown switched systems with unknown linear temporal logic (LTL) specifications, representing tasks, that govern their mode sequences, where only sampled data of the unknown dynamics and tasks are available. To tackle this problem, we propose data-driven methods to over-approximate the unknown dynamics and to infer the unknown specifications such that both set-membership models of the unknown dynamics and LTL formulas are guaranteed to include the ground truth model and specification/task. Moreover, we present an optimization-based algorithm for analyzing the distinguishability of a set of learned/inferred model-task pairs as well as a model discrimination algorithm for ruling out model-task pairs from this set that are inconsistent with new observations at run time. Further, we present an approach for reducing the size of inferred specifications to increase the computational efficiency of the model discrimination algorithms.

Learning Temporal Logic Properties: an Overview of Two Recent Methods

Learning linear temporal logic (LTL) formulas from examples labeled as positive or negative has found applications in inferring descriptions of system behavior. We summarize two methods to learn LTL formulas from examples in two different problem settings. The first method assumes noise in the labeling of the examples. For that, they define the problem of inferring an LTL formula that must be consistent with most but not all of the examples. The second method considers the other problem of inferring meaningful LTL formulas in the case where only positive examples are given. Hence, the first method addresses the robustness to noise, and the second method addresses the balance between conciseness and specificity (i.e., language minimality) of the inferred formula. The summarized methods propose different algorithms to solve the aforementioned problems, as well as to infer other descriptions of temporal properties, such as signal temporal logic or deterministic finite automata.

Learning Interpretable Temporal Properties from Positive Examples Only

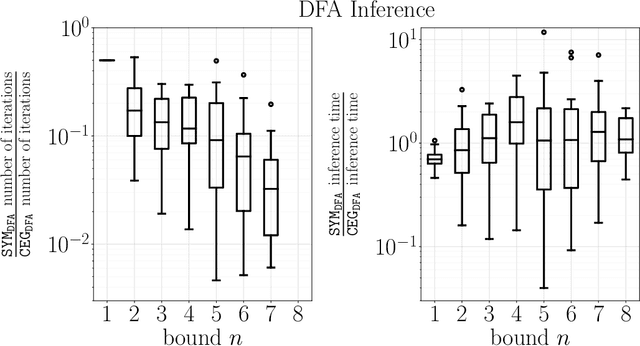
We consider the problem of explaining the temporal behavior of black-box systems using human-interpretable models. To this end, based on recent research trends, we rely on the fundamental yet interpretable models of deterministic finite automata (DFAs) and linear temporal logic (LTL) formulas. In contrast to most existing works for learning DFAs and LTL formulas, we rely on only positive examples. Our motivation is that negative examples are generally difficult to observe, in particular, from black-box systems. To learn meaningful models from positive examples only, we design algorithms that rely on conciseness and language minimality of models as regularizers. To this end, our algorithms adopt two approaches: a symbolic and a counterexample-guided one. While the symbolic approach exploits an efficient encoding of language minimality as a constraint satisfaction problem, the counterexample-guided one relies on generating suitable negative examples to prune the search. Both the approaches provide us with effective algorithms with theoretical guarantees on the learned models. To assess the effectiveness of our algorithms, we evaluate all of them on synthetic data.

Weighted Graph-Based Signal Temporal Logic Inference Using Neural Networks

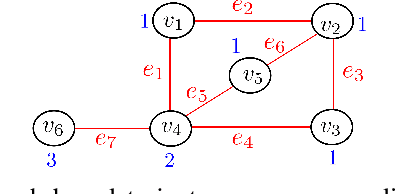
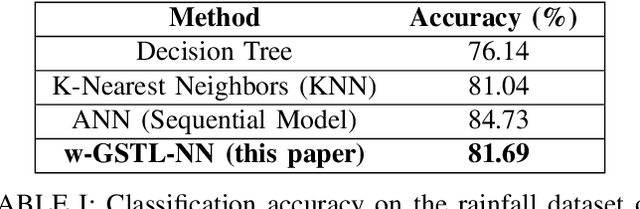
Extracting spatial-temporal knowledge from data is useful in many applications. It is important that the obtained knowledge is human-interpretable and amenable to formal analysis. In this paper, we propose a method that trains neural networks to learn spatial-temporal properties in the form of weighted graph-based signal temporal logic (wGSTL) formulas. For learning wGSTL formulas, we introduce a flexible wGSTL formula structure in which the user's preference can be applied in the inferred wGSTL formulas. In the proposed framework, each neuron of the neural networks corresponds to a subformula in a flexible wGSTL formula structure. We initially train a neural network to learn the wGSTL operators and then train a second neural network to learn the parameters in a flexible wGSTL formula structure. We use a COVID-19 dataset and a rain prediction dataset to evaluate the performance of the proposed framework and algorithms. We compare the performance of the proposed framework with three baseline classification methods including K-nearest neighbors, decision trees, and artificial neural networks. The classification accuracy obtained by the proposed framework is comparable with the baseline classification methods.

Uncertainty-Aware Signal Temporal Logic Inference

Temporal logic inference is the process of extracting formal descriptions of system behaviors from data in the form of temporal logic formulas. The existing temporal logic inference methods mostly neglect uncertainties in the data, which results in limited applicability of such methods in real-world deployments. In this paper, we first investigate the uncertainties associated with trajectories of a system and represent such uncertainties in the form of interval trajectories. We then propose two uncertainty-aware signal temporal logic (STL) inference approaches to classify the undesired behaviors and desired behaviors of a system. Instead of classifying finitely many trajectories, we classify infinitely many trajectories within the interval trajectories. In the first approach, we incorporate robust semantics of STL formulas with respect to an interval trajectory to quantify the margin at which an STL formula is satisfied or violated by the interval trajectory. The second approach relies on the first learning algorithm and exploits the decision tree to infer STL formulas to classify behaviors of a given system. The proposed approaches also work for non-separable data by optimizing the worst-case robustness in inferring an STL formula. Finally, we evaluate the performance of the proposed algorithms in two case studies, where the proposed algorithms show reductions in the computation time by up to four orders of magnitude in comparison with the sampling-based baseline algorithms (for a dataset with 800 sampled trajectories in total).