Yanbo Zhang
Revisiting 2D Foundation Models for Scalable 3D Medical Image Classification
Dec 15, 2025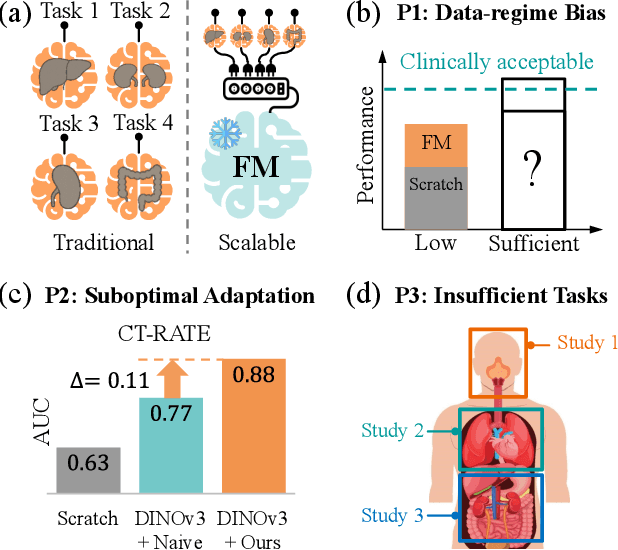
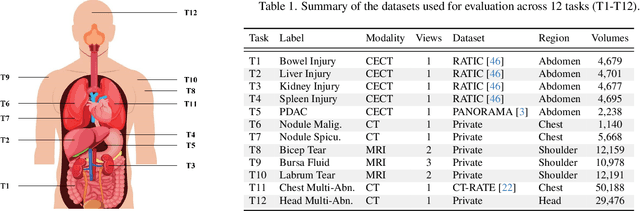
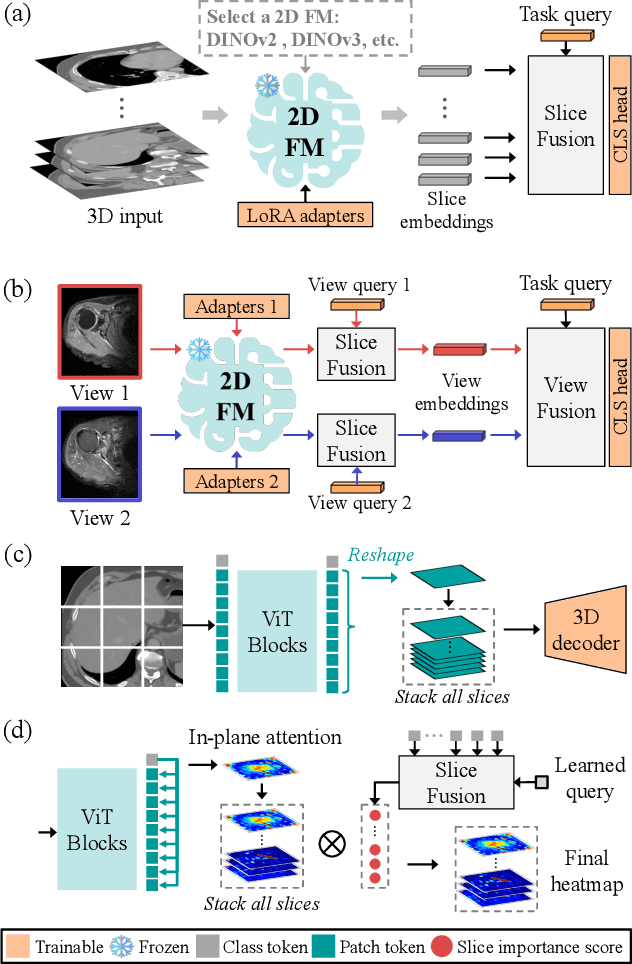
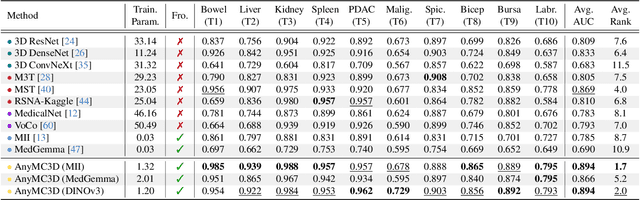
Abstract:3D medical image classification is essential for modern clinical workflows. Medical foundation models (FMs) have emerged as a promising approach for scaling to new tasks, yet current research suffers from three critical pitfalls: data-regime bias, suboptimal adaptation, and insufficient task coverage. In this paper, we address these pitfalls and introduce AnyMC3D, a scalable 3D classifier adapted from 2D FMs. Our method scales efficiently to new tasks by adding only lightweight plugins (about 1M parameters per task) on top of a single frozen backbone. This versatile framework also supports multi-view inputs, auxiliary pixel-level supervision, and interpretable heatmap generation. We establish a comprehensive benchmark of 12 tasks covering diverse pathologies, anatomies, and modalities, and systematically analyze state-of-the-art 3D classification techniques. Our analysis reveals key insights: (1) effective adaptation is essential to unlock FM potential, (2) general-purpose FMs can match medical-specific FMs if properly adapted, and (3) 2D-based methods surpass 3D architectures for 3D classification. For the first time, we demonstrate the feasibility of achieving state-of-the-art performance across diverse applications using a single scalable framework (including 1st place in the VLM3D challenge), eliminating the need for separate task-specific models.
Advancing the Scientific Method with Large Language Models: From Hypothesis to Discovery
May 22, 2025Abstract:With recent Nobel Prizes recognising AI contributions to science, Large Language Models (LLMs) are transforming scientific research by enhancing productivity and reshaping the scientific method. LLMs are now involved in experimental design, data analysis, and workflows, particularly in chemistry and biology. However, challenges such as hallucinations and reliability persist. In this contribution, we review how Large Language Models (LLMs) are redefining the scientific method and explore their potential applications across different stages of the scientific cycle, from hypothesis testing to discovery. We conclude that, for LLMs to serve as relevant and effective creative engines and productivity enhancers, their deep integration into all steps of the scientific process should be pursued in collaboration and alignment with human scientific goals, with clear evaluation metrics. The transition to AI-driven science raises ethical questions about creativity, oversight, and responsibility. With careful guidance, LLMs could evolve into creative engines, driving transformative breakthroughs across scientific disciplines responsibly and effectively. However, the scientific community must also decide how much it leaves to LLMs to drive science, even when associations with 'reasoning', mostly currently undeserved, are made in exchange for the potential to explore hypothesis and solution regions that might otherwise remain unexplored by human exploration alone.
* 45 pages
Estimating Quality in Therapeutic Conversations: A Multi-Dimensional Natural Language Processing Framework
May 09, 2025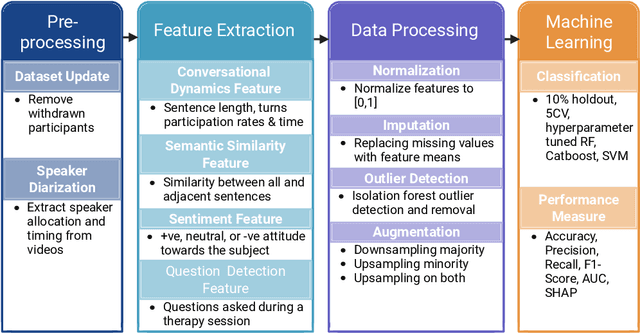
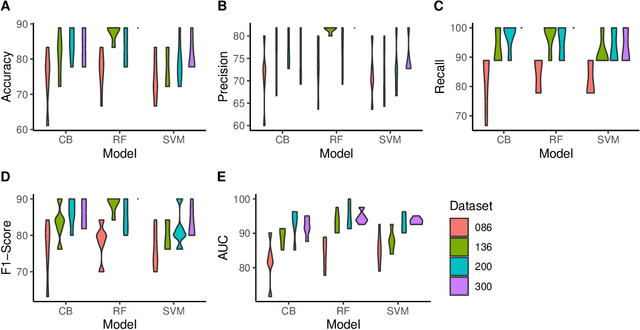
Abstract:Engagement between client and therapist is a critical determinant of therapeutic success. We propose a multi-dimensional natural language processing (NLP) framework that objectively classifies engagement quality in counseling sessions based on textual transcripts. Using 253 motivational interviewing transcripts (150 high-quality, 103 low-quality), we extracted 42 features across four domains: conversational dynamics, semantic similarity as topic alignment, sentiment classification, and question detection. Classifiers, including Random Forest (RF), Cat-Boost, and Support Vector Machines (SVM), were hyperparameter tuned and trained using a stratified 5-fold cross-validation and evaluated on a holdout test set. On balanced (non-augmented) data, RF achieved the highest classification accuracy (76.7%), and SVM achieved the highest AUC (85.4%). After SMOTE-Tomek augmentation, performance improved significantly: RF achieved up to 88.9% accuracy, 90.0% F1-score, and 94.6% AUC, while SVM reached 81.1% accuracy, 83.1% F1-score, and 93.6% AUC. The augmented data results reflect the potential of the framework in future larger-scale applications. Feature contribution revealed conversational dynamics and semantic similarity between clients and therapists were among the top contributors, led by words uttered by the client (mean and standard deviation). The framework was robust across the original and augmented datasets and demonstrated consistent improvements in F1 scores and recall. While currently text-based, the framework supports future multimodal extensions (e.g., vocal tone, facial affect) for more holistic assessments. This work introduces a scalable, data-driven method for evaluating engagement quality of the therapy session, offering clinicians real-time feedback to enhance the quality of both virtual and in-person therapeutic interactions.
Giving Simulated Cells a Voice: Evolving Prompt-to-Intervention Models for Cellular Control
May 05, 2025



Abstract:Guiding biological systems toward desired states, such as morphogenetic outcomes, remains a fundamental challenge with far-reaching implications for medicine and synthetic biology. While large language models (LLMs) have enabled natural language as an interface for interpretable control in AI systems, their use as mediators for steering biological or cellular dynamics remains largely unexplored. In this work, we present a functional pipeline that translates natural language prompts into spatial vector fields capable of directing simulated cellular collectives. Our approach combines a large language model with an evolvable neural controller (Prompt-to-Intervention, or P2I), optimized via evolutionary strategies to generate behaviors such as clustering or scattering in a simulated 2D environment. We demonstrate that even with constrained vocabulary and simplified cell models, evolved P2I networks can successfully align cellular dynamics with user-defined goals expressed in plain language. This work offers a complete loop from language input to simulated bioelectric-like intervention to behavioral output, providing a foundation for future systems capable of natural language-driven cellular control.
Understanding LLM Scientific Reasoning through Promptings and Model's Explanation on the Answers
May 02, 2025Abstract:Large language models (LLMs) have demonstrated remarkable capabilities in natural language understanding, reasoning, and problem-solving across various domains. However, their ability to perform complex, multi-step reasoning task-essential for applications in science, medicine, and law-remains an area of active investigation. This paper examines the reasoning capabilities of contemporary LLMs, analyzing their strengths, limitations, and potential for improvement. The study uses prompt engineering techniques on the Graduate-Level GoogleProof Q&A (GPQA) dataset to assess the scientific reasoning of GPT-4o. Five popular prompt engineering techniques and two tailored promptings were tested: baseline direct answer (zero-shot), chain-of-thought (CoT), zero-shot CoT, self-ask, self-consistency, decomposition, and multipath promptings. Our findings indicate that while LLMs exhibit emergent reasoning abilities, they often rely on pattern recognition rather than true logical inference, leading to inconsistencies in complex problem-solving. The results indicated that self-consistency outperformed the other prompt engineering technique with an accuracy of 52.99%, followed by direct answer (52.23%). Zero-shot CoT (50%) outperformed multipath (48.44%), decomposition (47.77%), self-ask (46.88%), and CoT (43.75%). Self-consistency performed the second worst in explaining the answers. Simple techniques such as direct answer, CoT, and zero-shot CoT have the best scientific reasoning. We propose a research agenda aimed at bridging these gaps by integrating structured reasoning frameworks, hybrid AI approaches, and human-in-the-loop methodologies. By critically evaluating the reasoning mechanisms of LLMs, this paper contributes to the ongoing discourse on the future of artificial general intelligence and the development of more robust, trustworthy AI systems.
A Non-contrast Head CT Foundation Model for Comprehensive Neuro-Trauma Triage
Feb 28, 2025



Abstract:Recent advancements in AI and medical imaging offer transformative potential in emergency head CT interpretation for reducing assessment times and improving accuracy in the face of an increasing request of such scans and a global shortage in radiologists. This study introduces a 3D foundation model for detecting diverse neuro-trauma findings with high accuracy and efficiency. Using large language models (LLMs) for automatic labeling, we generated comprehensive multi-label annotations for critical conditions. Our approach involved pretraining neural networks for hemorrhage subtype segmentation and brain anatomy parcellation, which were integrated into a pretrained comprehensive neuro-trauma detection network through multimodal fine-tuning. Performance evaluation against expert annotations and comparison with CT-CLIP demonstrated strong triage accuracy across major neuro-trauma findings, such as hemorrhage and midline shift, as well as less frequent critical conditions such as cerebral edema and arterial hyperdensity. The integration of neuro-specific features significantly enhanced diagnostic capabilities, achieving an average AUC of 0.861 for 16 neuro-trauma conditions. This work advances foundation models in medical imaging, serving as a benchmark for future AI-assisted neuro-trauma diagnostics in emergency radiology.
ProAI: Proactive Multi-Agent Conversational AI with Structured Knowledge Base for Psychiatric Diagnosis
Feb 28, 2025Abstract:Most LLM-driven conversational AI systems operate reactively, responding to user prompts without guiding the interaction. Most LLM-driven conversational AI systems operate reactively, responding to user prompts without guiding the interaction. However, many real-world applications-such as psychiatric diagnosis, consulting, and interviews-require AI to take a proactive role, asking the right questions and steering conversations toward specific objectives. Using mental health differential diagnosis as an application context, we introduce ProAI, a goal-oriented, proactive conversational AI framework. ProAI integrates structured knowledge-guided memory, multi-agent proactive reasoning, and a multi-faceted evaluation strategy, enabling LLMs to engage in clinician-style diagnostic reasoning rather than simple response generation. Through simulated patient interactions, user experience assessment, and professional clinical validation, we demonstrate that ProAI achieves up to 83.3% accuracy in mental disorder differential diagnosis while maintaining professional and empathetic interaction standards. These results highlight the potential for more reliable, adaptive, and goal-driven AI diagnostic assistants, advancing LLMs beyond reactive dialogue systems.
Heuristically Adaptive Diffusion-Model Evolutionary Strategy
Nov 20, 2024



Abstract:Diffusion Models represent a significant advancement in generative modeling, employing a dual-phase process that first degrades domain-specific information via Gaussian noise and restores it through a trainable model. This framework enables pure noise-to-data generation and modular reconstruction of, images or videos. Concurrently, evolutionary algorithms employ optimization methods inspired by biological principles to refine sets of numerical parameters encoding potential solutions to rugged objective functions. Our research reveals a fundamental connection between diffusion models and evolutionary algorithms through their shared underlying generative mechanisms: both methods generate high-quality samples via iterative refinement on random initial distributions. By employing deep learning-based diffusion models as generative models across diverse evolutionary tasks and iteratively refining diffusion models with heuristically acquired databases, we can iteratively sample potentially better-adapted offspring parameters, integrating them into successive generations of the diffusion model. This approach achieves efficient convergence toward high-fitness parameters while maintaining explorative diversity. Diffusion models introduce enhanced memory capabilities into evolutionary algorithms, retaining historical information across generations and leveraging subtle data correlations to generate refined samples. We elevate evolutionary algorithms from procedures with shallow heuristics to frameworks with deep memory. By deploying classifier-free guidance for conditional sampling at the parameter level, we achieve precise control over evolutionary search dynamics to further specific genotypical, phenotypical, or population-wide traits. Our framework marks a major heuristic and algorithmic transition, offering increased flexibility, precision, and control in evolutionary optimization processes.
Diffusion Models are Evolutionary Algorithms
Oct 03, 2024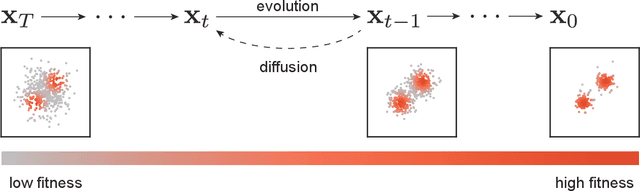
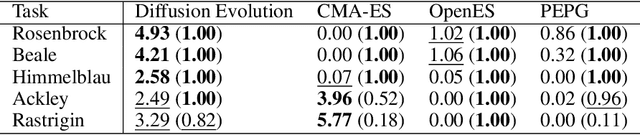
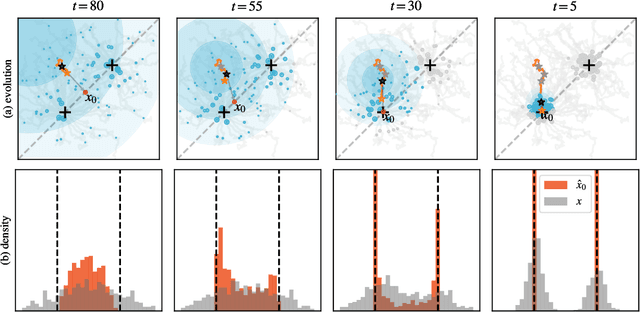

Abstract:In a convergence of machine learning and biology, we reveal that diffusion models are evolutionary algorithms. By considering evolution as a denoising process and reversed evolution as diffusion, we mathematically demonstrate that diffusion models inherently perform evolutionary algorithms, naturally encompassing selection, mutation, and reproductive isolation. Building on this equivalence, we propose the Diffusion Evolution method: an evolutionary algorithm utilizing iterative denoising -- as originally introduced in the context of diffusion models -- to heuristically refine solutions in parameter spaces. Unlike traditional approaches, Diffusion Evolution efficiently identifies multiple optimal solutions and outperforms prominent mainstream evolutionary algorithms. Furthermore, leveraging advanced concepts from diffusion models, namely latent space diffusion and accelerated sampling, we introduce Latent Space Diffusion Evolution, which finds solutions for evolutionary tasks in high-dimensional complex parameter space while significantly reducing computational steps. This parallel between diffusion and evolution not only bridges two different fields but also opens new avenues for mutual enhancement, raising questions about open-ended evolution and potentially utilizing non-Gaussian or discrete diffusion models in the context of Diffusion Evolution.
A Systematic Review on Long-Tailed Learning
Aug 01, 2024



Abstract:Long-tailed data is a special type of multi-class imbalanced data with a very large amount of minority/tail classes that have a very significant combined influence. Long-tailed learning aims to build high-performance models on datasets with long-tailed distributions, which can identify all the classes with high accuracy, in particular the minority/tail classes. It is a cutting-edge research direction that has attracted a remarkable amount of research effort in the past few years. In this paper, we present a comprehensive survey of latest advances in long-tailed visual learning. We first propose a new taxonomy for long-tailed learning, which consists of eight different dimensions, including data balancing, neural architecture, feature enrichment, logits adjustment, loss function, bells and whistles, network optimization, and post hoc processing techniques. Based on our proposed taxonomy, we present a systematic review of long-tailed learning methods, discussing their commonalities and alignable differences. We also analyze the differences between imbalance learning and long-tailed learning approaches. Finally, we discuss prospects and future directions in this field.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge