Heuristically Adaptive Diffusion-Model Evolutionary Strategy

Diffusion Models represent a significant advancement in generative modeling, employing a dual-phase process that first degrades domain-specific information via Gaussian noise and restores it through a trainable model. This framework enables pure noise-to-data generation and modular reconstruction of, images or videos. Concurrently, evolutionary algorithms employ optimization methods inspired by biological principles to refine sets of numerical parameters encoding potential solutions to rugged objective functions. Our research reveals a fundamental connection between diffusion models and evolutionary algorithms through their shared underlying generative mechanisms: both methods generate high-quality samples via iterative refinement on random initial distributions. By employing deep learning-based diffusion models as generative models across diverse evolutionary tasks and iteratively refining diffusion models with heuristically acquired databases, we can iteratively sample potentially better-adapted offspring parameters, integrating them into successive generations of the diffusion model. This approach achieves efficient convergence toward high-fitness parameters while maintaining explorative diversity. Diffusion models introduce enhanced memory capabilities into evolutionary algorithms, retaining historical information across generations and leveraging subtle data correlations to generate refined samples. We elevate evolutionary algorithms from procedures with shallow heuristics to frameworks with deep memory. By deploying classifier-free guidance for conditional sampling at the parameter level, we achieve precise control over evolutionary search dynamics to further specific genotypical, phenotypical, or population-wide traits. Our framework marks a major heuristic and algorithmic transition, offering increased flexibility, precision, and control in evolutionary optimization processes.

Diffusion Models are Evolutionary Algorithms

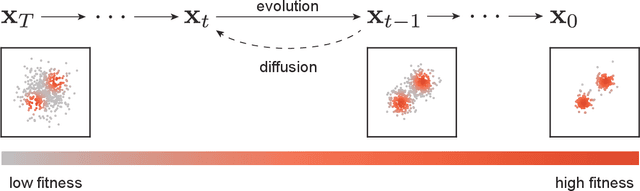
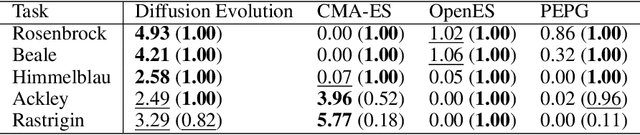
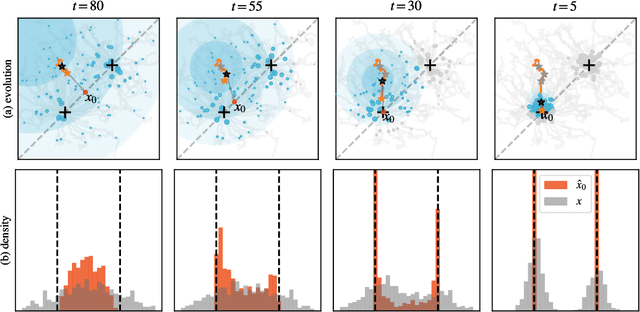
In a convergence of machine learning and biology, we reveal that diffusion models are evolutionary algorithms. By considering evolution as a denoising process and reversed evolution as diffusion, we mathematically demonstrate that diffusion models inherently perform evolutionary algorithms, naturally encompassing selection, mutation, and reproductive isolation. Building on this equivalence, we propose the Diffusion Evolution method: an evolutionary algorithm utilizing iterative denoising -- as originally introduced in the context of diffusion models -- to heuristically refine solutions in parameter spaces. Unlike traditional approaches, Diffusion Evolution efficiently identifies multiple optimal solutions and outperforms prominent mainstream evolutionary algorithms. Furthermore, leveraging advanced concepts from diffusion models, namely latent space diffusion and accelerated sampling, we introduce Latent Space Diffusion Evolution, which finds solutions for evolutionary tasks in high-dimensional complex parameter space while significantly reducing computational steps. This parallel between diffusion and evolution not only bridges two different fields but also opens new avenues for mutual enhancement, raising questions about open-ended evolution and potentially utilizing non-Gaussian or discrete diffusion models in the context of Diffusion Evolution.