Robust Multi-Robot Optimal Path Planning with Temporal Logic Constraints

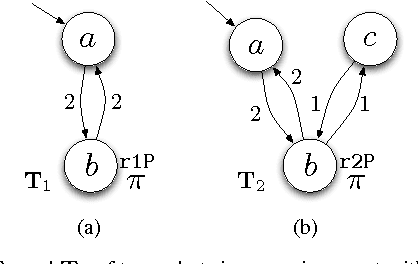
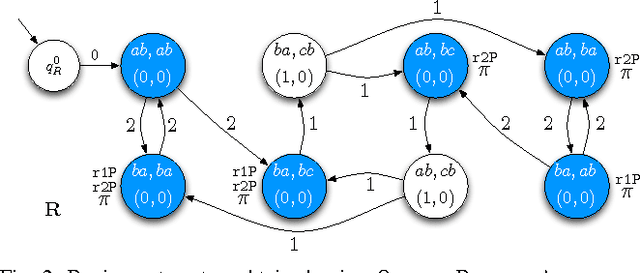
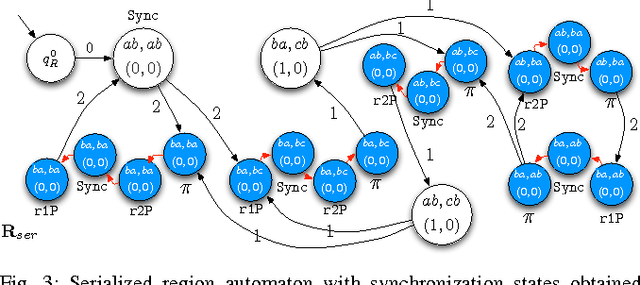
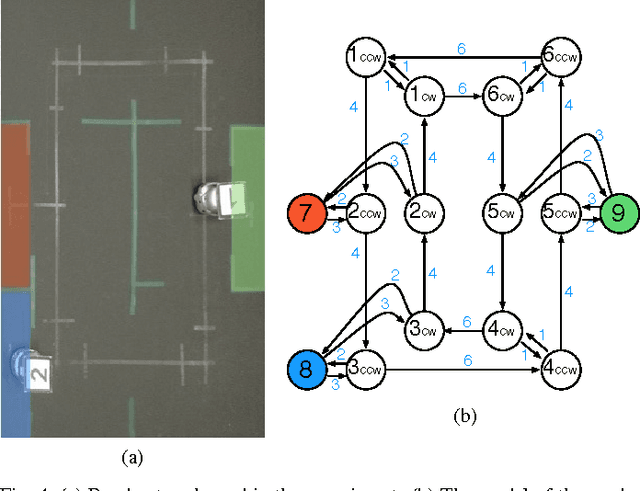
In this paper we present a method for automatically planning robust optimal paths for a group of robots that satisfy a common high level mission specification. Each robot's motion in the environment is modeled as a weighted transition system, and the mission is given as a Linear Temporal Logic (LTL) formula over a set of propositions satisfied by the regions of the environment. In addition, an optimizing proposition must repeatedly be satisfied. The goal is to minimize the maximum time between satisfying instances of the optimizing proposition while ensuring that the LTL formula is satisfied even with uncertainty in the robots' traveling times. We characterize a class of LTL formulas that are robust to robot timing errors, for which we generate optimal paths if no timing errors are present, and we present bounds on the deviation from the optimal values in the presence of errors. We implement and experimentally evaluate our method considering a persistent monitoring task in a road network environment.

Temporal Logic Motion Control using Actor-Critic Methods

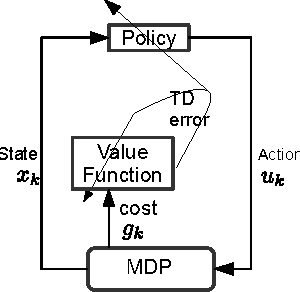
In this paper, we consider the problem of deploying a robot from a specification given as a temporal logic statement about some properties satisfied by the regions of a large, partitioned environment. We assume that the robot has noisy sensors and actuators and model its motion through the regions of the environment as a Markov Decision Process (MDP). The robot control problem becomes finding the control policy maximizing the probability of satisfying the temporal logic task on the MDP. For a large environment, obtaining transition probabilities for each state-action pair, as well as solving the necessary optimization problem for the optimal policy are usually not computationally feasible. To address these issues, we propose an approximate dynamic programming framework based on a least-square temporal difference learning method of the actor-critic type. This framework operates on sample paths of the robot and optimizes a randomized control policy with respect to a small set of parameters. The transition probabilities are obtained only when needed. Hardware-in-the-loop simulations confirm that convergence of the parameters translates to an approximately optimal policy.

An Optimal Control Approach for the Persistent Monitoring Problem

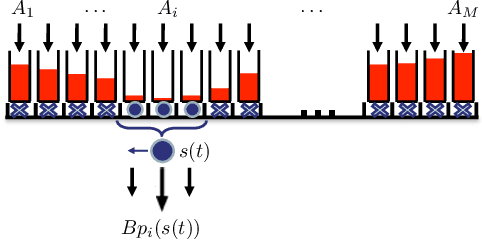
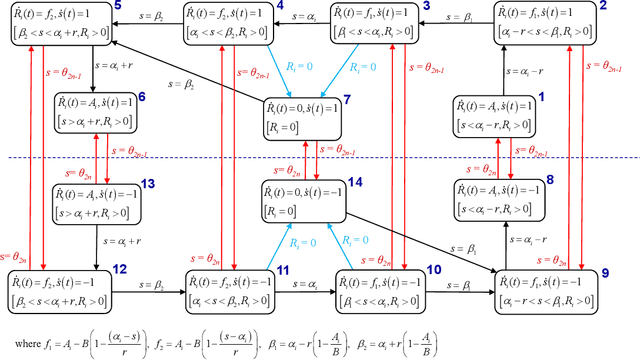
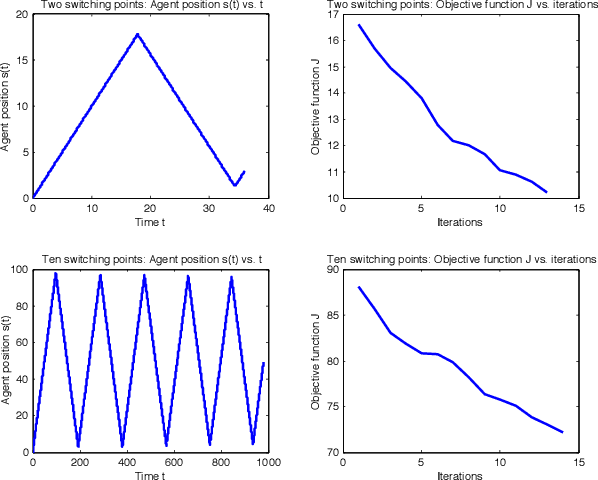
We propose an optimal control framework for persistent monitoring problems where the objective is to control the movement of mobile agents to minimize an uncertainty metric in a given mission space. For a single agent in a one-dimensional space, we show that the optimal solution is obtained in terms of a sequence of switching locations, thus reducing it to a parametric optimization problem. Using Infinitesimal Perturbation Analysis (IPA) we obtain a complete solution through a gradient-based algorithm. We also discuss a receding horizon controller which is capable of obtaining a near-optimal solution on-the-fly. We illustrate our approach with numerical examples.

Synthesis of Distributed Control and Communication Schemes from Global LTL Specifications

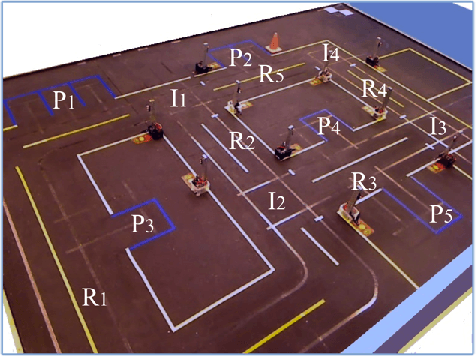
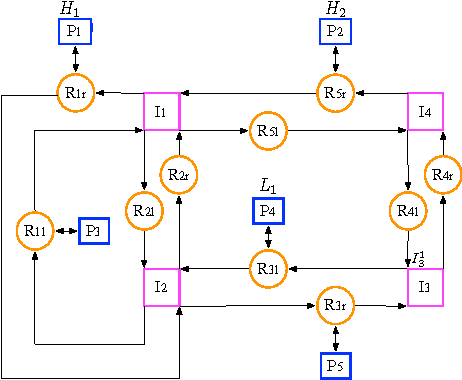
We introduce a technique for synthesis of control and communication strategies for a team of agents from a global task specification given as a Linear Temporal Logic (LTL) formula over a set of properties that can be satisfied by the agents. We consider a purely discrete scenario, in which the dynamics of each agent is modeled as a finite transition system. The proposed computational framework consists of two main steps. First, we extend results from concurrency theory to check whether the specification is distributable among the agents. Second, we generate individual control and communication strategies by using ideas from LTL model checking. We apply the method to automatically deploy a team of miniature cars in our Robotic Urban-Like Environment.

Least Squares Temporal Difference Actor-Critic Methods with Applications to Robot Motion Control

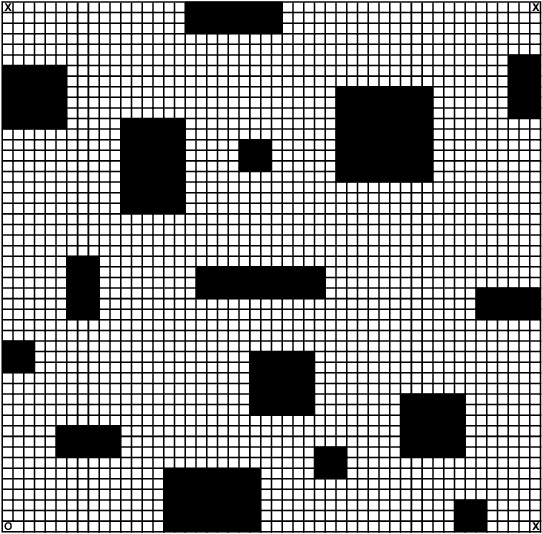
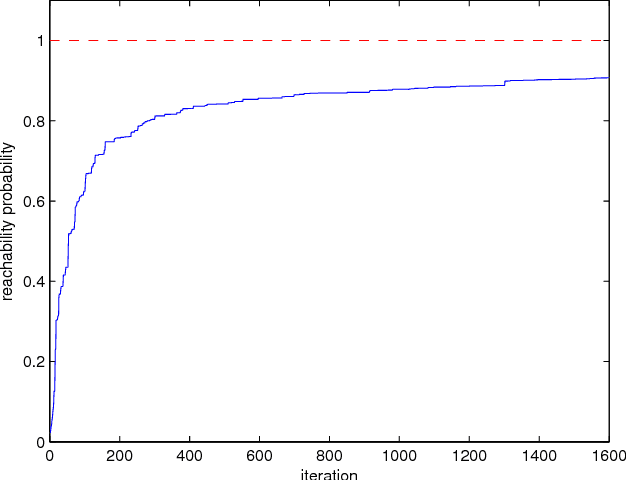
We consider the problem of finding a control policy for a Markov Decision Process (MDP) to maximize the probability of reaching some states while avoiding some other states. This problem is motivated by applications in robotics, where such problems naturally arise when probabilistic models of robot motion are required to satisfy temporal logic task specifications. We transform this problem into a Stochastic Shortest Path (SSP) problem and develop a new approximate dynamic programming algorithm to solve it. This algorithm is of the actor-critic type and uses a least-square temporal difference learning method. It operates on sample paths of the system and optimizes the policy within a pre-specified class parameterized by a parsimonious set of parameters. We show its convergence to a policy corresponding to a stationary point in the parameters' space. Simulation results confirm the effectiveness of the proposed solution.

Multi-robot Deployment From LTL Specifications with Reduced Communication

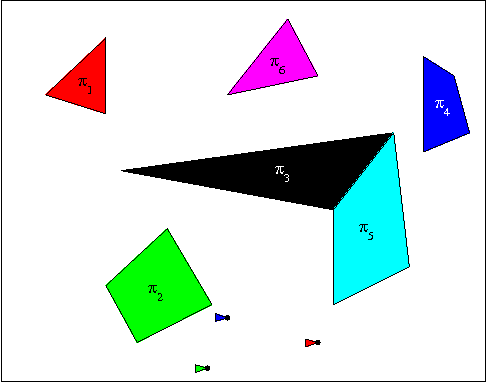
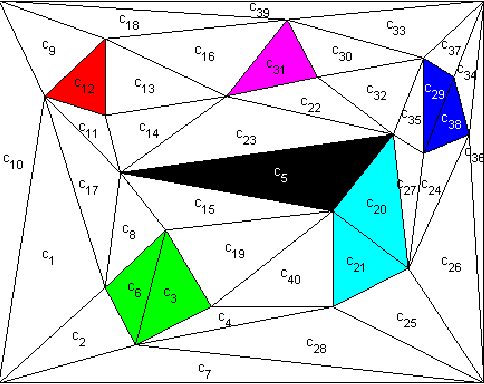
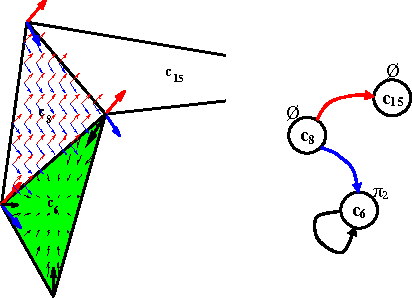
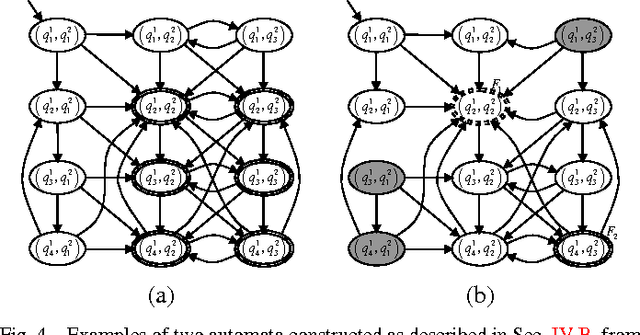
In this paper, we develop a computational framework for fully automatic deployment of a team of unicycles from a global specification given as an LTL formula over some regions of interest. Our hierarchical approach consists of four steps: (i) the construction of finite abstractions for the motions of each robot, (ii) the parallel composition of the abstractions, (iii) the generation of a satisfying motion of the team; (iv) mapping this motion to individual robot control and communication strategies. The main result of the paper is an algorithm to reduce the amount of inter-robot communication during the fourth step of the procedure.

Optimal Multi-Robot Path Planning with Temporal Logic Constraints

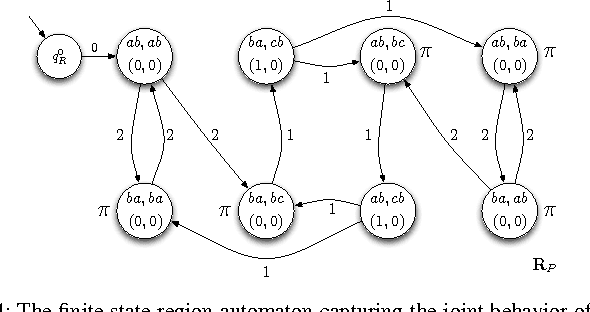
In this paper we present a method for automatically planning optimal paths for a group of robots that satisfy a common high level mission specification. Each robot's motion in the environment is modeled as a weighted transition system. The mission is given as a Linear Temporal Logic formula. In addition, an optimizing proposition must repeatedly be satisfied. The goal is to minimize the maximum time between satisfying instances of the optimizing proposition. Our method is guaranteed to compute an optimal set of robot paths. We utilize a timed automaton representation in order to capture the relative position of the robots in the environment. We then obtain a bisimulation of this timed automaton as a finite transition system that captures the joint behavior of the robots and apply our earlier algorithm for the single robot case to optimize the group motion. We present a simulation of a persistent monitoring task in a road network environment.

LTL Control in Uncertain Environments with Probabilistic Satisfaction Guarantees

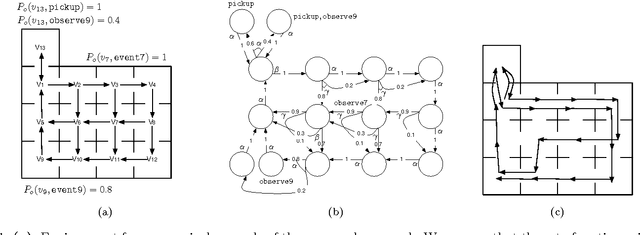
We present a method to generate a robot control strategy that maximizes the probability to accomplish a task. The task is given as a Linear Temporal Logic (LTL) formula over a set of properties that can be satisfied at the regions of a partitioned environment. We assume that the probabilities with which the properties are satisfied at the regions are known, and the robot can determine the truth value of a proposition only at the current region. Motivated by several results on partitioned-based abstractions, we assume that the motion is performed on a graph. To account for noisy sensors and actuators, we assume that a control action enables several transitions with known probabilities. We show that this problem can be reduced to the problem of generating a control policy for a Markov Decision Process (MDP) such that the probability of satisfying an LTL formula over its states is maximized. We provide a complete solution for the latter problem that builds on existing results from probabilistic model checking. We include an illustrative case study.

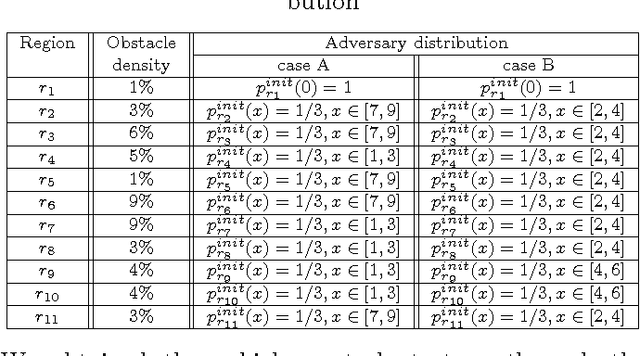
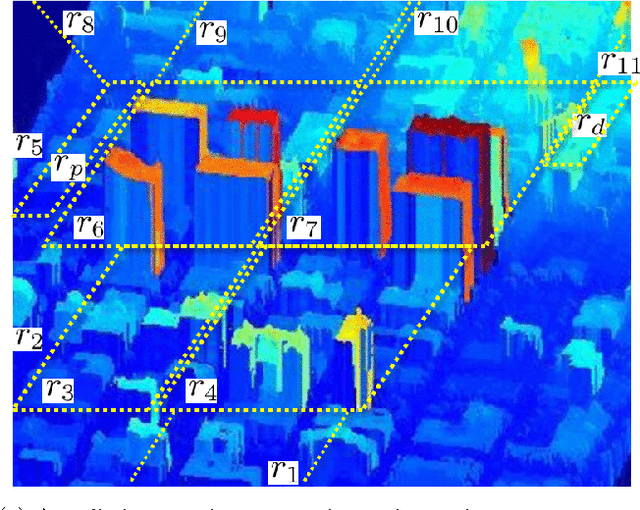
Probabilistically Safe Vehicle Control in a Hostile Environment

In this paper we present an approach to control a vehicle in a hostile environment with static obstacles and moving adversaries. The vehicle is required to satisfy a mission objective expressed as a temporal logic specification over a set of properties satisfied at regions of a partitioned environment. We model the movements of adversaries in between regions of the environment as Poisson processes. Furthermore, we assume that the time it takes for the vehicle to traverse in between two facets of each region is exponentially distributed, and we obtain the rate of this exponential distribution from a simulator of the environment. We capture the motion of the vehicle and the vehicle updates of adversaries distributions as a Markov Decision Process. Using tools in Probabilistic Computational Tree Logic, we find a control strategy for the vehicle that maximizes the probability of accomplishing the mission objective. We demonstrate our approach with illustrative case studies.

MDP Optimal Control under Temporal Logic Constraints

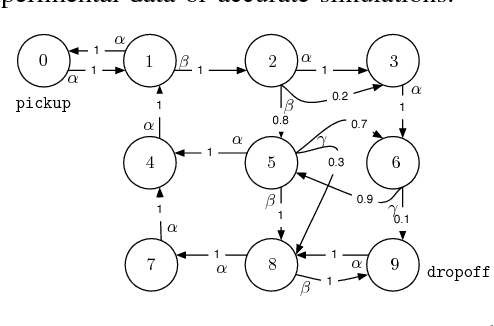
In this paper, we develop a method to automatically generate a control policy for a dynamical system modeled as a Markov Decision Process (MDP). The control specification is given as a Linear Temporal Logic (LTL) formula over a set of propositions defined on the states of the MDP. We synthesize a control policy such that the MDP satisfies the given specification almost surely, if such a policy exists. In addition, we designate an "optimizing proposition" to be repeatedly satisfied, and we formulate a novel optimization criterion in terms of minimizing the expected cost in between satisfactions of this proposition. We propose a sufficient condition for a policy to be optimal, and develop a dynamic programming algorithm that synthesizes a policy that is optimal under some conditions, and sub-optimal otherwise. This problem is motivated by robotic applications requiring persistent tasks, such as environmental monitoring or data gathering, to be performed.