Probabilistically Safe Vehicle Control in a Hostile Environment
Paper and Code
Mar 24, 2011
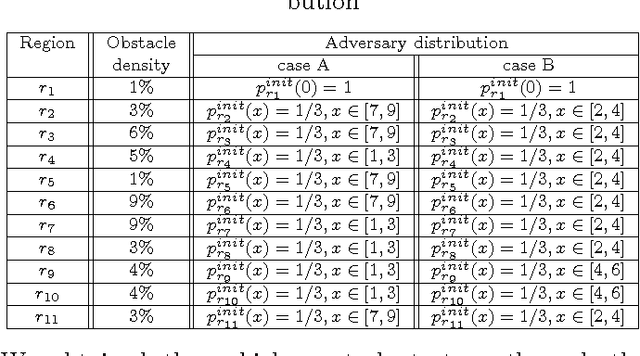
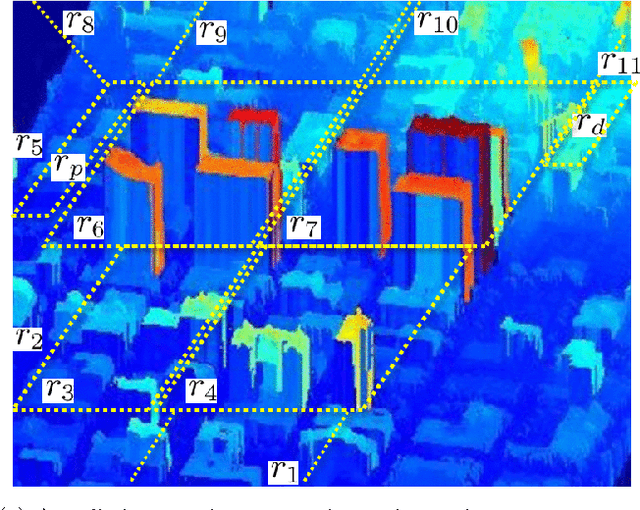

In this paper we present an approach to control a vehicle in a hostile environment with static obstacles and moving adversaries. The vehicle is required to satisfy a mission objective expressed as a temporal logic specification over a set of properties satisfied at regions of a partitioned environment. We model the movements of adversaries in between regions of the environment as Poisson processes. Furthermore, we assume that the time it takes for the vehicle to traverse in between two facets of each region is exponentially distributed, and we obtain the rate of this exponential distribution from a simulator of the environment. We capture the motion of the vehicle and the vehicle updates of adversaries distributions as a Markov Decision Process. Using tools in Probabilistic Computational Tree Logic, we find a control strategy for the vehicle that maximizes the probability of accomplishing the mission objective. We demonstrate our approach with illustrative case studies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge