Negotiating the Probabilistic Satisfaction of Temporal Logic Motion Specifications

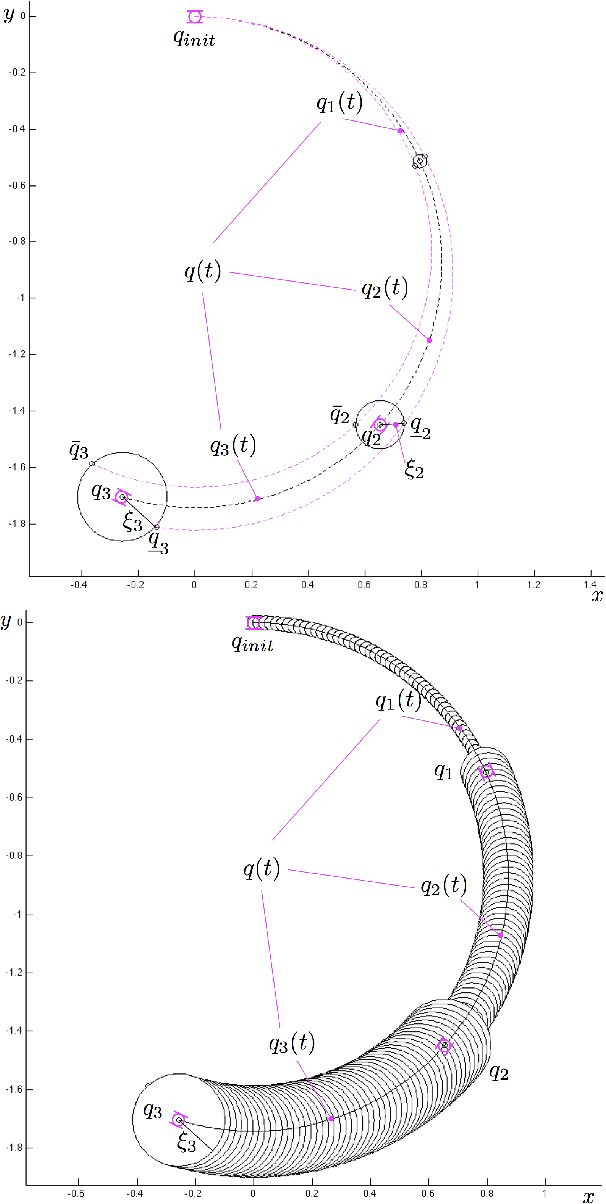
We propose a human-supervised control synthesis method for a stochastic Dubins vehicle such that the probability of satisfying a specification given as a formula in a fragment of Probabilistic Computational Tree Logic (PCTL) over a set of environmental properties is maximized. Under some mild assumptions, we construct a finite approximation for the motion of the vehicle in the form of a tree-structured Markov Decision Process (MDP). We introduce an efficient algorithm, which exploits the tree structure of the MDP, for synthesizing a control policy that maximizes the probability of satisfaction. For the proposed PCTL fragment, we define the specification update rules that guarantee the increase (or decrease) of the satisfaction probability. We introduce an incremental algorithm for synthesizing an updated MDP control policy that reuses the initial solution. The initial specification can be updated, using the rules, until the supervisor is satisfied with both the updated specification and the corresponding satisfaction probability. We propose an offline and an online application of this method.

Control of Noisy Differential-Drive Vehicles from Time-Bounded Temporal Logic Specifications

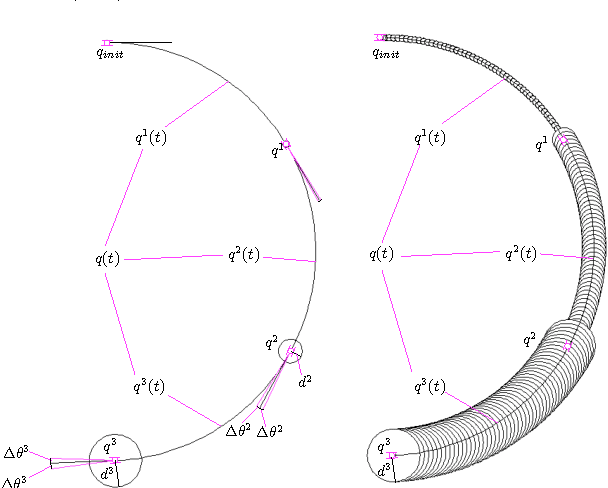
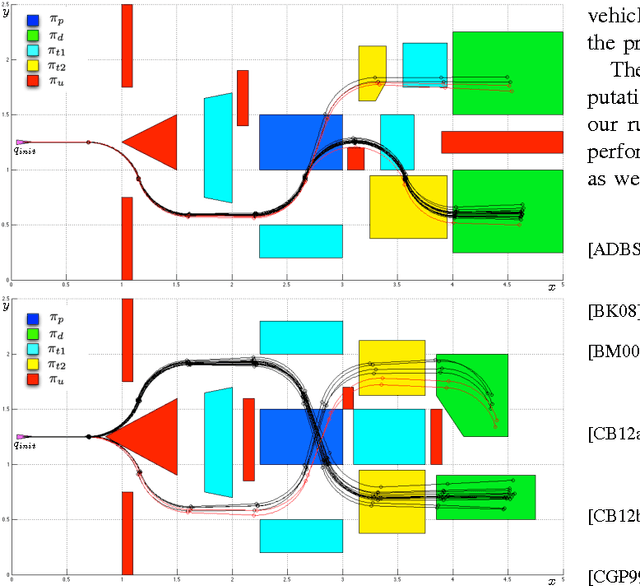
We address the problem of controlling a noisy differential drive mobile robot such that the probability of satisfying a specification given as a Bounded Linear Temporal Logic (BLTL) formula over a set of properties at the regions in the environment is maximized. We assume that the vehicle can determine its precise initial position in a known map of the environment. However, inspired by practical limitations, we assume that the vehicle is equipped with noisy actuators and, during its motion in the environment, it can only measure the angular velocity of its wheels using limited accuracy incremental encoders. Assuming the duration of the motion is finite, we map the measurements to a Markov Decision Process (MDP). We use recent results in Statistical Model Checking (SMC) to obtain an MDP control policy that maximizes the probability of satisfaction. We translate this policy to a vehicle feedback control strategy and show that the probability that the vehicle satisfies the specification in the environment is bounded from below by the probability of satisfying the specification on the MDP. We illustrate our method with simulations and experimental results.

Probabilistically Safe Control of Noisy Dubins Vehicles

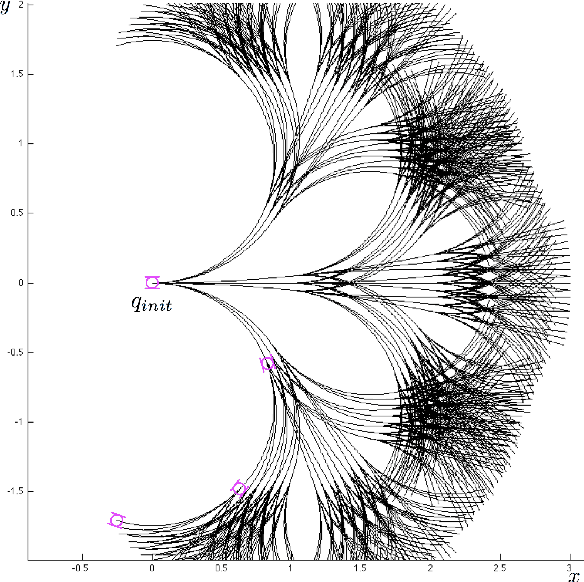
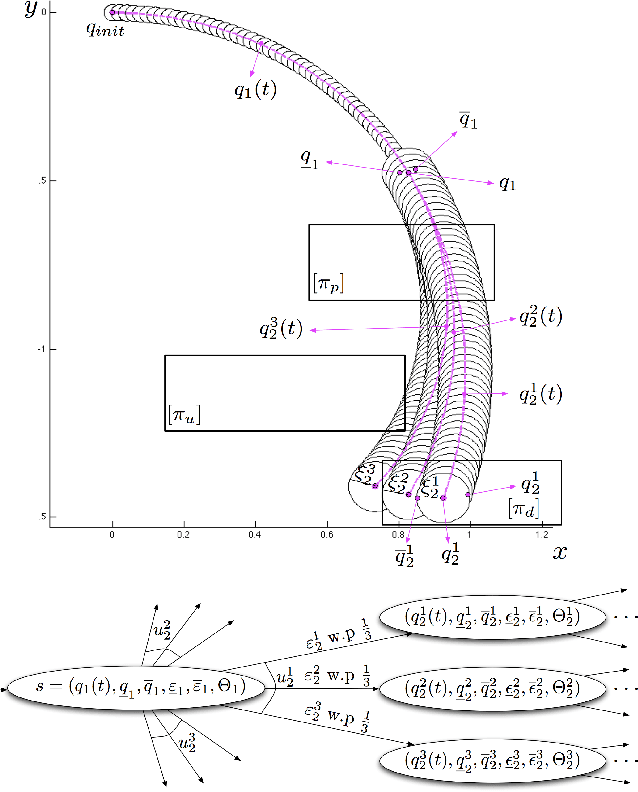
We address the problem of controlling a stochastic version of a Dubins vehicle such that the probability of satisfying a temporal logic specification over a set of properties at the regions in a partitioned environment is maximized. We assume that the vehicle can determine its precise initial position in a known map of the environment. However, inspired by practical limitations, we assume that the vehicle is equipped with noisy actuators and, during its motion in the environment, it can only measure its angular velocity using a limited accuracy gyroscope. Through quantization and discretization, we construct a finite approximation for the motion of the vehicle in the form of a Markov Decision Process (MDP). We allow for task specifications given as temporal logic statements over the environmental properties, and use tools in Probabilistic Computation Tree Logic (PCTL) to generate an MDP control policy that maximizes the probability of satisfaction. We translate this policy to a vehicle feedback control strategy and show that the probability that the vehicle satisfies the specification in the original environment is bounded from below by the maximum probability of satisfying the specification on the MDP.

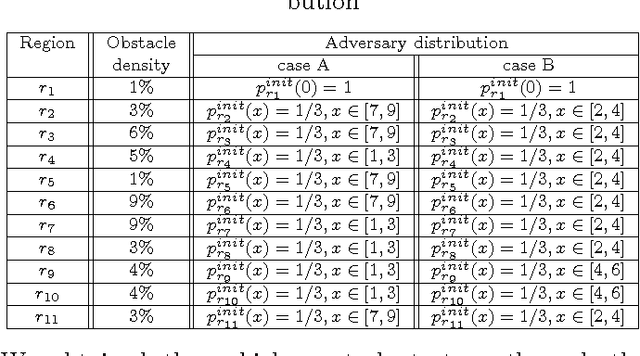
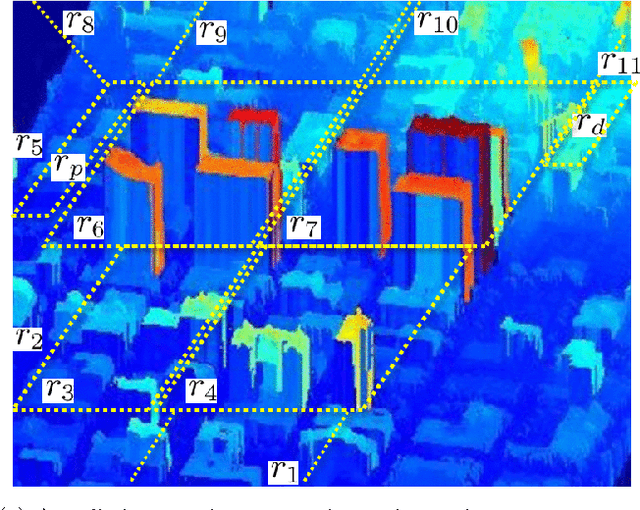
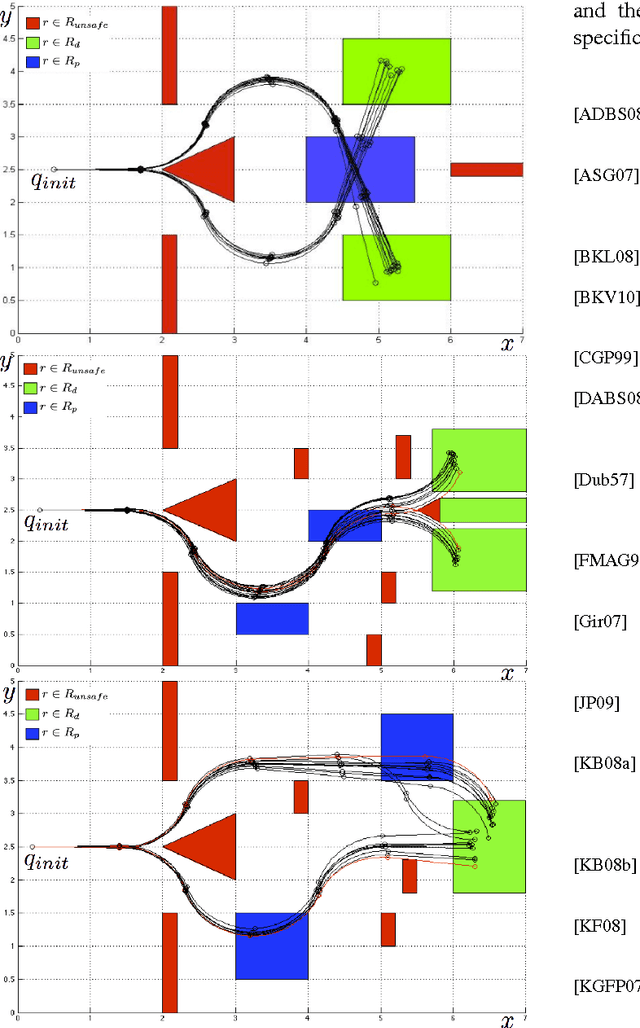
Probabilistically Safe Vehicle Control in a Hostile Environment

In this paper we present an approach to control a vehicle in a hostile environment with static obstacles and moving adversaries. The vehicle is required to satisfy a mission objective expressed as a temporal logic specification over a set of properties satisfied at regions of a partitioned environment. We model the movements of adversaries in between regions of the environment as Poisson processes. Furthermore, we assume that the time it takes for the vehicle to traverse in between two facets of each region is exponentially distributed, and we obtain the rate of this exponential distribution from a simulator of the environment. We capture the motion of the vehicle and the vehicle updates of adversaries distributions as a Markov Decision Process. Using tools in Probabilistic Computational Tree Logic, we find a control strategy for the vehicle that maximizes the probability of accomplishing the mission objective. We demonstrate our approach with illustrative case studies.