Auxiliary-Adaptive Control Barrier Functions for Safety Critical Systems

This paper studies safety guarantees for systems with time-varying control bounds. It has been shown that optimizing quadratic costs subject to state and control constraints can be reduced to a sequence of Quadratic Programs (QPs) using Control Barrier Functions (CBFs). One of the main challenges in this method is that the CBF-based QP could easily become infeasible under tight control bounds, especially when the control bounds are time-varying. The recently proposed adaptive CBFs have addressed such infeasibility issues, but require extensive and non-trivial hyperparameter tuning for the CBF-based QP and may introduce overshooting control near the boundaries of safe sets. To address these issues, we propose a new type of adaptive CBFs called Auxiliary Variable CBFs (AVCBFs). Specifically, we introduce an auxiliary variable that multiplies each CBF itself, and define dynamics for the auxiliary variable to adapt it in constructing the corresponding CBF constraint. In this way, we can improve the feasibility of the CBF-based QP while avoiding extensive parameter tuning with non-overshooting control since the formulation is identical to classical CBF methods. We demonstrate the advantages of using AVCBFs and compare them with existing techniques on an Adaptive Cruise Control (ACC) problem with time-varying control bounds.

Learning Feasibility Constraints for Control Barrier Functions

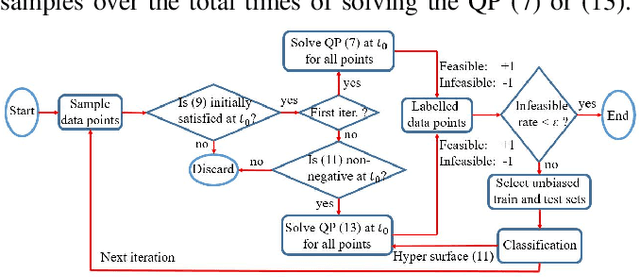
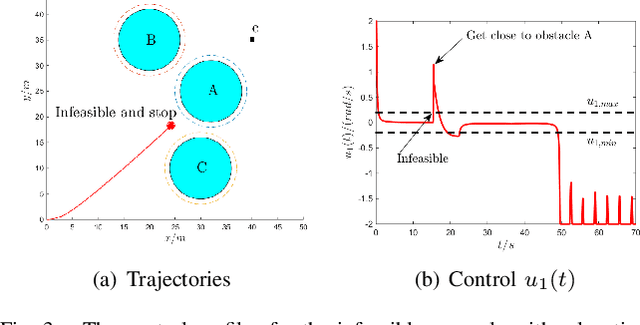
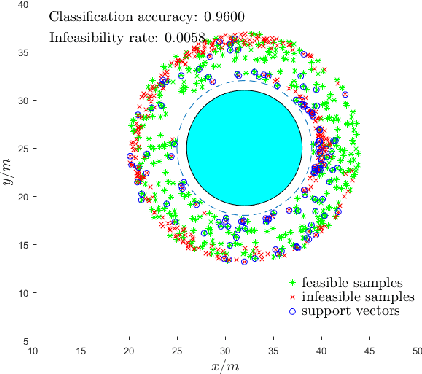
It has been shown that optimizing quadratic costs while stabilizing affine control systems to desired (sets of) states subject to state and control constraints can be reduced to a sequence of Quadratic Programs (QPs) by using Control Barrier Functions (CBFs) and Control Lyapunov Functions (CLFs). In this paper, we employ machine learning techniques to ensure the feasibility of these QPs, which is a challenging problem, especially for high relative degree constraints where High Order CBFs (HOCBFs) are required. To this end, we propose a sampling-based learning approach to learn a new feasibility constraint for CBFs; this constraint is then enforced by another HOCBF added to the QPs. The accuracy of the learned feasibility constraint is recursively improved by a recurrent training algorithm. We demonstrate the advantages of the proposed learning approach to constrained optimal control problems with specific focus on a robot control problem and on autonomous driving in an unknown environment.

Iterative Convex Optimization for Model Predictive Control with Discrete-Time High-Order Control Barrier Functions

Safety is one of the fundamental challenges in control theory. Recently, multi-step optimal control problems for discrete-time dynamical systems were formulated to enforce stability, while subject to input constraints as well as safety-critical requirements using discrete-time control barrier functions within a model predictive control (MPC) framework. Existing work usually focus on the feasibility or the safety for the optimization problem, and the majority of the existing work restrict the discussions to relative-degree one for control barrier function. Additionally, the real-time computation is challenging when a large horizon is considered in the MPC problem for relative-degree one or high-order control barrier functions. In this paper, we propose a framework that solves the safety-critical MPC problem in an iterative optimization, which is applicable for any relative-degree control barrier functions. In the proposed formulation, the nonlinear system dynamics as well as the safety constraints modeled as discrete-time high-order control barrier functions (DHOCBF) are linearized at each time step. Our formulation is generally valid for any control barrier function with an arbitrary relative-degree. The advantages of fast computational performance with safety guarantee are analyzed and validated with numerical results.

Control Barrier Functions for Systems with Multiple Control Inputs

Control Barrier Functions (CBFs) are becoming popular tools in guaranteeing safety for nonlinear systems and constraints, and they can reduce a constrained optimal control problem into a sequence of Quadratic Programs (QPs) for affine control systems. The recently proposed High Order Control Barrier Functions (HOCBFs) work for arbitrary relative degree constraints. One of the challenges in a HOCBF is to address the relative degree problem when a system has multiple control inputs, i.e., the relative degree could be defined with respect to different components of the control vector. This paper proposes two methods for HOCBFs to deal with systems with multiple control inputs: a general integral control method and a method which is simpler but limited to specific classes of physical systems. When control bounds are involved, the feasibility of the above mentioned QPs can also be significantly improved with the proposed methods. We illustrate our approaches on a unicyle model with two control inputs, and compare the two proposed methods to demonstrate their effectiveness and performance.

High Order Control Lyapunov-Barrier Functions for Temporal Logic Specifications

Recent work has shown that stabilizing an affine control system to a desired state while optimizing a quadratic cost subject to state and control constraints can be reduced to a sequence of Quadratic Programs (QPs) by using Control Barrier Functions (CBFs) and Control Lyapunov Functions (CLFs). In our own recent work, we defined High Order CBFs (HOCBFs) for systems and constraints with arbitrary relative degrees. In this paper, in order to accommodate initial states that do not satisfy the state constraints and constraints with arbitrary relative degree, we generalize HOCBFs to High Order Control Lyapunov-Barrier Functions (HOCLBFs). We also show that the proposed HOCLBFs can be used to guarantee the Boolean satisfaction of Signal Temporal Logic (STL) formulae over the state of the system. We illustrate our approach on a safety-critical optimal control problem (OCP) for a unicycle.

Bridging the Gap between Optimal Trajectory Planning and Safety-Critical Control with Applications to Autonomous Vehicles

We address the problem of optimizing the performance of a dynamic system while satisfying hard safety constraints at all times. Implementing an optimal control solution is limited by the computational cost required to derive it in real time, especially when constraints become active, as well as the need to rely on simple linear dynamics, simple objective functions, and ignoring noise. The recently proposed Control Barrier Function (CBF) method may be used for safety-critical control at the expense of sub-optimal performance. In this paper, we develop a real-time control framework that combines optimal trajectories generated through optimal control with the computationally efficient CBF method providing safety guarantees. We use Hamiltonian analysis to obtain a tractable optimal solution for a linear or linearized system, then employ High Order CBFs (HOCBFs) and Control Lyapunov Functions (CLFs) to account for constraints with arbitrary relative degrees and to track the optimal state, respectively. We further show how to deal with noise in arbitrary relative degree systems. The proposed framework is then applied to the optimal traffic merging problem for Connected and Automated Vehicles (CAVs) where the objective is to jointly minimize the travel time and energy consumption of each CAV subject to speed, acceleration, and speed-dependent safety constraints. In addition, when considering more complex objective functions, nonlinear dynamics and passenger comfort requirements for which analytical optimal control solutions are unavailable, we adapt the HOCBF method to such problems. Simulation examples are included to compare the performance of the proposed framework to optimal solutions (when available) and to a baseline provided by human-driven vehicles with results showing significant improvements in all metrics.

Feasibility-Guided Learning for Robust Control in Constrained Optimal Control Problems

Optimal control problems with constraints ensuring safety and convergence to desired states can be mapped onto a sequence of real time optimization problems through the use of Control Barrier Functions (CBFs) and Control Lyapunov Functions (CLFs). One of the main challenges in these approaches is ensuring the feasibility of the resulting quadratic programs (QPs) if the system is affine in controls. The recently proposed penalty method has the potential to improve the existence of feasible solutions to such problems. In this paper, we further improve the feasibility robustness (i.e., feasibility maintenance in the presence of time-varying and unknown unsafe sets) through the definition of a High Order CBF (HOCBF) that works for arbitrary relative degree constraints; this is achieved by a proposed feasibility-guided learning approach. Specifically, we apply machine learning techniques to classify the parameter space of a HOCBF into feasible and infeasible sets, and get a differentiable classifier that is then added to the learning process. The proposed feasibility-guided learning approach is compared with the gradient-descent method on a robot control problem. The simulation results show an improved ability of the feasibility-guided learning approach over the gradient-decent method to determine the optimal parameters in the definition of a HOCBF for the feasibility robustness, as well as show the potential of the CBF method for robot safe navigation in an unknown environment.

Temporal Logic Motion Control using Actor-Critic Methods

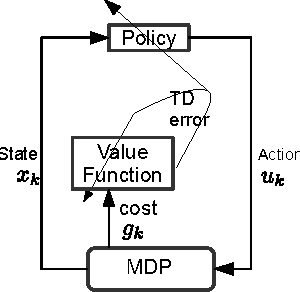
In this paper, we consider the problem of deploying a robot from a specification given as a temporal logic statement about some properties satisfied by the regions of a large, partitioned environment. We assume that the robot has noisy sensors and actuators and model its motion through the regions of the environment as a Markov Decision Process (MDP). The robot control problem becomes finding the control policy maximizing the probability of satisfying the temporal logic task on the MDP. For a large environment, obtaining transition probabilities for each state-action pair, as well as solving the necessary optimization problem for the optimal policy are usually not computationally feasible. To address these issues, we propose an approximate dynamic programming framework based on a least-square temporal difference learning method of the actor-critic type. This framework operates on sample paths of the robot and optimizes a randomized control policy with respect to a small set of parameters. The transition probabilities are obtained only when needed. Hardware-in-the-loop simulations confirm that convergence of the parameters translates to an approximately optimal policy.

Least Squares Temporal Difference Actor-Critic Methods with Applications to Robot Motion Control

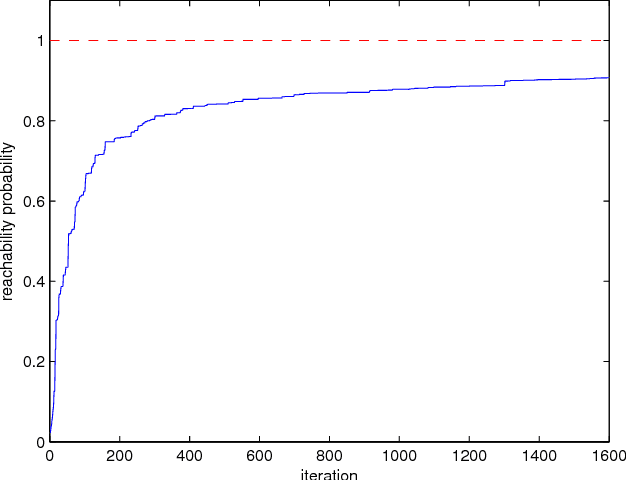
We consider the problem of finding a control policy for a Markov Decision Process (MDP) to maximize the probability of reaching some states while avoiding some other states. This problem is motivated by applications in robotics, where such problems naturally arise when probabilistic models of robot motion are required to satisfy temporal logic task specifications. We transform this problem into a Stochastic Shortest Path (SSP) problem and develop a new approximate dynamic programming algorithm to solve it. This algorithm is of the actor-critic type and uses a least-square temporal difference learning method. It operates on sample paths of the system and optimizes the policy within a pre-specified class parameterized by a parsimonious set of parameters. We show its convergence to a policy corresponding to a stationary point in the parameters' space. Simulation results confirm the effectiveness of the proposed solution.