Learning Feasibility Constraints for Control Barrier Functions
Paper and Code
Mar 10, 2023
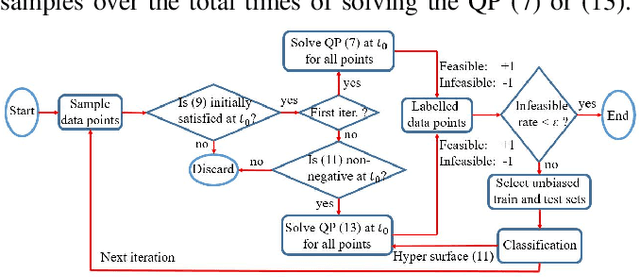
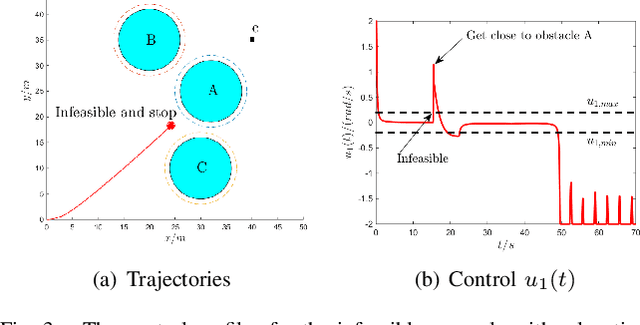
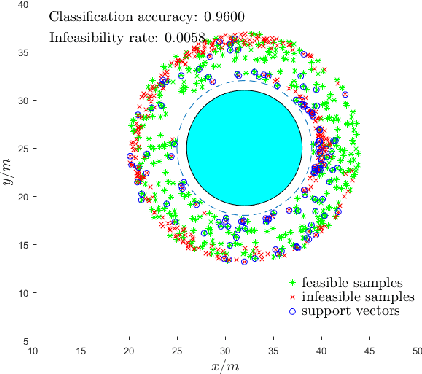
It has been shown that optimizing quadratic costs while stabilizing affine control systems to desired (sets of) states subject to state and control constraints can be reduced to a sequence of Quadratic Programs (QPs) by using Control Barrier Functions (CBFs) and Control Lyapunov Functions (CLFs). In this paper, we employ machine learning techniques to ensure the feasibility of these QPs, which is a challenging problem, especially for high relative degree constraints where High Order CBFs (HOCBFs) are required. To this end, we propose a sampling-based learning approach to learn a new feasibility constraint for CBFs; this constraint is then enforced by another HOCBF added to the QPs. The accuracy of the learned feasibility constraint is recursively improved by a recurrent training algorithm. We demonstrate the advantages of the proposed learning approach to constrained optimal control problems with specific focus on a robot control problem and on autonomous driving in an unknown environment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge