Temporal Logic Motion Control using Actor-Critic Methods
Paper and Code
Feb 23, 2012

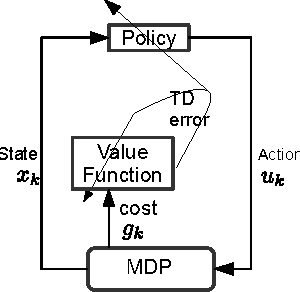

In this paper, we consider the problem of deploying a robot from a specification given as a temporal logic statement about some properties satisfied by the regions of a large, partitioned environment. We assume that the robot has noisy sensors and actuators and model its motion through the regions of the environment as a Markov Decision Process (MDP). The robot control problem becomes finding the control policy maximizing the probability of satisfying the temporal logic task on the MDP. For a large environment, obtaining transition probabilities for each state-action pair, as well as solving the necessary optimization problem for the optimal policy are usually not computationally feasible. To address these issues, we propose an approximate dynamic programming framework based on a least-square temporal difference learning method of the actor-critic type. This framework operates on sample paths of the robot and optimizes a randomized control policy with respect to a small set of parameters. The transition probabilities are obtained only when needed. Hardware-in-the-loop simulations confirm that convergence of the parameters translates to an approximately optimal policy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge