Optimal Multi-Robot Path Planning with LTL Constraints: Guaranteeing Correctness Through Synchronization

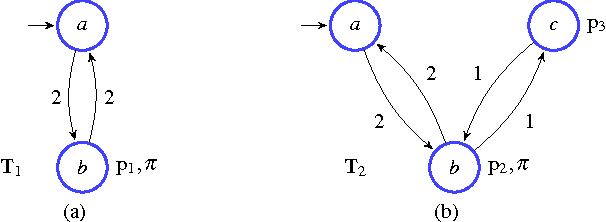
In this paper, we consider the automated planning of optimal paths for a robotic team satisfying a high level mission specification. Each robot in the team is modeled as a weighted transition system where the weights have associated deviation values that capture the non-determinism in the traveling times of the robot during its deployment. The mission is given as a Linear Temporal Logic (LTL) formula over a set of propositions satisfied at the regions of the environment. Additionally, we have an optimizing proposition capturing some particular task that must be repeatedly completed by the team. The goal is to minimize the maximum time between successive satisfying instances of the optimizing proposition while guaranteeing that the mission is satisfied even under non-deterministic traveling times. Our method relies on the communication capabilities of the robots to guarantee correctness and maintain performance during deployment. After computing a set of optimal satisfying paths for the members of the team, we also compute a set of synchronization sequences for each robot to ensure that the LTL formula is never violated during deployment. We implement and experimentally evaluate our method considering a persistent monitoring task in a road network environment.

Incremental Control Synthesis in Probabilistic Environments with Temporal Logic Constraints

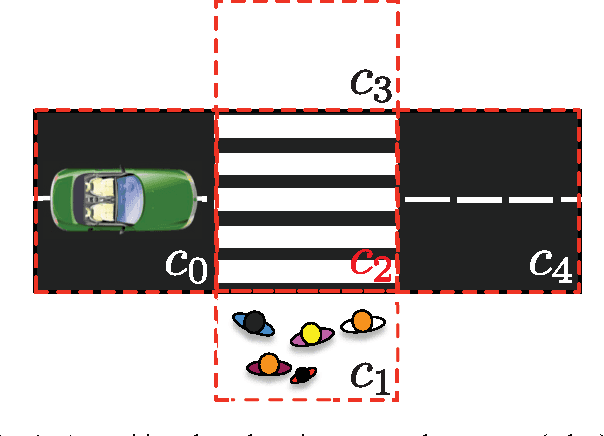
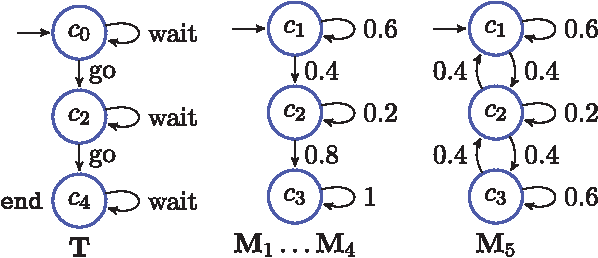
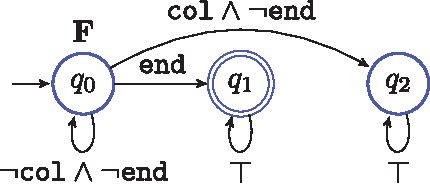
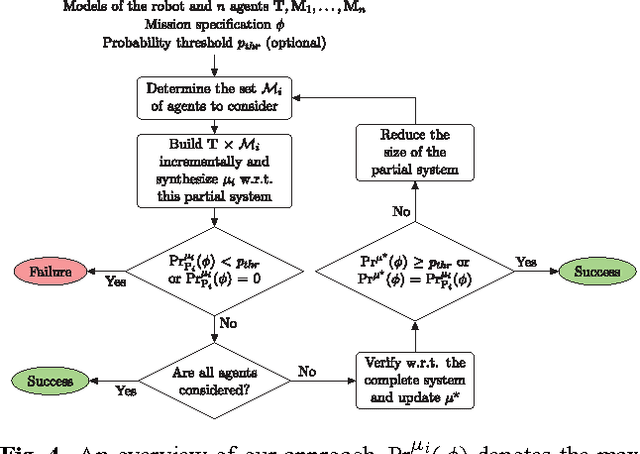
In this paper, we present a method for optimal control synthesis of a plant that interacts with a set of agents in a graph-like environment. The control specification is given as a temporal logic statement about some properties that hold at the vertices of the environment. The plant is assumed to be deterministic, while the agents are probabilistic Markov models. The goal is to control the plant such that the probability of satisfying a syntactically co-safe Linear Temporal Logic formula is maximized. We propose a computationally efficient incremental approach based on the fact that temporal logic verification is computationally cheaper than synthesis. We present a case-study where we compare our approach to the classical non-incremental approach in terms of computation time and memory usage.

Robust Multi-Robot Optimal Path Planning with Temporal Logic Constraints

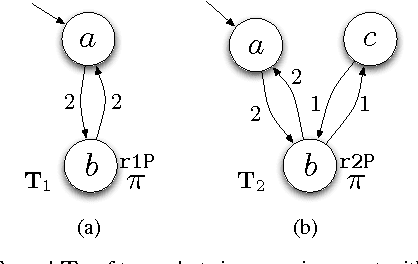
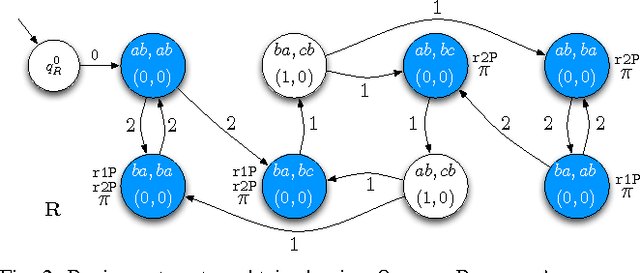
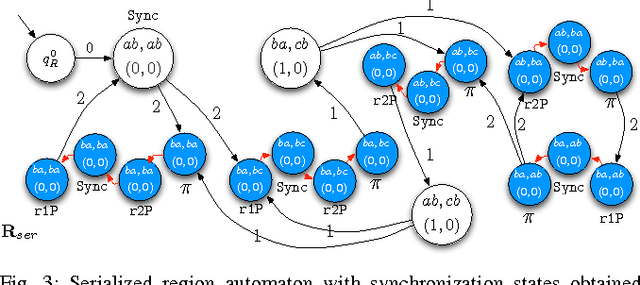
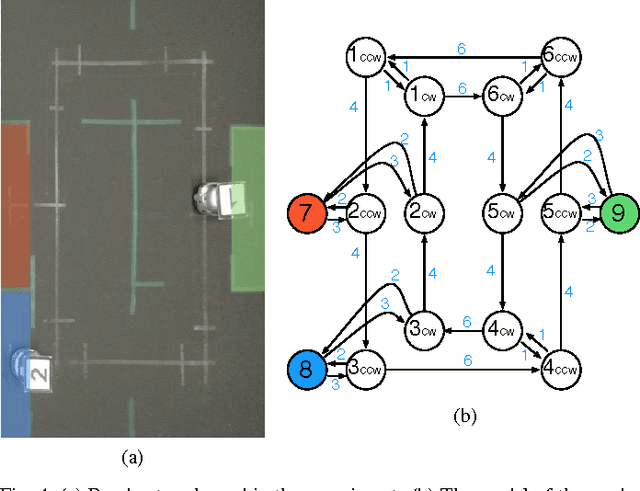
In this paper we present a method for automatically planning robust optimal paths for a group of robots that satisfy a common high level mission specification. Each robot's motion in the environment is modeled as a weighted transition system, and the mission is given as a Linear Temporal Logic (LTL) formula over a set of propositions satisfied by the regions of the environment. In addition, an optimizing proposition must repeatedly be satisfied. The goal is to minimize the maximum time between satisfying instances of the optimizing proposition while ensuring that the LTL formula is satisfied even with uncertainty in the robots' traveling times. We characterize a class of LTL formulas that are robust to robot timing errors, for which we generate optimal paths if no timing errors are present, and we present bounds on the deviation from the optimal values in the presence of errors. We implement and experimentally evaluate our method considering a persistent monitoring task in a road network environment.

Incremental Temporal Logic Synthesis of Control Policies for Robots Interacting with Dynamic Agents

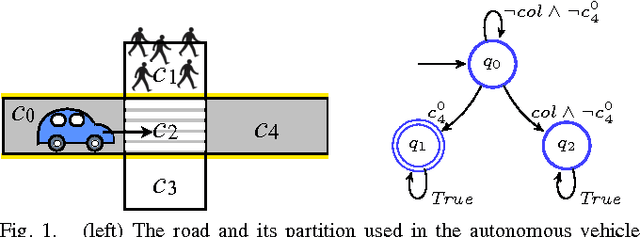
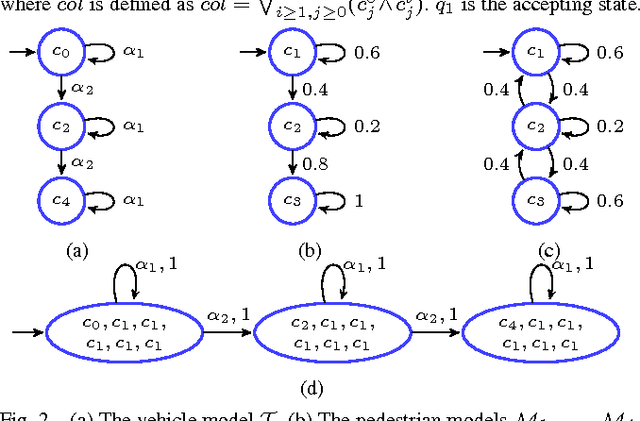
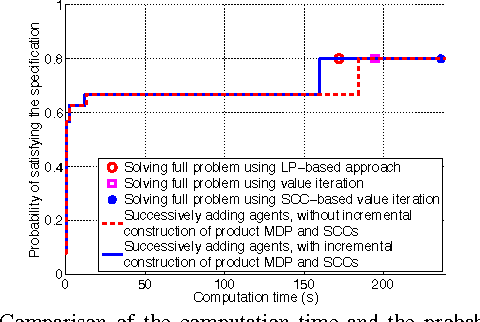
We consider the synthesis of control policies from temporal logic specifications for robots that interact with multiple dynamic environment agents. Each environment agent is modeled by a Markov chain whereas the robot is modeled by a finite transition system (in the deterministic case) or Markov decision process (in the stochastic case). Existing results in probabilistic verification are adapted to solve the synthesis problem. To partially address the state explosion issue, we propose an incremental approach where only a small subset of environment agents is incorporated in the synthesis procedure initially and more agents are successively added until we hit the constraints on computational resources. Our algorithm runs in an anytime fashion where the probability that the robot satisfies its specification increases as the algorithm progresses.

Optimal Multi-Robot Path Planning with Temporal Logic Constraints

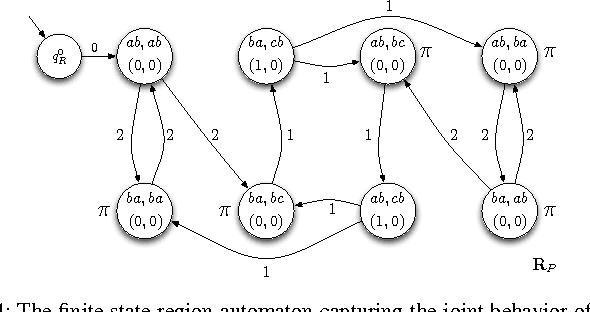
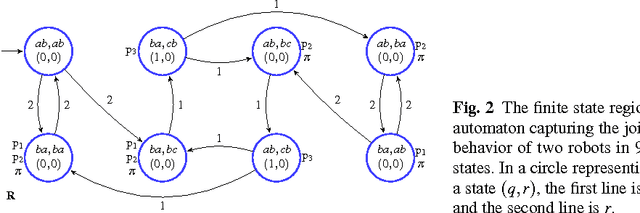
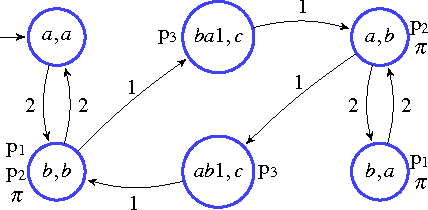
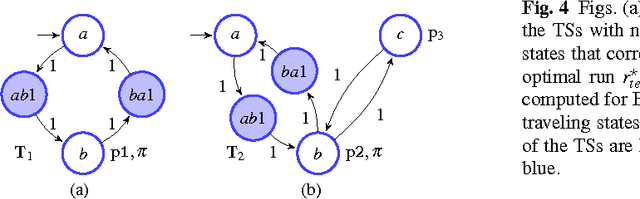
In this paper we present a method for automatically planning optimal paths for a group of robots that satisfy a common high level mission specification. Each robot's motion in the environment is modeled as a weighted transition system. The mission is given as a Linear Temporal Logic formula. In addition, an optimizing proposition must repeatedly be satisfied. The goal is to minimize the maximum time between satisfying instances of the optimizing proposition. Our method is guaranteed to compute an optimal set of robot paths. We utilize a timed automaton representation in order to capture the relative position of the robots in the environment. We then obtain a bisimulation of this timed automaton as a finite transition system that captures the joint behavior of the robots and apply our earlier algorithm for the single robot case to optimize the group motion. We present a simulation of a persistent monitoring task in a road network environment.