LTL Control in Uncertain Environments with Probabilistic Satisfaction Guarantees
Paper and Code
Apr 07, 2011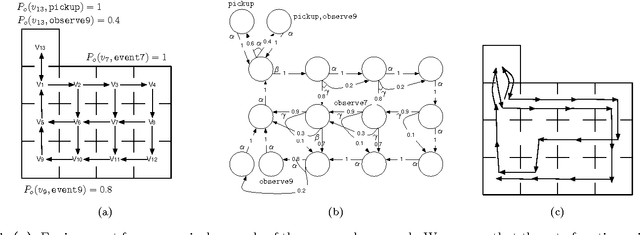
We present a method to generate a robot control strategy that maximizes the probability to accomplish a task. The task is given as a Linear Temporal Logic (LTL) formula over a set of properties that can be satisfied at the regions of a partitioned environment. We assume that the probabilities with which the properties are satisfied at the regions are known, and the robot can determine the truth value of a proposition only at the current region. Motivated by several results on partitioned-based abstractions, we assume that the motion is performed on a graph. To account for noisy sensors and actuators, we assume that a control action enables several transitions with known probabilities. We show that this problem can be reduced to the problem of generating a control policy for a Markov Decision Process (MDP) such that the probability of satisfying an LTL formula over its states is maximized. We provide a complete solution for the latter problem that builds on existing results from probabilistic model checking. We include an illustrative case study.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge