ColorVein: Colorful Cancelable Vein Biometrics

Vein recognition technologies have become one of the primary solutions for high-security identification systems. However, the issue of biometric information leakage can still pose a serious threat to user privacy and anonymity. Currently, there is no cancelable biometric template generation scheme specifically designed for vein biometrics. Therefore, this paper proposes an innovative cancelable vein biometric generation scheme: ColorVein. Unlike previous cancelable template generation schemes, ColorVein does not destroy the original biometric features and introduces additional color information to grayscale vein images. This method significantly enhances the information density of vein images by transforming static grayscale information into dynamically controllable color representations through interactive colorization. ColorVein allows users/administrators to define a controllable pseudo-random color space for grayscale vein images by editing the position, number, and color of hint points, thereby generating protected cancelable templates. Additionally, we propose a new secure center loss to optimize the training process of the protected feature extraction model, effectively increasing the feature distance between enrolled users and any potential impostors. Finally, we evaluate ColorVein's performance on all types of vein biometrics, including recognition performance, unlinkability, irreversibility, and revocability, and conduct security and privacy analyses. ColorVein achieves competitive performance compared with state-of-the-art methods.

Decentralized Nonconvex Composite Federated Learning with Gradient Tracking and Momentum

Decentralized Federated Learning (DFL) eliminates the reliance on the server-client architecture inherent in traditional federated learning, attracting significant research interest in recent years. Simultaneously, the objective functions in machine learning tasks are often nonconvex and frequently incorporate additional, potentially nonsmooth regularization terms to satisfy practical requirements, thereby forming nonconvex composite optimization problems. Employing DFL methods to solve such general optimization problems leads to the formulation of Decentralized Nonconvex Composite Federated Learning (DNCFL), a topic that remains largely underexplored. In this paper, we propose a novel DNCFL algorithm, termed \bf{DEPOSITUM}. Built upon proximal stochastic gradient tracking, DEPOSITUM mitigates the impact of data heterogeneity by enabling clients to approximate the global gradient. The introduction of momentums in the proximal gradient descent step, replacing tracking variables, reduces the variance introduced by stochastic gradients. Additionally, DEPOSITUM supports local updates of client variables, significantly reducing communication costs. Theoretical analysis demonstrates that DEPOSITUM achieves an expected $\epsilon$-stationary point with an iteration complexity of $\mathcal{O}(1/\epsilon^2)$. The proximal gradient, consensus errors, and gradient estimation errors decrease at a sublinear rate of $\mathcal{O}(1/T)$. With appropriate parameter selection, the algorithm achieves network-independent linear speedup without requiring mega-batch sampling. Finally, we apply DEPOSITUM to the training of neural networks on real-world datasets, systematically examining the influence of various hyperparameters on its performance. Comparisons with other federated composite optimization algorithms validate the effectiveness of the proposed method.

FedCanon: Non-Convex Composite Federated Learning with Efficient Proximal Operation on Heterogeneous Data

Composite federated learning offers a general framework for solving machine learning problems with additional regularization terms. However, many existing methods require clients to perform multiple proximal operations to handle non-smooth terms and their performance are often susceptible to data heterogeneity. To overcome these limitations, we propose a novel composite federated learning algorithm called \textbf{FedCanon}, designed to solve the optimization problems comprising a possibly non-convex loss function and a weakly convex, potentially non-smooth regularization term. By decoupling proximal mappings from local updates, FedCanon requires only a single proximal evaluation on the server per iteration, thereby reducing the overall proximal computation cost. It also introduces control variables that incorporate global gradient information into client updates, which helps mitigate the effects of data heterogeneity. Theoretical analysis demonstrates that FedCanon achieves sublinear convergence rates under general non-convex settings and linear convergence under the Polyak-{\L}ojasiewicz condition, without relying on bounded heterogeneity assumptions. Experiments demonstrate that FedCanon outperforms the state-of-the-art methods in terms of both accuracy and computational efficiency, particularly under heterogeneous data distributions.

Improving Fast Adversarial Training via Self-Knowledge Guidance

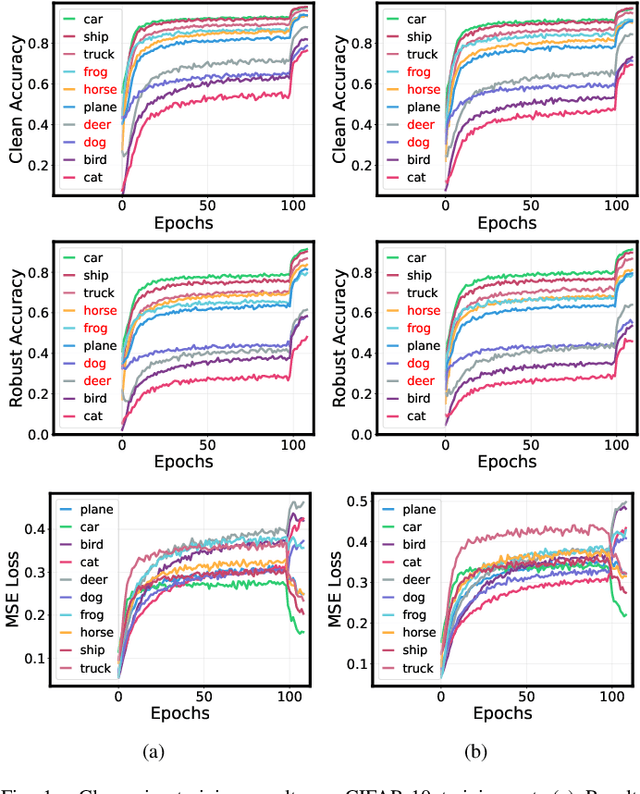
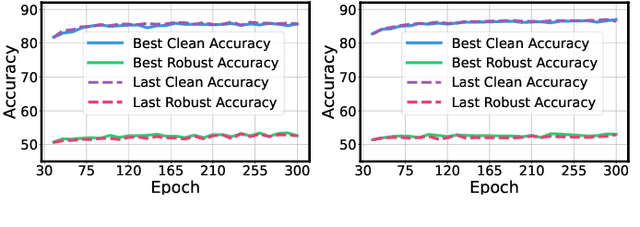
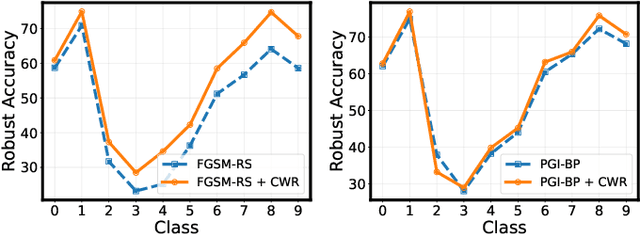
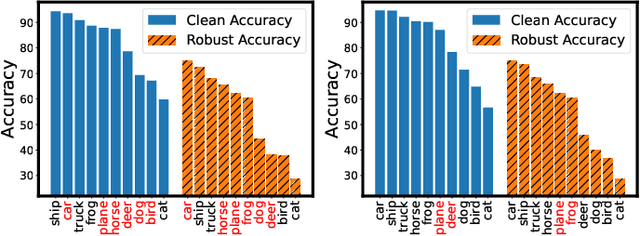
Adversarial training has achieved remarkable advancements in defending against adversarial attacks. Among them, fast adversarial training (FAT) is gaining attention for its ability to achieve competitive robustness with fewer computing resources. Existing FAT methods typically employ a uniform strategy that optimizes all training data equally without considering the influence of different examples, which leads to an imbalanced optimization. However, this imbalance remains unexplored in the field of FAT. In this paper, we conduct a comprehensive study of the imbalance issue in FAT and observe an obvious class disparity regarding their performances. This disparity could be embodied from a perspective of alignment between clean and robust accuracy. Based on the analysis, we mainly attribute the observed misalignment and disparity to the imbalanced optimization in FAT, which motivates us to optimize different training data adaptively to enhance robustness. Specifically, we take disparity and misalignment into consideration. First, we introduce self-knowledge guided regularization, which assigns differentiated regularization weights to each class based on its training state, alleviating class disparity. Additionally, we propose self-knowledge guided label relaxation, which adjusts label relaxation according to the training accuracy, alleviating the misalignment and improving robustness. By combining these methods, we formulate the Self-Knowledge Guided FAT (SKG-FAT), leveraging naturally generated knowledge during training to enhance the adversarial robustness without compromising training efficiency. Extensive experiments on four standard datasets demonstrate that the SKG-FAT improves the robustness and preserves competitive clean accuracy, outperforming the state-of-the-art methods.

MG-Skip: Random Multi-Gossip Skipping Method for Nonsmooth Distributed Optimization

Distributed optimization methods with probabilistic local updates have recently gained attention for their provable ability to communication acceleration. Nevertheless, this capability is effective only when the loss function is smooth and the network is sufficiently well-connected. In this paper, we propose the first linear convergent method MG-Skip with probabilistic local updates for nonsmooth distributed optimization. Without any extra condition for the network connectivity, MG-Skip allows for the multiple-round gossip communication to be skipped in most iterations, while its iteration complexity is $\mathcal{O}\left(\kappa \log \frac{1}{\epsilon}\right)$ and communication complexity is only $\mathcal{O}\left(\sqrt{\frac{\kappa}{(1-\rho)}} \log \frac{1}{\epsilon}\right)$, where $\kappa$ is the condition number of the loss function and $\rho$ reflects the connectivity of the network topology. To the best of our knowledge, MG-Skip achieves the best communication complexity when the loss function has the smooth (strongly convex)+nonsmooth (convex) composite form.

A data-driven rutting depth short-time prediction model with metaheuristic optimization for asphalt pavements based on RIOHTrack

Rutting of asphalt pavements is a crucial design criterion in various pavement design guides. A good road transportation base can provide security for the transportation of oil and gas in road transportation. This study attempts to develop a robust artificial intelligence model to estimate different asphalt pavements' rutting depth clips, temperature, and load axes as primary characteristics. The experiment data were obtained from 19 asphalt pavements with different crude oil sources on a 2.038 km long full-scale field accelerated pavement test track (RIOHTrack, Road Track Institute) in Tongzhou, Beijing. In addition, this paper also proposes to build complex networks with different pavement rutting depths through complex network methods and the Louvain algorithm for community detection. The most critical structural elements can be selected from different asphalt pavement rutting data, and similar structural elements can be found. An extreme learning machine algorithm with residual correction (RELM) is designed and optimized using an independent adaptive particle swarm algorithm. The experimental results of the proposed method are compared with several classical machine learning algorithms, with predictions of Average Root Mean Squared Error, Average Mean Absolute Error, and Average Mean Absolute Percentage Error for 19 asphalt pavements reaching 1.742, 1.363, and 1.94\% respectively. The experiments demonstrate that the RELM algorithm has an advantage over classical machine learning methods in dealing with non-linear problems in road engineering. Notably, the method ensures the adaptation of the simulated environment to different levels of abstraction through the cognitive analysis of the production environment parameters.

Decentralized Inexact Proximal Gradient Method With Network-Independent Stepsizes for Convex Composite Optimization

This paper considers decentralized convex composite optimization over undirected and connected networks, where the local loss function contains both smooth and nonsmooth terms. For this problem, a novel CTA (Combine-Then-Adapt)-based decentralized algorithm is proposed under uncoordinated network-independent constant stepsizes. Particularly, the proposed algorithm only needs to approximately solve a sequence of proximal mappings, which benefits the decentralized composite optimization where the proximal mappings of the nonsmooth loss functions may not have analytic solutions. For the general convex case, we prove the O(1/k) convergence rate of the proposed algorithm, which can be improved to o(1/k) if the proximal mappings are solved exactly. Moreover, with metric subregularity, we establish the linear convergence rate. Finally, the numerical experiments demonstrate the efficiency of the algorithm.

BALPA: A Balanced Primal-Dual Algorithm for Nonsmooth Optimization with Application to Distributed Optimization

In this paper, we propose a novel primal-dual proximal splitting algorithm (PD-PSA), named BALPA, for the composite optimization problem with equality constraints, where the loss function consists of a smooth term and a nonsmooth term composed with a linear mapping. In BALPA, the dual update is designed as a proximal point for a time-varying quadratic function, which balances the implementation of primal and dual update and retains the proximity-induced feature of classic PD-PSAs. In addition, by this balance, BALPA eliminates the inefficiency of classic PD-PSAs for composite optimization problems in which the Euclidean norm of the linear mapping or the equality constraint mapping is large. Therefore, BALPA not only inherits the advantages of simple structure and easy implementation of classic PD-PSAs but also ensures a fast convergence when these norms are large. Moreover, we propose a stochastic version of BALPA (S-BALPA) and apply the developed BALPA to distributed optimization to devise a new distributed optimization algorithm. Furthermore, a comprehensive convergence analysis for BALPA and S-BALPA is conducted, respectively. Finally, numerical experiments demonstrate the efficiency of the proposed algorithms.

DISA: A Dual Inexact Splitting Algorithm for Distributed Convex Composite Optimization

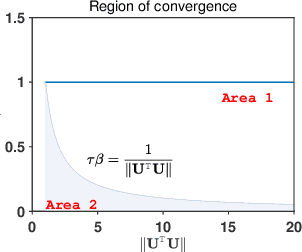
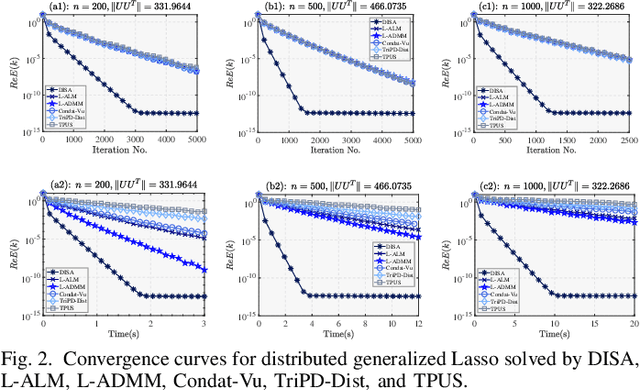
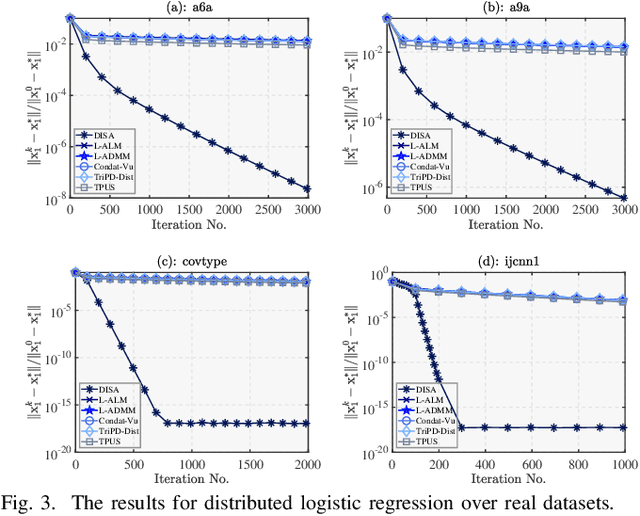
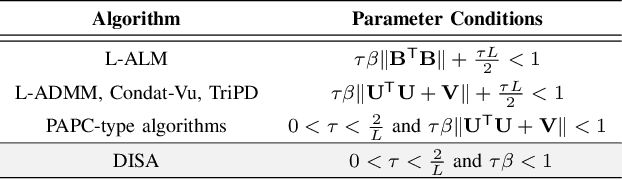
This paper proposes a novel dual inexact splitting algorithm (DISA) for the distributed convex composite optimization problem, where the local loss function consists of an $L$-smooth term and a possibly nonsmooth term which is composed with a linear operator. We prove that DISA is convergent when the primal and dual stepsizes $\tau$, $\beta$ satisfy $0<\tau<{2}/{L}$ and $0<\tau\beta <1$. Compared with existing primal-dual proximal splitting algorithms (PD-PSAs), DISA overcomes the dependence of the convergence stepsize range on the Euclidean norm of the linear operator. It implies that DISA allows for larger stepsizes when the Euclidean norm is large, thus ensuring fast convergence of it. Moreover, we establish the sublinear and linear convergence rate of DISA under general convexity and metric subregularity, respectively. Furthermore, an approximate iterative version of DISA is provided, and the global convergence and sublinear convergence rate of this approximate version are proved. Finally, numerical experiments not only corroborate the theoretical analyses but also indicate that DISA achieves a significant acceleration compared with the existing PD-PSAs.