MG-Skip: Random Multi-Gossip Skipping Method for Nonsmooth Distributed Optimization

Distributed optimization methods with probabilistic local updates have recently gained attention for their provable ability to communication acceleration. Nevertheless, this capability is effective only when the loss function is smooth and the network is sufficiently well-connected. In this paper, we propose the first linear convergent method MG-Skip with probabilistic local updates for nonsmooth distributed optimization. Without any extra condition for the network connectivity, MG-Skip allows for the multiple-round gossip communication to be skipped in most iterations, while its iteration complexity is $\mathcal{O}\left(\kappa \log \frac{1}{\epsilon}\right)$ and communication complexity is only $\mathcal{O}\left(\sqrt{\frac{\kappa}{(1-\rho)}} \log \frac{1}{\epsilon}\right)$, where $\kappa$ is the condition number of the loss function and $\rho$ reflects the connectivity of the network topology. To the best of our knowledge, MG-Skip achieves the best communication complexity when the loss function has the smooth (strongly convex)+nonsmooth (convex) composite form.

RandCom: Random Communication Skipping Method for Decentralized Stochastic Optimization

Distributed optimization methods with random communication skips are gaining increasing attention due to their proven benefits in accelerating communication complexity. Nevertheless, existing research mainly focuses on centralized communication protocols for strongly convex deterministic settings. In this work, we provide a decentralized optimization method called RandCom, which incorporates probabilistic local updates. We analyze the performance of RandCom in stochastic non-convex, convex, and strongly convex settings and demonstrate its ability to asymptotically reduce communication overhead by the probability of communication. Additionally, we prove that RandCom achieves linear speedup as the number of nodes increases. In stochastic strongly convex settings, we further prove that RandCom can achieve linear speedup with network-independent stepsizes. Moreover, we apply RandCom to federated learning and provide positive results concerning the potential for achieving linear speedup and the suitability of the probabilistic local update approach for non-convex settings.

Decentralized Inexact Proximal Gradient Method With Network-Independent Stepsizes for Convex Composite Optimization

This paper considers decentralized convex composite optimization over undirected and connected networks, where the local loss function contains both smooth and nonsmooth terms. For this problem, a novel CTA (Combine-Then-Adapt)-based decentralized algorithm is proposed under uncoordinated network-independent constant stepsizes. Particularly, the proposed algorithm only needs to approximately solve a sequence of proximal mappings, which benefits the decentralized composite optimization where the proximal mappings of the nonsmooth loss functions may not have analytic solutions. For the general convex case, we prove the O(1/k) convergence rate of the proposed algorithm, which can be improved to o(1/k) if the proximal mappings are solved exactly. Moreover, with metric subregularity, we establish the linear convergence rate. Finally, the numerical experiments demonstrate the efficiency of the algorithm.

BALPA: A Balanced Primal-Dual Algorithm for Nonsmooth Optimization with Application to Distributed Optimization

In this paper, we propose a novel primal-dual proximal splitting algorithm (PD-PSA), named BALPA, for the composite optimization problem with equality constraints, where the loss function consists of a smooth term and a nonsmooth term composed with a linear mapping. In BALPA, the dual update is designed as a proximal point for a time-varying quadratic function, which balances the implementation of primal and dual update and retains the proximity-induced feature of classic PD-PSAs. In addition, by this balance, BALPA eliminates the inefficiency of classic PD-PSAs for composite optimization problems in which the Euclidean norm of the linear mapping or the equality constraint mapping is large. Therefore, BALPA not only inherits the advantages of simple structure and easy implementation of classic PD-PSAs but also ensures a fast convergence when these norms are large. Moreover, we propose a stochastic version of BALPA (S-BALPA) and apply the developed BALPA to distributed optimization to devise a new distributed optimization algorithm. Furthermore, a comprehensive convergence analysis for BALPA and S-BALPA is conducted, respectively. Finally, numerical experiments demonstrate the efficiency of the proposed algorithms.

DISA: A Dual Inexact Splitting Algorithm for Distributed Convex Composite Optimization

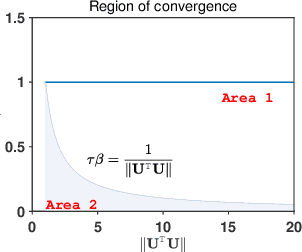
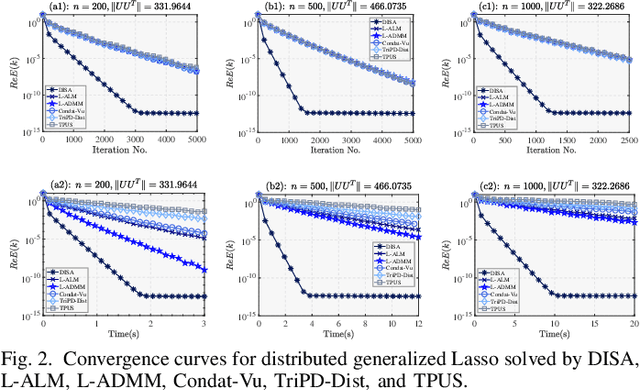
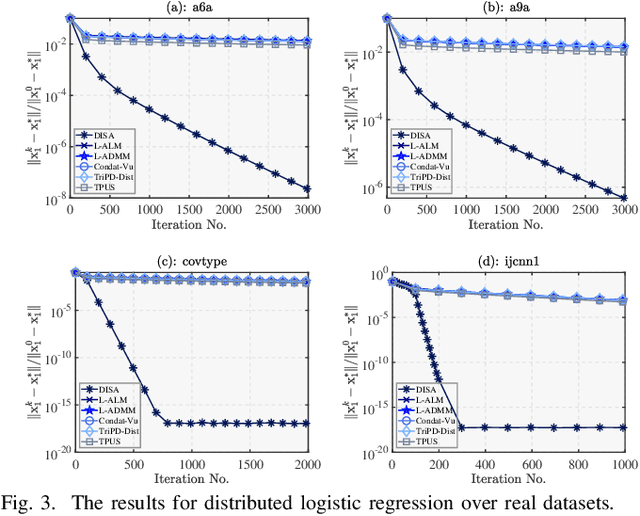
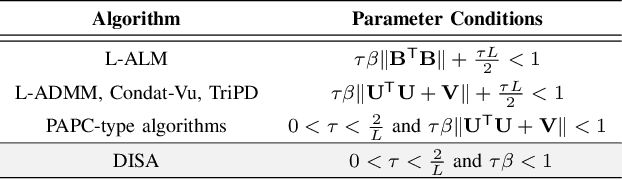
This paper proposes a novel dual inexact splitting algorithm (DISA) for the distributed convex composite optimization problem, where the local loss function consists of an $L$-smooth term and a possibly nonsmooth term which is composed with a linear operator. We prove that DISA is convergent when the primal and dual stepsizes $\tau$, $\beta$ satisfy $0<\tau<{2}/{L}$ and $0<\tau\beta <1$. Compared with existing primal-dual proximal splitting algorithms (PD-PSAs), DISA overcomes the dependence of the convergence stepsize range on the Euclidean norm of the linear operator. It implies that DISA allows for larger stepsizes when the Euclidean norm is large, thus ensuring fast convergence of it. Moreover, we establish the sublinear and linear convergence rate of DISA under general convexity and metric subregularity, respectively. Furthermore, an approximate iterative version of DISA is provided, and the global convergence and sublinear convergence rate of this approximate version are proved. Finally, numerical experiments not only corroborate the theoretical analyses but also indicate that DISA achieves a significant acceleration compared with the existing PD-PSAs.