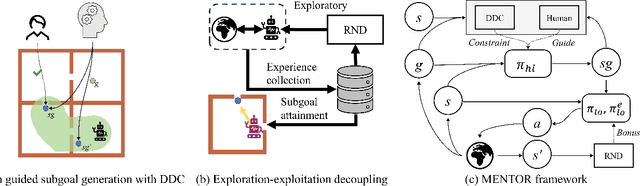
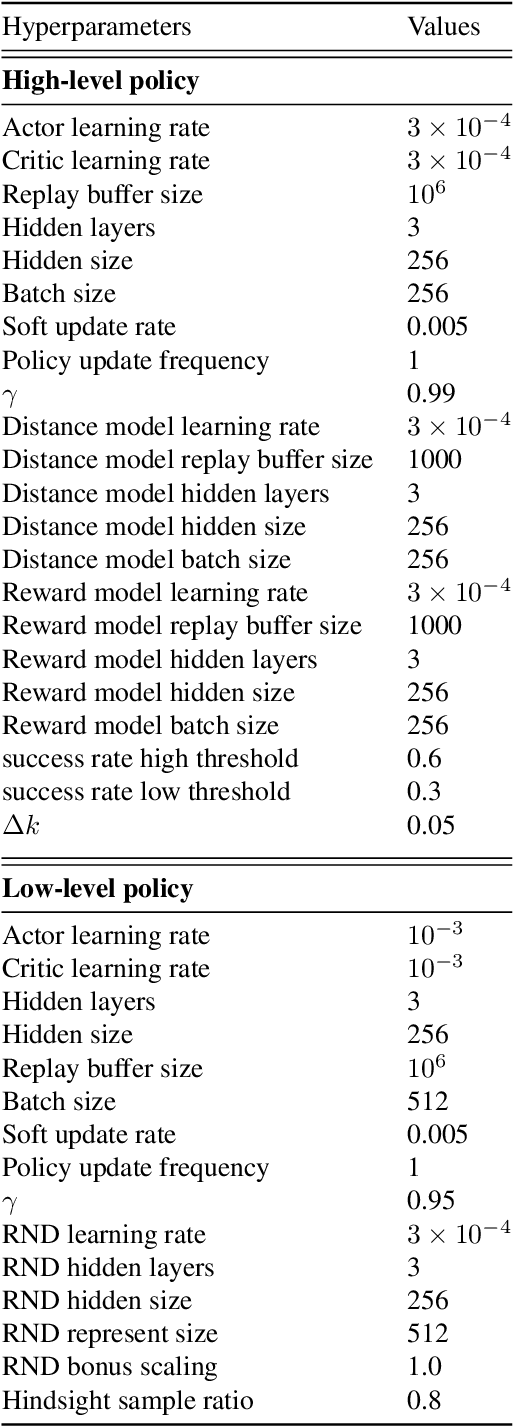
MENTOR: Guiding Hierarchical Reinforcement Learning with Human Feedback and Dynamic Distance Constraint

Hierarchical reinforcement learning (HRL) provides a promising solution for complex tasks with sparse rewards of intelligent agents, which uses a hierarchical framework that divides tasks into subgoals and completes them sequentially. However, current methods struggle to find suitable subgoals for ensuring a stable learning process. Without additional guidance, it is impractical to rely solely on exploration or heuristics methods to determine subgoals in a large goal space. To address the issue, We propose a general hierarchical reinforcement learning framework incorporating human feedback and dynamic distance constraints (MENTOR). MENTOR acts as a "mentor", incorporating human feedback into high-level policy learning, to find better subgoals. As for low-level policy, MENTOR designs a dual policy for exploration-exploitation decoupling respectively to stabilize the training. Furthermore, although humans can simply break down tasks into subgoals to guide the right learning direction, subgoals that are too difficult or too easy can still hinder downstream learning efficiency. We propose the Dynamic Distance Constraint (DDC) mechanism dynamically adjusting the space of optional subgoals. Thus MENTOR can generate subgoals matching the low-level policy learning process from easy to hard. Extensive experiments demonstrate that MENTOR uses a small amount of human feedback to achieve significant improvement in complex tasks with sparse rewards.

BALPA: A Balanced Primal-Dual Algorithm for Nonsmooth Optimization with Application to Distributed Optimization

In this paper, we propose a novel primal-dual proximal splitting algorithm (PD-PSA), named BALPA, for the composite optimization problem with equality constraints, where the loss function consists of a smooth term and a nonsmooth term composed with a linear mapping. In BALPA, the dual update is designed as a proximal point for a time-varying quadratic function, which balances the implementation of primal and dual update and retains the proximity-induced feature of classic PD-PSAs. In addition, by this balance, BALPA eliminates the inefficiency of classic PD-PSAs for composite optimization problems in which the Euclidean norm of the linear mapping or the equality constraint mapping is large. Therefore, BALPA not only inherits the advantages of simple structure and easy implementation of classic PD-PSAs but also ensures a fast convergence when these norms are large. Moreover, we propose a stochastic version of BALPA (S-BALPA) and apply the developed BALPA to distributed optimization to devise a new distributed optimization algorithm. Furthermore, a comprehensive convergence analysis for BALPA and S-BALPA is conducted, respectively. Finally, numerical experiments demonstrate the efficiency of the proposed algorithms.

DISA: A Dual Inexact Splitting Algorithm for Distributed Convex Composite Optimization

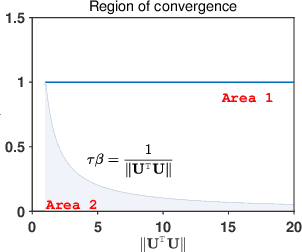
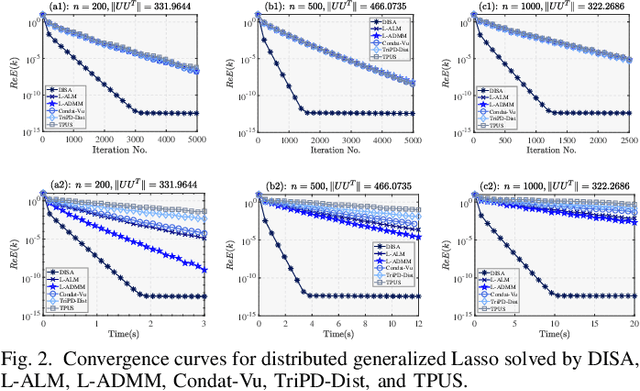
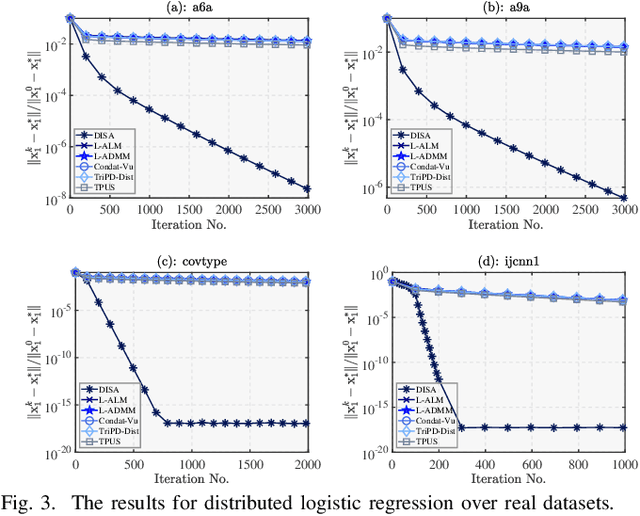
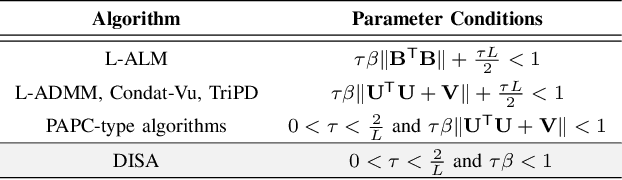
This paper proposes a novel dual inexact splitting algorithm (DISA) for the distributed convex composite optimization problem, where the local loss function consists of an $L$-smooth term and a possibly nonsmooth term which is composed with a linear operator. We prove that DISA is convergent when the primal and dual stepsizes $\tau$, $\beta$ satisfy $0<\tau<{2}/{L}$ and $0<\tau\beta <1$. Compared with existing primal-dual proximal splitting algorithms (PD-PSAs), DISA overcomes the dependence of the convergence stepsize range on the Euclidean norm of the linear operator. It implies that DISA allows for larger stepsizes when the Euclidean norm is large, thus ensuring fast convergence of it. Moreover, we establish the sublinear and linear convergence rate of DISA under general convexity and metric subregularity, respectively. Furthermore, an approximate iterative version of DISA is provided, and the global convergence and sublinear convergence rate of this approximate version are proved. Finally, numerical experiments not only corroborate the theoretical analyses but also indicate that DISA achieves a significant acceleration compared with the existing PD-PSAs.