DISA: A Dual Inexact Splitting Algorithm for Distributed Convex Composite Optimization

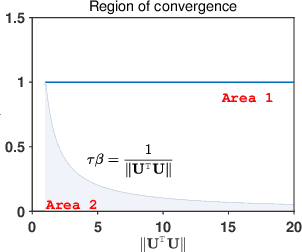
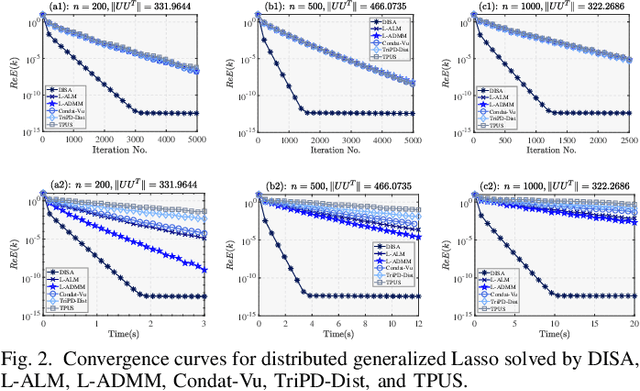
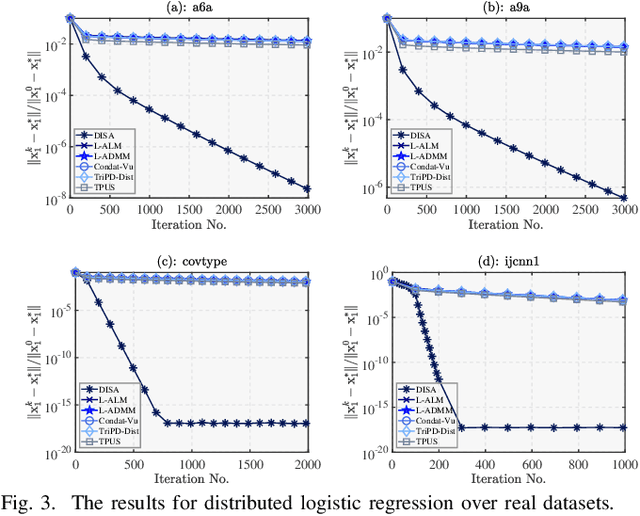
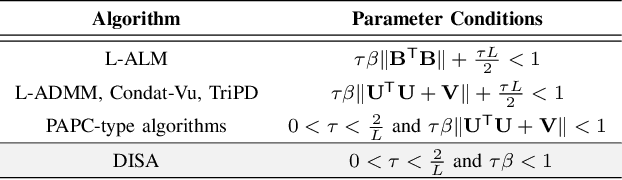
This paper proposes a novel dual inexact splitting algorithm (DISA) for the distributed convex composite optimization problem, where the local loss function consists of an $L$-smooth term and a possibly nonsmooth term which is composed with a linear operator. We prove that DISA is convergent when the primal and dual stepsizes $\tau$, $\beta$ satisfy $0<\tau<{2}/{L}$ and $0<\tau\beta <1$. Compared with existing primal-dual proximal splitting algorithms (PD-PSAs), DISA overcomes the dependence of the convergence stepsize range on the Euclidean norm of the linear operator. It implies that DISA allows for larger stepsizes when the Euclidean norm is large, thus ensuring fast convergence of it. Moreover, we establish the sublinear and linear convergence rate of DISA under general convexity and metric subregularity, respectively. Furthermore, an approximate iterative version of DISA is provided, and the global convergence and sublinear convergence rate of this approximate version are proved. Finally, numerical experiments not only corroborate the theoretical analyses but also indicate that DISA achieves a significant acceleration compared with the existing PD-PSAs.