Xiaohan Yi
PIG-Nav: Key Insights for Pretrained Image Goal Navigation Models
Jul 23, 2025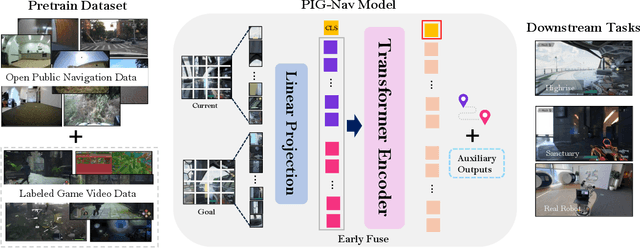
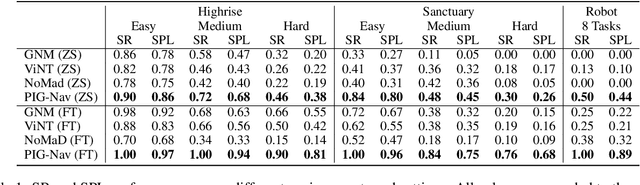
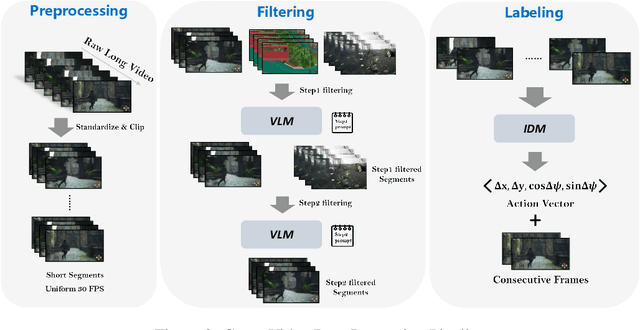
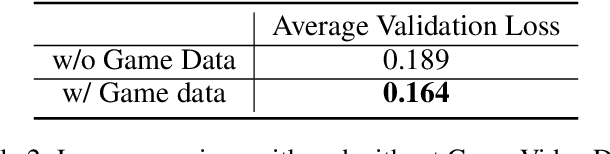
Abstract:Recent studies have explored pretrained (foundation) models for vision-based robotic navigation, aiming to achieve generalizable navigation and positive transfer across diverse environments while enhancing zero-shot performance in unseen settings. In this work, we introduce PIG-Nav (Pretrained Image-Goal Navigation), a new approach that further investigates pretraining strategies for vision-based navigation models and contributes in two key areas. Model-wise, we identify two critical design choices that consistently improve the performance of pretrained navigation models: (1) integrating an early-fusion network structure to combine visual observations and goal images via appropriately pretrained Vision Transformer (ViT) image encoder, and (2) introducing suitable auxiliary tasks to enhance global navigation representation learning, thus further improving navigation performance. Dataset-wise, we propose a novel data preprocessing pipeline for efficiently labeling large-scale game video datasets for navigation model training. We demonstrate that augmenting existing open navigation datasets with diverse gameplay videos improves model performance. Our model achieves an average improvement of 22.6% in zero-shot settings and a 37.5% improvement in fine-tuning settings over existing visual navigation foundation models in two complex simulated environments and one real-world environment. These results advance the state-of-the-art in pretrained image-goal navigation models. Notably, our model maintains competitive performance while requiring significantly less fine-tuning data, highlighting its potential for real-world deployment with minimal labeled supervision.
UniGraspTransformer: Simplified Policy Distillation for Scalable Dexterous Robotic Grasping
Dec 03, 2024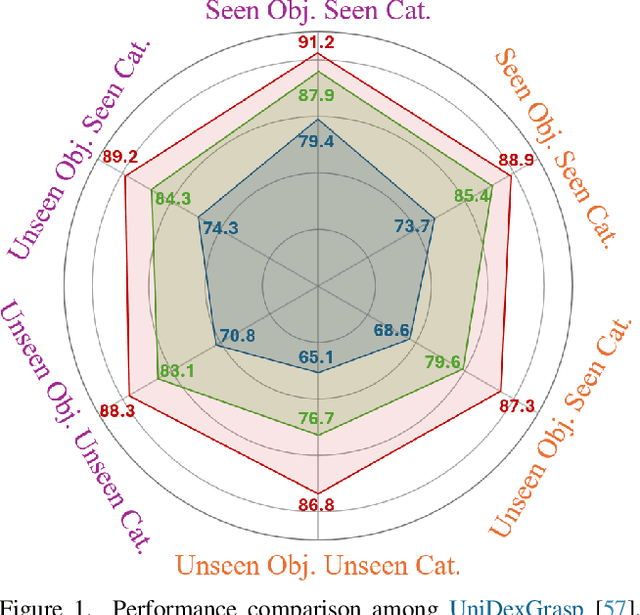

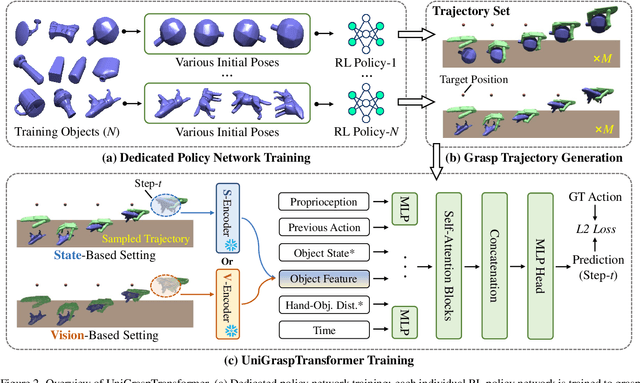

Abstract:We introduce UniGraspTransformer, a universal Transformer-based network for dexterous robotic grasping that simplifies training while enhancing scalability and performance. Unlike prior methods such as UniDexGrasp++, which require complex, multi-step training pipelines, UniGraspTransformer follows a streamlined process: first, dedicated policy networks are trained for individual objects using reinforcement learning to generate successful grasp trajectories; then, these trajectories are distilled into a single, universal network. Our approach enables UniGraspTransformer to scale effectively, incorporating up to 12 self-attention blocks for handling thousands of objects with diverse poses. Additionally, it generalizes well to both idealized and real-world inputs, evaluated in state-based and vision-based settings. Notably, UniGraspTransformer generates a broader range of grasping poses for objects in various shapes and orientations, resulting in more diverse grasp strategies. Experimental results demonstrate significant improvements over state-of-the-art, UniDexGrasp++, across various object categories, achieving success rate gains of 3.5%, 7.7%, and 10.1% on seen objects, unseen objects within seen categories, and completely unseen objects, respectively, in the vision-based setting. Project page: https://dexhand.github.io/UniGraspTransformer.
Less Is More: Fast Multivariate Time Series Forecasting with Light Sampling-oriented MLP Structures
Jul 04, 2022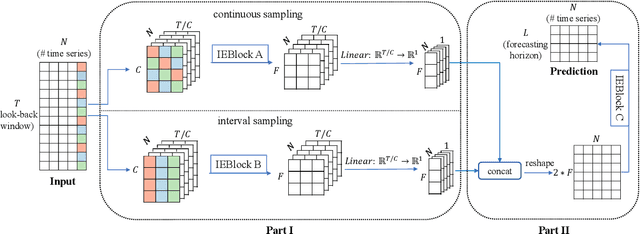
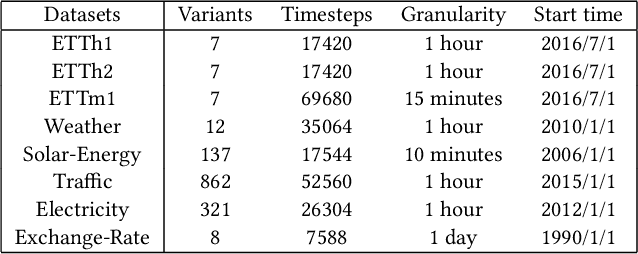
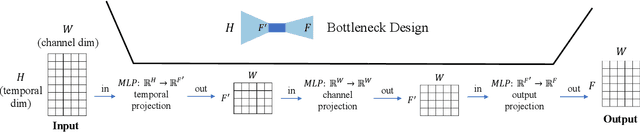
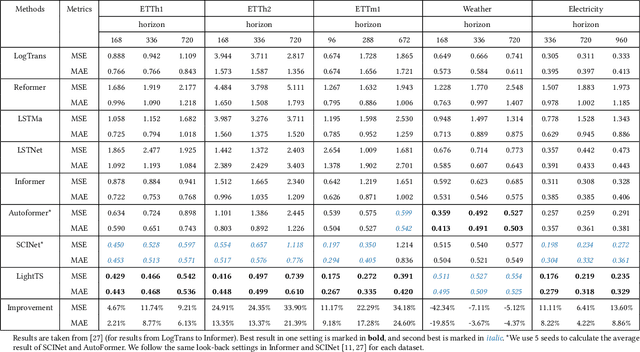
Abstract:Multivariate time series forecasting has seen widely ranging applications in various domains, including finance, traffic, energy, and healthcare. To capture the sophisticated temporal patterns, plenty of research studies designed complex neural network architectures based on many variants of RNNs, GNNs, and Transformers. However, complex models are often computationally expensive and thus face a severe challenge in training and inference efficiency when applied to large-scale real-world datasets. In this paper, we introduce LightTS, a light deep learning architecture merely based on simple MLP-based structures. The key idea of LightTS is to apply an MLP-based structure on top of two delicate down-sampling strategies, including interval sampling and continuous sampling, inspired by a crucial fact that down-sampling time series often preserves the majority of its information. We conduct extensive experiments on eight widely used benchmark datasets. Compared with the existing state-of-the-art methods, LightTS demonstrates better performance on five of them and comparable performance on the rest. Moreover, LightTS is highly efficient. It uses less than 5% FLOPS compared with previous SOTA methods on the largest benchmark dataset. In addition, LightTS is robust and has a much smaller variance in forecasting accuracy than previous SOTA methods in long sequence forecasting tasks.
DEPTS: Deep Expansion Learning for Periodic Time Series Forecasting
Mar 15, 2022
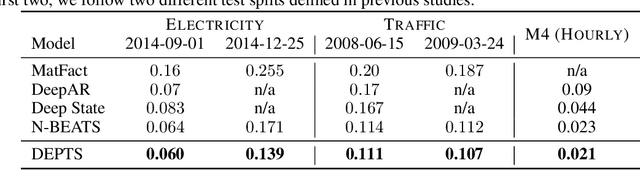
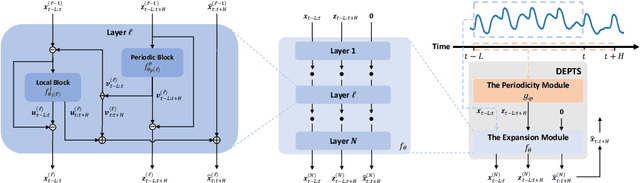
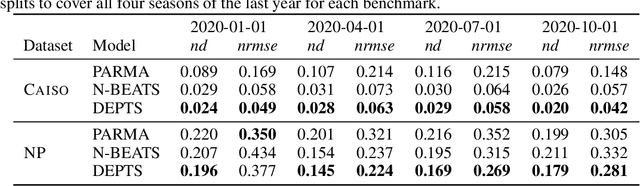
Abstract:Periodic time series (PTS) forecasting plays a crucial role in a variety of industries to foster critical tasks, such as early warning, pre-planning, resource scheduling, etc. However, the complicated dependencies of the PTS signal on its inherent periodicity as well as the sophisticated composition of various periods hinder the performance of PTS forecasting. In this paper, we introduce a deep expansion learning framework, DEPTS, for PTS forecasting. DEPTS starts with a decoupled formulation by introducing the periodic state as a hidden variable, which stimulates us to make two dedicated modules to tackle the aforementioned two challenges. First, we develop an expansion module on top of residual learning to perform a layer-by-layer expansion of those complicated dependencies. Second, we introduce a periodicity module with a parameterized periodic function that holds sufficient capacity to capture diversified periods. Moreover, our two customized modules also have certain interpretable capabilities, such as attributing the forecasts to either local momenta or global periodicity and characterizing certain core periodic properties, e.g., amplitudes and frequencies. Extensive experiments on both synthetic data and real-world data demonstrate the effectiveness of DEPTS on handling PTS. In most cases, DEPTS achieves significant improvements over the best baseline. Specifically, the error reduction can even reach up to 20% for a few cases. Finally, all codes are publicly available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge