An Adaptive Second-order Method for a Class of Nonconvex Nonsmooth Composite Optimization

This paper explores a specific type of nonconvex sparsity-promoting regularization problems, namely those involving $\ell_p$-norm regularization, in conjunction with a twice continuously differentiable loss function. We propose a novel second-order algorithm designed to effectively address this class of challenging nonconvex and nonsmooth problems, showcasing several innovative features: (i) The use of an alternating strategy to solve a reweighted $\ell_1$ regularized subproblem and the subspace approximate Newton step. (ii) The reweighted $\ell_1$ regularized subproblem relies on a convex approximation to the nonconvex regularization term, enabling a closed-form solution characterized by the soft-thresholding operator. This feature allows our method to be applied to various nonconvex regularization problems. (iii) Our algorithm ensures that the iterates maintain their sign values and that nonzero components are kept away from 0 for a sufficient number of iterations, eventually transitioning to a perturbed Newton method. (iv) We provide theoretical guarantees of global convergence, local superlinear convergence in the presence of the Kurdyka-\L ojasiewicz (KL) property, and local quadratic convergence when employing the exact Newton step in our algorithm. We also showcase the effectiveness of our approach through experiments on a diverse set of model prediction problems.

System Report for CCL24-Eval Task 7: Multi-Error Modeling and Fluency-Targeted Pre-training for Chinese Essay Evaluation

This system report presents our approaches and results for the Chinese Essay Fluency Evaluation (CEFE) task at CCL-2024. For Track 1, we optimized predictions for challenging fine-grained error types using binary classification models and trained coarse-grained models on the Chinese Learner 4W corpus. In Track 2, we enhanced performance by constructing a pseudo-dataset with multiple error types per sentence. For Track 3, where we achieved first place, we generated fluency-rated pseudo-data via back-translation for pre-training and used an NSP-based strategy with Symmetric Cross Entropy loss to capture context and mitigate long dependencies. Our methods effectively address key challenges in Chinese Essay Fluency Evaluation.

Efficient Low-rank Identification via Accelerated Iteratively Reweighted Nuclear Norm Minimization

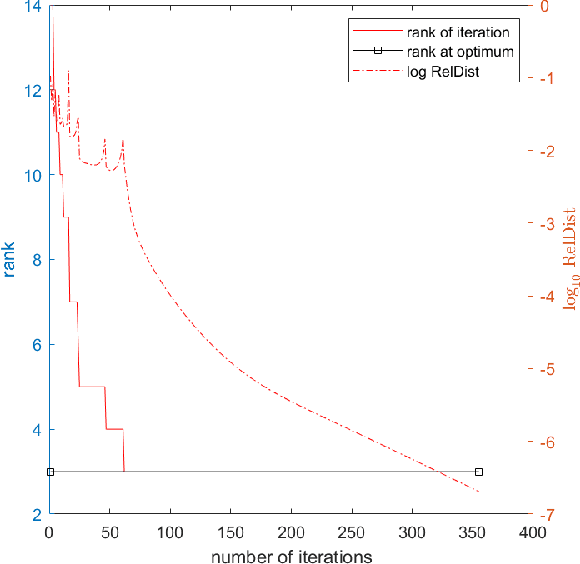
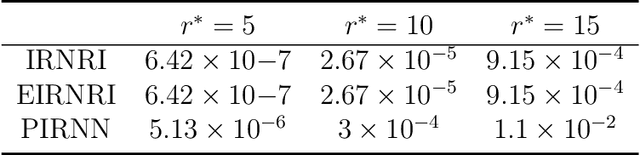
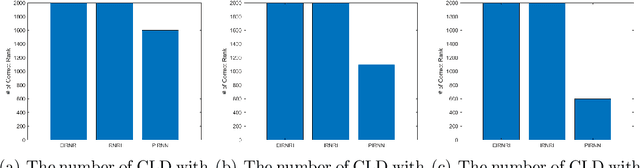
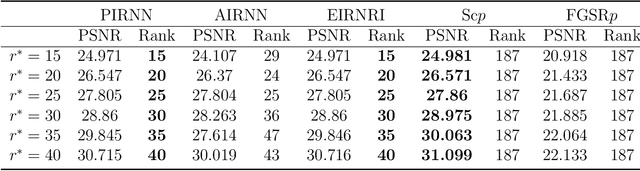
This paper considers the problem of minimizing the sum of a smooth function and the Schatten-$p$ norm of the matrix. Our contribution involves proposing accelerated iteratively reweighted nuclear norm methods designed for solving the nonconvex low-rank minimization problem. Two major novelties characterize our approach. Firstly, the proposed method possesses a rank identification property, enabling the provable identification of the "correct" rank of the stationary point within a finite number of iterations. Secondly, we introduce an adaptive updating strategy for smoothing parameters. This strategy automatically fixes parameters associated with zero singular values as constants upon detecting the "correct" rank while quickly driving the rest of the parameters to zero. This adaptive behavior transforms the algorithm into one that effectively solves smooth problems after a few iterations, setting our work apart from existing iteratively reweighted methods for low-rank optimization. We prove the global convergence of the proposed algorithm, guaranteeing that every limit point of the iterates is a critical point. Furthermore, a local convergence rate analysis is provided under the Kurdyka-{\L}ojasiewicz property. We conduct numerical experiments using both synthetic and real data to showcase our algorithm's efficiency and superiority over existing methods.

A Screening Strategy for Structured Optimization Involving Nonconvex $\ell_{q,p}$ Regularization

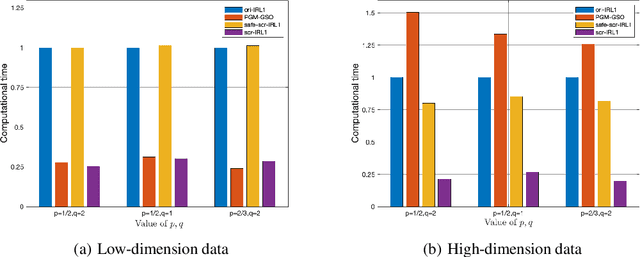
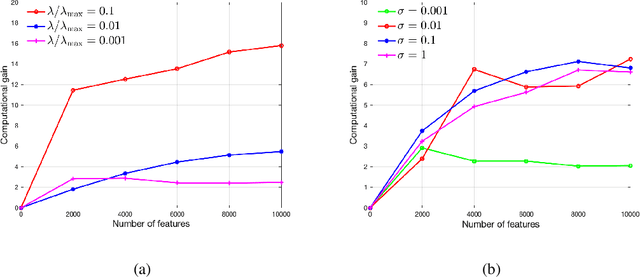
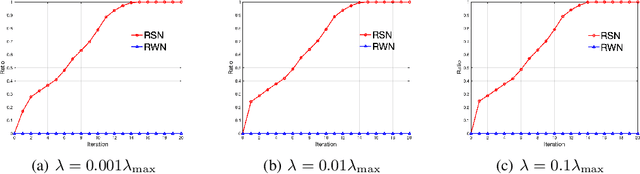
In this paper, we develop a simple yet effective screening rule strategy to improve the computational efficiency in solving structured optimization involving nonconvex $\ell_{q,p}$ regularization. Based on an iteratively reweighted $\ell_1$ (IRL1) framework, the proposed screening rule works like a preprocessing module that potentially removes the inactive groups before starting the subproblem solver, thereby reducing the computational time in total. This is mainly achieved by heuristically exploiting the dual subproblem information during each iteration.Moreover, we prove that our screening rule can remove all inactive variables in a finite number of iterations of the IRL1 method. Numerical experiments illustrate the efficiency of our screening rule strategy compared with several state-of-the-art algorithms.

Traffic Event Detection as a Slot Filling Problem

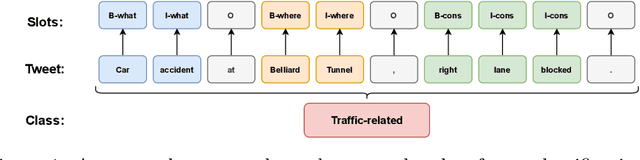
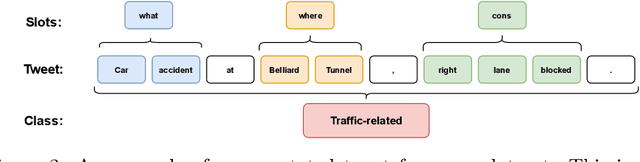
In this paper, we introduce the new problem of extracting fine-grained traffic information from Twitter streams by also making publicly available the two (constructed) traffic-related datasets from Belgium and the Brussels capital region. In particular, we experiment with several models to identify (i) whether a tweet is traffic-related or not, and (ii) in the case that the tweet is traffic-related to identify more fine-grained information regarding the event (e.g., the type of the event, where the event happened). To do so, we frame (i) the problem of identifying whether a tweet is a traffic-related event or not as a text classification subtask, and (ii) the problem of identifying more fine-grained traffic-related information as a slot filling subtask, where fine-grained information (e.g., where an event has happened) is represented as a slot/entity of a particular type. We propose the use of several methods that process the two subtasks either separately or in a joint setting, and we evaluate the effectiveness of the proposed methods for solving the traffic event detection problem. Experimental results indicate that the proposed architectures achieve high performance scores (i.e., more than 95% in terms of F$_{1}$ score) on the constructed datasets for both of the subtasks (i.e., text classification and slot filling) even in a transfer learning scenario. In addition, by incorporating tweet-level information in each of the tokens comprising the tweet (for the BERT-based model) can lead to a performance improvement for the joint setting.

An Iteratively Reweighted Method for Sparse Optimization on Nonconvex $\ell_{p}$ Ball

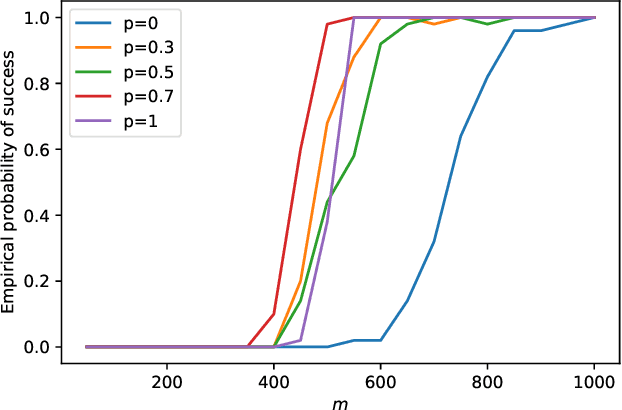
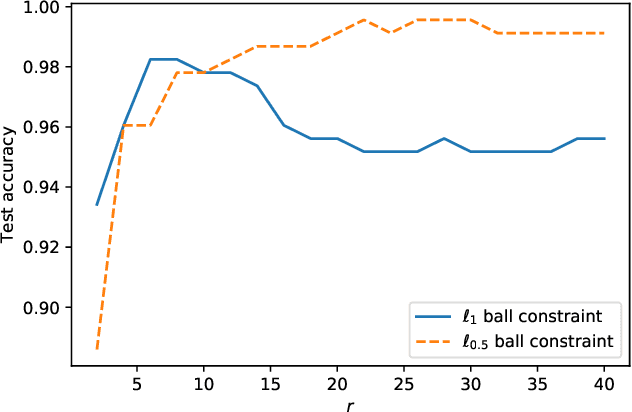
This paper is intended to solve the nonconvex $\ell_{p}$-ball constrained nonlinear optimization problems. An iteratively reweighted method is proposed, which solves a sequence of weighted $\ell_{1}$-ball projection subproblems. At each iteration, the next iterate is obtained by moving along the negative gradient with a stepsize and then projecting the resulted point onto the weighted $\ell_{1}$ ball to approximate the $\ell_{p}$ ball. Specifically, if the current iterate is in the interior of the feasible set, then the weighted $\ell_{1}$ ball is formed by linearizing the $\ell_{p}$ norm at the current iterate. If the current iterate is on the boundary of the feasible set, then the weighted $\ell_{1}$ ball is formed differently by keeping those zero components in the current iterate still zero. In our analysis, we prove that the generated iterates converge to a first-order stationary point. Numerical experiments demonstrate the effectiveness of the proposed method.

Effcient Projection Onto the Nonconvex $\ell_p$-ball

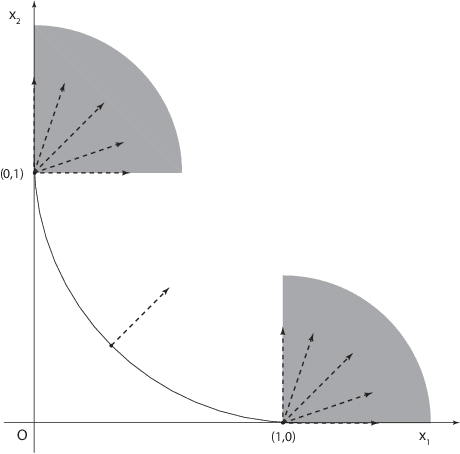
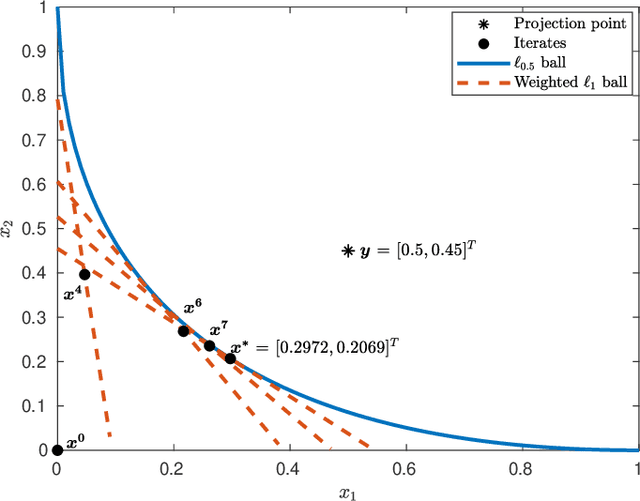
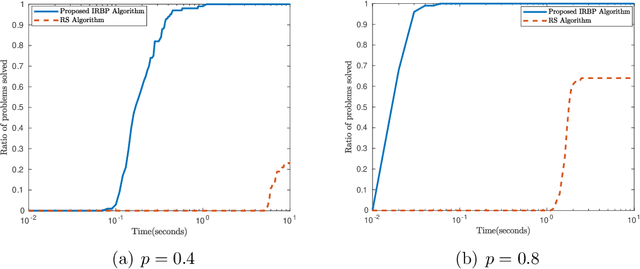
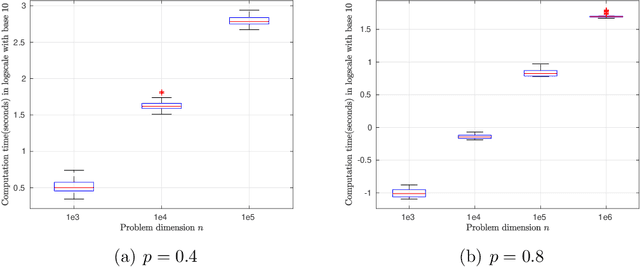
This paper primarily focuses on computing the Euclidean projection of a vector onto the $\ell_{p}$-ball with $p\in(0,1)$. Such a problem emerges as the core building block in many signal processing and machine learning applications because of its ability to promote sparsity, yet it is challenging to solve due to its nonconvex and nonsmooth nature. First-order necessary optimality conditions of this problem are derived using Fr\'echet normal cone. We develop a novel numerical approach for computing the stationary point through solving a sequence of projections onto the reweighted $\ell_{1}$-balls. This method is shown to converge uniquely under mild conditions and has a worst-case $O(1/\sqrt{k})$ convergence rate. Numerical experiments demonstrate the efficiency of our proposed algorithm.

Sparse Optimization for Green Edge AI Inference

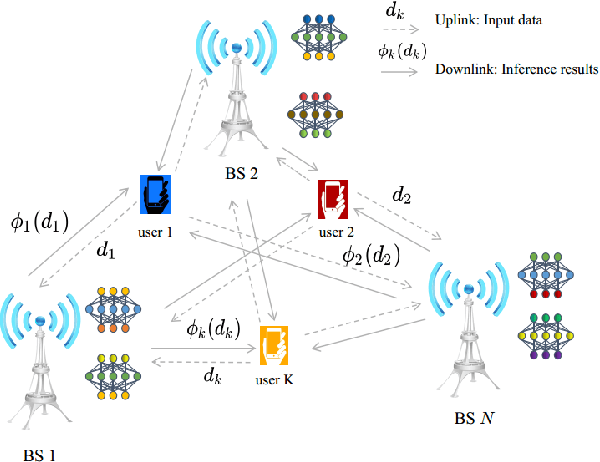
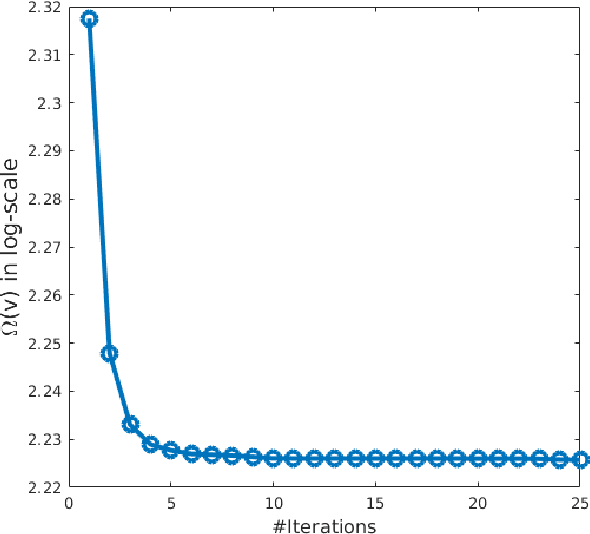
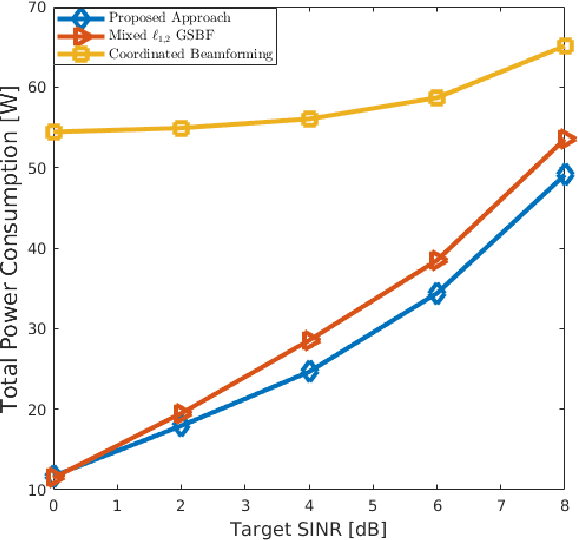
With the rapid upsurge of deep learning tasks at the network edge, effective edge artificial intelligence (AI) inference becomes critical to provide low-latency intelligent services for mobile users via leveraging the edge computing capability. In such scenarios, energy efficiency becomes a primary concern. In this paper, we present a joint inference task selection and downlink beamforming strategy to achieve energy-efficient edge AI inference through minimizing the overall power consumption consisting of both computation and transmission power consumption, yielding a mixed combinatorial optimization problem. By exploiting the inherent connections between the set of task selection and group sparsity structural transmit beamforming vector, we reformulate the optimization as a group sparse beamforming problem. To solve this challenging problem, we propose a log-sum function based three-stage approach. By adopting the log-sum function to enhance the group sparsity, a proximal iteratively reweighted algorithm is developed. Furthermore, we establish the global convergence analysis and provide the ergodic worst-case convergence rate for this algorithm. Simulation results will demonstrate the effectiveness of the proposed approach for improving energy efficiency in edge AI inference systems.