Constrained Optimization Involving Nonconvex $\ell_p$ Norms: Optimality Conditions, Algorithm and Convergence

This paper investigates the optimality conditions for characterizing the local minimizers of the constrained optimization problems involving an $\ell_p$ norm ($0<p<1$) of the variables, which may appear in either the objective or the constraint. This kind of problems have strong applicability to a wide range of areas since usually the $\ell_p$ norm can promote sparse solutions. However, the nonsmooth and non-Lipschtiz nature of the $\ell_p$ norm often cause these problems difficult to analyze and solve. We provide the calculation of the subgradients of the $\ell_p$ norm and the normal cones of the $\ell_p$ ball. For both problems, we derive the first-order necessary conditions under various constraint qualifications. We also derive the sequential optimality conditions for both problems and study the conditions under which these conditions imply the first-order necessary conditions. We point out that the sequential optimality conditions can be easily satisfied for iteratively reweighted algorithms and show that the global convergence can be easily derived using sequential optimality conditions.

Effcient Projection Onto the Nonconvex $\ell_p$-ball

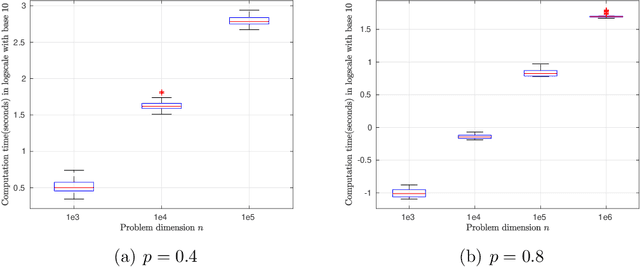
This paper primarily focuses on computing the Euclidean projection of a vector onto the $\ell_{p}$-ball with $p\in(0,1)$. Such a problem emerges as the core building block in many signal processing and machine learning applications because of its ability to promote sparsity, yet it is challenging to solve due to its nonconvex and nonsmooth nature. First-order necessary optimality conditions of this problem are derived using Fr\'echet normal cone. We develop a novel numerical approach for computing the stationary point through solving a sequence of projections onto the reweighted $\ell_{1}$-balls. This method is shown to converge uniquely under mild conditions and has a worst-case $O(1/\sqrt{k})$ convergence rate. Numerical experiments demonstrate the efficiency of our proposed algorithm.

Relating lp regularization and reweighted l1 regularization

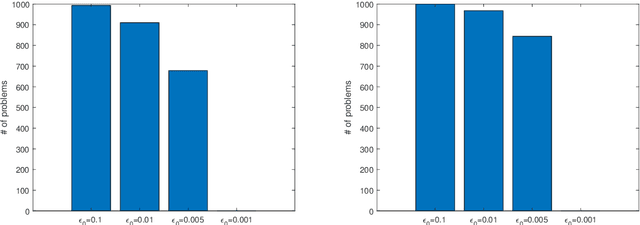
We propose a general framework of iteratively reweighted l1 methods for solving lp regularization problems. We prove that after some iteration k, the iterates generated by the proposed methods have the same support and sign as the limit points, and are bounded away from 0, so that the algorithm behaves like solving a smooth problem in the reduced space. As a result, the global convergence can be easily obtained and an update strategy for the smoothing parameter is proposed which can automatically terminate the updates for zero components. We show that lp regularization problems are locally equivalent to a weighted l1 regularization problem and every optimal point corresponds to a Maximum A Posterior estimation for independently and non-identically distributed Laplace prior parameters. Numerical experiments exhibit the behaviors and the efficiency of our proposed methods.

Inexact Primal-Dual Gradient Projection Methods for Nonlinear Optimization on Convex Set

In this paper, we propose a novel primal-dual inexact gradient projection method for nonlinear optimization problems with convex-set constraint. This method only needs inexact computation of the projections onto the convex set for each iteration, consequently reducing the computational cost for projections per iteration. This feature is attractive especially for solving problems where the projections are computationally not easy to calculate. Global convergence guarantee and O(1/k) ergodic convergence rate of the optimality residual are provided under loose assumptions. We apply our proposed strategy to l1-ball constrained problems. Numerical results exhibit that our inexact gradient projection methods for solving l1-ball constrained problems are more efficient than the exact methods.