Effcient Projection Onto the Nonconvex $\ell_p$-ball

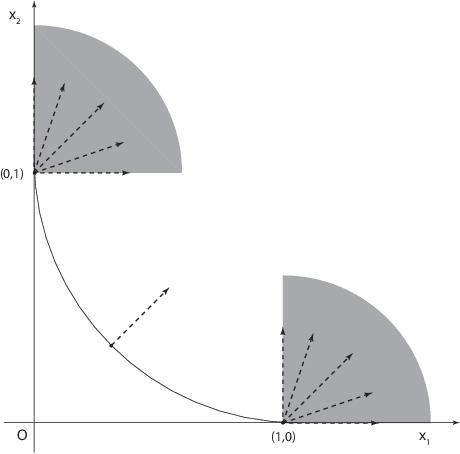
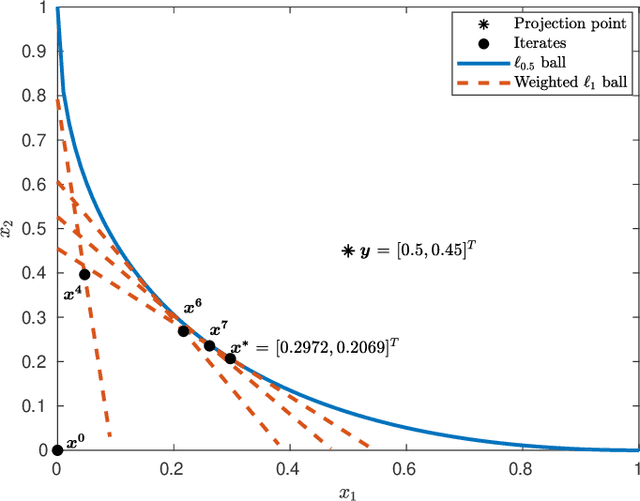
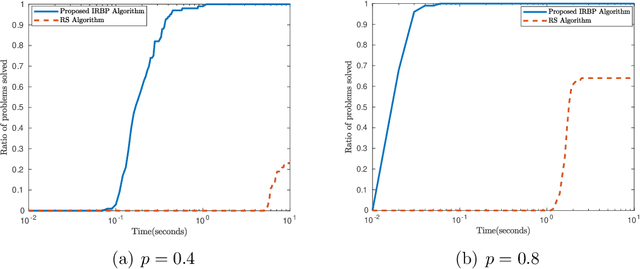
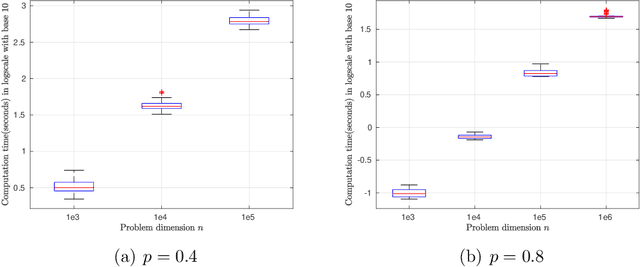
This paper primarily focuses on computing the Euclidean projection of a vector onto the $\ell_{p}$-ball with $p\in(0,1)$. Such a problem emerges as the core building block in many signal processing and machine learning applications because of its ability to promote sparsity, yet it is challenging to solve due to its nonconvex and nonsmooth nature. First-order necessary optimality conditions of this problem are derived using Fr\'echet normal cone. We develop a novel numerical approach for computing the stationary point through solving a sequence of projections onto the reweighted $\ell_{1}$-balls. This method is shown to converge uniquely under mild conditions and has a worst-case $O(1/\sqrt{k})$ convergence rate. Numerical experiments demonstrate the efficiency of our proposed algorithm.