A Screening Strategy for Structured Optimization Involving Nonconvex $\ell_{q,p}$ Regularization
Paper and Code
Aug 02, 2022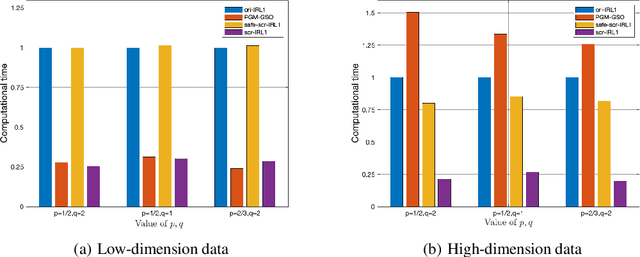

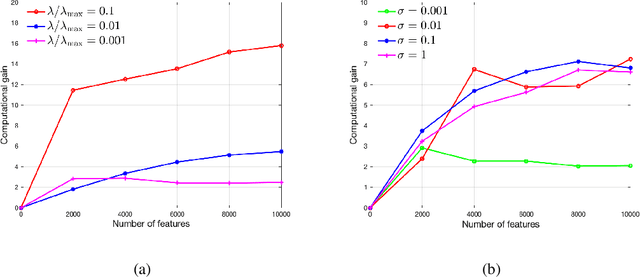
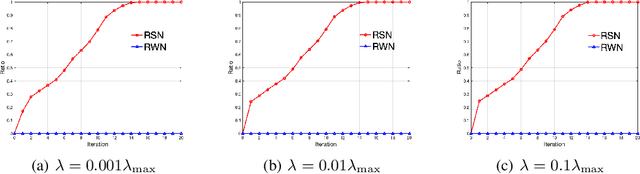
In this paper, we develop a simple yet effective screening rule strategy to improve the computational efficiency in solving structured optimization involving nonconvex $\ell_{q,p}$ regularization. Based on an iteratively reweighted $\ell_1$ (IRL1) framework, the proposed screening rule works like a preprocessing module that potentially removes the inactive groups before starting the subproblem solver, thereby reducing the computational time in total. This is mainly achieved by heuristically exploiting the dual subproblem information during each iteration.Moreover, we prove that our screening rule can remove all inactive variables in a finite number of iterations of the IRL1 method. Numerical experiments illustrate the efficiency of our screening rule strategy compared with several state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge