Efficient Low-rank Identification via Accelerated Iteratively Reweighted Nuclear Norm Minimization

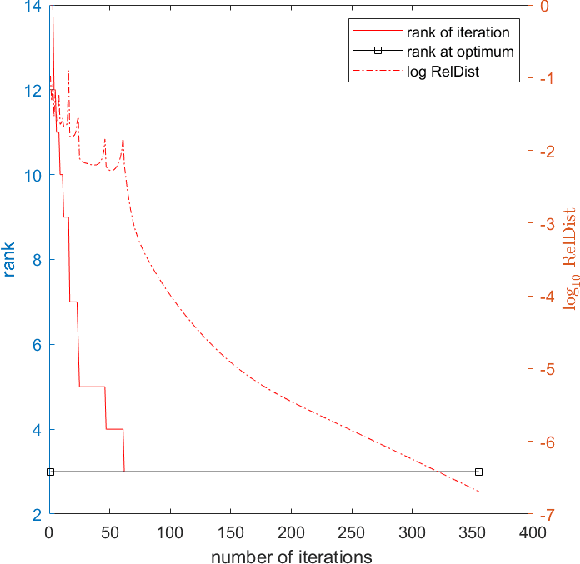
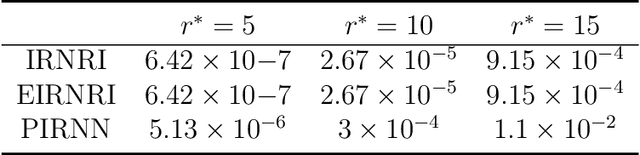
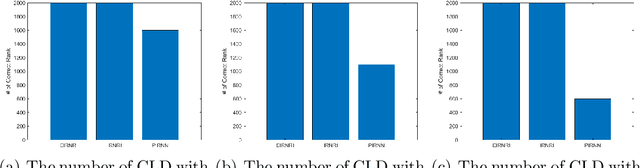
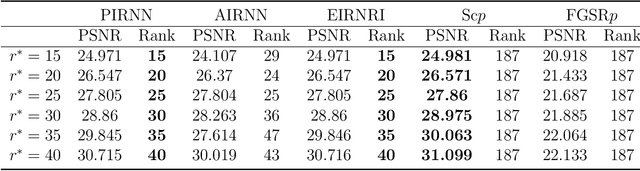
This paper considers the problem of minimizing the sum of a smooth function and the Schatten-$p$ norm of the matrix. Our contribution involves proposing accelerated iteratively reweighted nuclear norm methods designed for solving the nonconvex low-rank minimization problem. Two major novelties characterize our approach. Firstly, the proposed method possesses a rank identification property, enabling the provable identification of the "correct" rank of the stationary point within a finite number of iterations. Secondly, we introduce an adaptive updating strategy for smoothing parameters. This strategy automatically fixes parameters associated with zero singular values as constants upon detecting the "correct" rank while quickly driving the rest of the parameters to zero. This adaptive behavior transforms the algorithm into one that effectively solves smooth problems after a few iterations, setting our work apart from existing iteratively reweighted methods for low-rank optimization. We prove the global convergence of the proposed algorithm, guaranteeing that every limit point of the iterates is a critical point. Furthermore, a local convergence rate analysis is provided under the Kurdyka-{\L}ojasiewicz property. We conduct numerical experiments using both synthetic and real data to showcase our algorithm's efficiency and superiority over existing methods.