An Iteratively Reweighted Method for Sparse Optimization on Nonconvex $\ell_{p}$ Ball
Paper and Code
Apr 07, 2021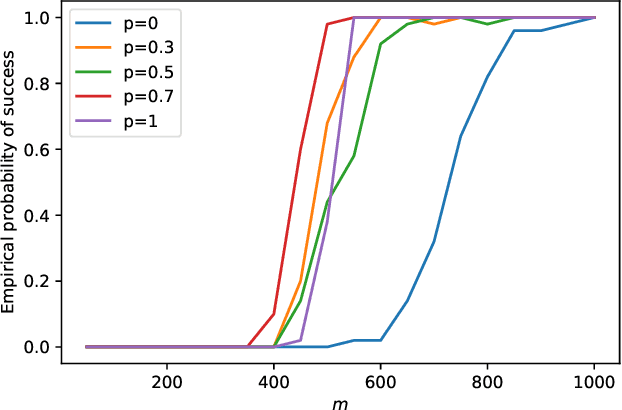
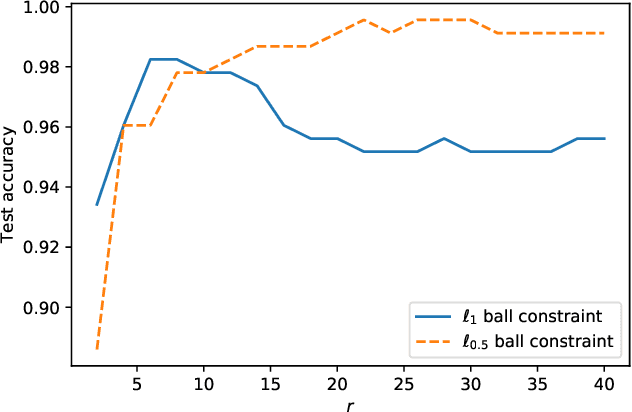
This paper is intended to solve the nonconvex $\ell_{p}$-ball constrained nonlinear optimization problems. An iteratively reweighted method is proposed, which solves a sequence of weighted $\ell_{1}$-ball projection subproblems. At each iteration, the next iterate is obtained by moving along the negative gradient with a stepsize and then projecting the resulted point onto the weighted $\ell_{1}$ ball to approximate the $\ell_{p}$ ball. Specifically, if the current iterate is in the interior of the feasible set, then the weighted $\ell_{1}$ ball is formed by linearizing the $\ell_{p}$ norm at the current iterate. If the current iterate is on the boundary of the feasible set, then the weighted $\ell_{1}$ ball is formed differently by keeping those zero components in the current iterate still zero. In our analysis, we prove that the generated iterates converge to a first-order stationary point. Numerical experiments demonstrate the effectiveness of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge