A GPU Implementation of Multi-Guiding Spark Fireworks Algorithm for Efficient Black-Box Neural Network Optimization

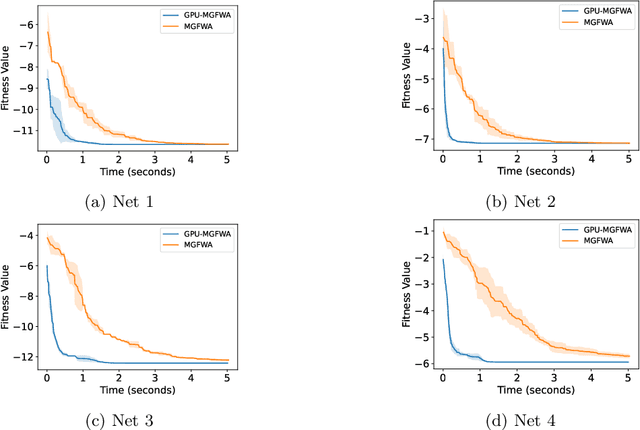
Swarm intelligence optimization algorithms have gained significant attention due to their ability to solve complex optimization problems. However, the efficiency of optimization in large-scale problems limits the use of related methods. This paper presents a GPU-accelerated version of the Multi-Guiding Spark Fireworks Algorithm (MGFWA), which significantly improves the computational efficiency compared to its traditional CPU-based counterpart. We benchmark the GPU-MGFWA on several neural network black-box optimization problems and demonstrate its superior performance in terms of both speed and solution quality. By leveraging the parallel processing power of modern GPUs, the proposed GPU-MGFWA results in faster convergence and reduced computation time for large-scale optimization tasks. The proposed implementation offers a promising approach to accelerate swarm intelligence algorithms, making them more suitable for real-time applications and large-scale industrial problems. Source code is released at https://github.com/mxxxr/MGFWA.

Exploring Large Language Model based Intelligent Agents: Definitions, Methods, and Prospects

Intelligent agents stand out as a potential path toward artificial general intelligence (AGI). Thus, researchers have dedicated significant effort to diverse implementations for them. Benefiting from recent progress in large language models (LLMs), LLM-based agents that use universal natural language as an interface exhibit robust generalization capabilities across various applications -- from serving as autonomous general-purpose task assistants to applications in coding, social, and economic domains, LLM-based agents offer extensive exploration opportunities. This paper surveys current research to provide an in-depth overview of LLM-based intelligent agents within single-agent and multi-agent systems. It covers their definitions, research frameworks, and foundational components such as their composition, cognitive and planning methods, tool utilization, and responses to environmental feedback. We also delve into the mechanisms of deploying LLM-based agents in multi-agent systems, including multi-role collaboration, message passing, and strategies to alleviate communication issues between agents. The discussions also shed light on popular datasets and application scenarios. We conclude by envisioning prospects for LLM-based agents, considering the evolving landscape of AI and natural language processing.

Implementing Randomized Matrix Algorithms in Parallel and Distributed Environments

In this era of large-scale data, distributed systems built on top of clusters of commodity hardware provide cheap and reliable storage and scalable processing of massive data. Here, we review recent work on developing and implementing randomized matrix algorithms in large-scale parallel and distributed environments. Randomized algorithms for matrix problems have received a great deal of attention in recent years, thus far typically either in theory or in machine learning applications or with implementations on a single machine. Our main focus is on the underlying theory and practical implementation of random projection and random sampling algorithms for very large very overdetermined (i.e., overconstrained) $\ell_1$ and $\ell_2$ regression problems. Randomization can be used in one of two related ways: either to construct sub-sampled problems that can be solved, exactly or approximately, with traditional numerical methods; or to construct preconditioned versions of the original full problem that are easier to solve with traditional iterative algorithms. Theoretical results demonstrate that in near input-sparsity time and with only a few passes through the data one can obtain very strong relative-error approximate solutions, with high probability. Empirical results highlight the importance of various trade-offs (e.g., between the time to construct an embedding and the conditioning quality of the embedding, between the relative importance of computation versus communication, etc.) and demonstrate that $\ell_1$ and $\ell_2$ regression problems can be solved to low, medium, or high precision in existing distributed systems on up to terabyte-sized data.

MLlib: Machine Learning in Apache Spark

Apache Spark is a popular open-source platform for large-scale data processing that is well-suited for iterative machine learning tasks. In this paper we present MLlib, Spark's open-source distributed machine learning library. MLlib provides efficient functionality for a wide range of learning settings and includes several underlying statistical, optimization, and linear algebra primitives. Shipped with Spark, MLlib supports several languages and provides a high-level API that leverages Spark's rich ecosystem to simplify the development of end-to-end machine learning pipelines. MLlib has experienced a rapid growth due to its vibrant open-source community of over 140 contributors, and includes extensive documentation to support further growth and to let users quickly get up to speed.

The Fast Cauchy Transform and Faster Robust Linear Regression

We provide fast algorithms for overconstrained $\ell_p$ regression and related problems: for an $n\times d$ input matrix $A$ and vector $b\in\mathbb{R}^n$, in $O(nd\log n)$ time we reduce the problem $\min_{x\in\mathbb{R}^d} \|Ax-b\|_p$ to the same problem with input matrix $\tilde A$ of dimension $s \times d$ and corresponding $\tilde b$ of dimension $s\times 1$. Here, $\tilde A$ and $\tilde b$ are a coreset for the problem, consisting of sampled and rescaled rows of $A$ and $b$; and $s$ is independent of $n$ and polynomial in $d$. Our results improve on the best previous algorithms when $n\gg d$, for all $p\in[1,\infty)$ except $p=2$. We also provide a suite of improved results for finding well-conditioned bases via ellipsoidal rounding, illustrating tradeoffs between running time and conditioning quality, including a one-pass conditioning algorithm for general $\ell_p$ problems. We also provide an empirical evaluation of implementations of our algorithms for $p=1$, comparing them with related algorithms. Our empirical results show that, in the asymptotic regime, the theory is a very good guide to the practical performance of these algorithms. Our algorithms use our faster constructions of well-conditioned bases for $\ell_p$ spaces and, for $p=1$, a fast subspace embedding of independent interest that we call the Fast Cauchy Transform: a distribution over matrices $\Pi:\mathbb{R}^n\mapsto \mathbb{R}^{O(d\log d)}$, found obliviously to $A$, that approximately preserves the $\ell_1$ norms: that is, with large probability, simultaneously for all $x$, $\|Ax\|_1 \approx \|\Pi Ax\|_1$, with distortion $O(d^{2+\eta})$, for an arbitrarily small constant $\eta>0$; and, moreover, $\Pi A$ can be computed in $O(nd\log d)$ time. The techniques underlying our Fast Cauchy Transform include fast Johnson-Lindenstrauss transforms, low-coherence matrices, and rescaling by Cauchy random variables.

Quantile Regression for Large-scale Applications

Quantile regression is a method to estimate the quantiles of the conditional distribution of a response variable, and as such it permits a much more accurate portrayal of the relationship between the response variable and observed covariates than methods such as Least-squares or Least Absolute Deviations regression. It can be expressed as a linear program, and, with appropriate preprocessing, interior-point methods can be used to find a solution for moderately large problems. Dealing with very large problems, \emph(e.g.), involving data up to and beyond the terabyte regime, remains a challenge. Here, we present a randomized algorithm that runs in nearly linear time in the size of the input and that, with constant probability, computes a $(1+\epsilon)$ approximate solution to an arbitrary quantile regression problem. As a key step, our algorithm computes a low-distortion subspace-preserving embedding with respect to the loss function of quantile regression. Our empirical evaluation illustrates that our algorithm is competitive with the best previous work on small to medium-sized problems, and that in addition it can be implemented in MapReduce-like environments and applied to terabyte-sized problems.