William Fithian
Forecasting Rare Language Model Behaviors
Feb 24, 2025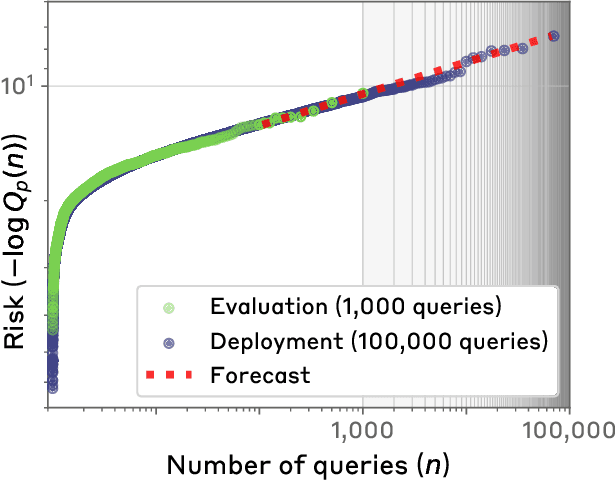
Abstract:Standard language model evaluations can fail to capture risks that emerge only at deployment scale. For example, a model may produce safe responses during a small-scale beta test, yet reveal dangerous information when processing billions of requests at deployment. To remedy this, we introduce a method to forecast potential risks across orders of magnitude more queries than we test during evaluation. We make forecasts by studying each query's elicitation probability -- the probability the query produces a target behavior -- and demonstrate that the largest observed elicitation probabilities predictably scale with the number of queries. We find that our forecasts can predict the emergence of diverse undesirable behaviors -- such as assisting users with dangerous chemical synthesis or taking power-seeking actions -- across up to three orders of magnitude of query volume. Our work enables model developers to proactively anticipate and patch rare failures before they manifest during large-scale deployments.
A Flexible Defense Against the Winner's Curse
Nov 27, 2024Abstract:Across science and policy, decision-makers often need to draw conclusions about the best candidate among competing alternatives. For instance, researchers may seek to infer the effectiveness of the most successful treatment or determine which demographic group benefits most from a specific treatment. Similarly, in machine learning, practitioners are often interested in the population performance of the model that performs best empirically. However, cherry-picking the best candidate leads to the winner's curse: the observed performance for the winner is biased upwards, rendering conclusions based on standard measures of uncertainty invalid. We introduce the zoom correction, a novel approach for valid inference on the winner. Our method is flexible: it can be employed in both parametric and nonparametric settings, can handle arbitrary dependencies between candidates, and automatically adapts to the level of selection bias. The method easily extends to important related problems, such as inference on the top k winners, inference on the value and identity of the population winner, and inference on "near-winners."
AdaPT-GMM: Powerful and robust covariate-assisted multiple testing
Jun 30, 2021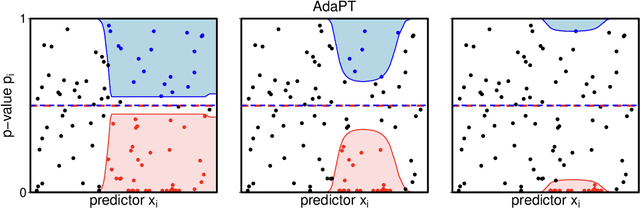
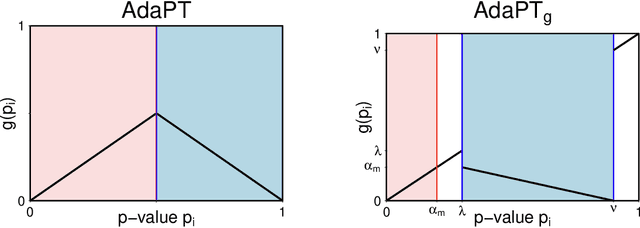
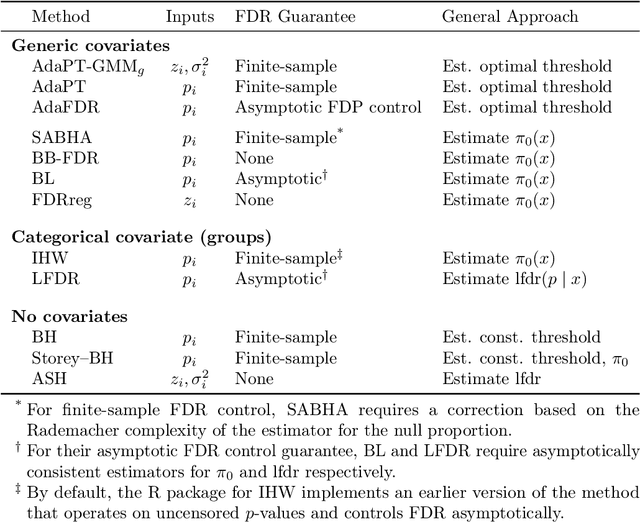
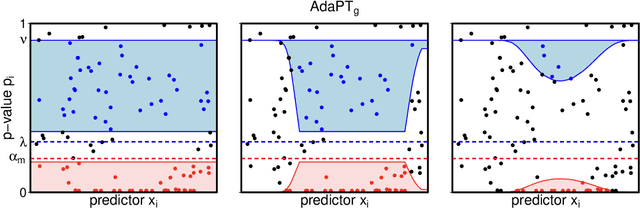
Abstract:We propose a new empirical Bayes method for covariate-assisted multiple testing with false discovery rate (FDR) control, where we model the local false discovery rate for each hypothesis as a function of both its covariates and p-value. Our method refines the adaptive p-value thresholding (AdaPT) procedure by generalizing its masking scheme to reduce the bias and variance of its false discovery proportion estimator, improving the power when the rejection set is small or some null p-values concentrate near 1. We also introduce a Gaussian mixture model for the conditional distribution of the test statistics given covariates, modeling the mixing proportions with a generic user-specified classifier, which we implement using a two-layer neural network. Like AdaPT, our method provably controls the FDR in finite samples even if the classifier or the Gaussian mixture model is misspecified. We show in extensive simulations and real data examples that our new method, which we call AdaPT-GMM, consistently delivers high power relative to competing state-of-the-art methods. In particular, it performs well in scenarios where AdaPT is underpowered, and is especially well-suited for testing composite null hypothesis, such as whether the effect size exceeds a practical significance threshold.
Flexible Low-Rank Statistical Modeling with Side Information
Aug 22, 2017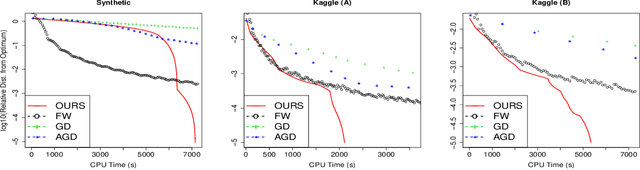
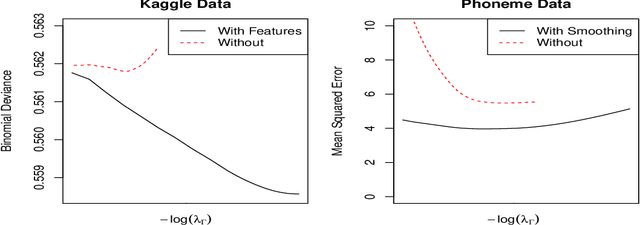
Abstract:We propose a general framework for reduced-rank modeling of matrix-valued data. By applying a generalized nuclear norm penalty we can directly model low-dimensional latent variables associated with rows and columns. Our framework flexibly incorporates row and column features, smoothing kernels, and other sources of side information by penalizing deviations from the row and column models. Moreover, a large class of these models can be estimated scalably using convex optimization. The computational bottleneck in each case is one singular value decomposition per iteration of a large but easy-to-apply matrix. Our framework generalizes traditional convex matrix completion and multi-task learning methods as well as maximum a posteriori estimation under a large class of popular hierarchical Bayesian models.
Data Augmentation via Levy Processes
Mar 21, 2016
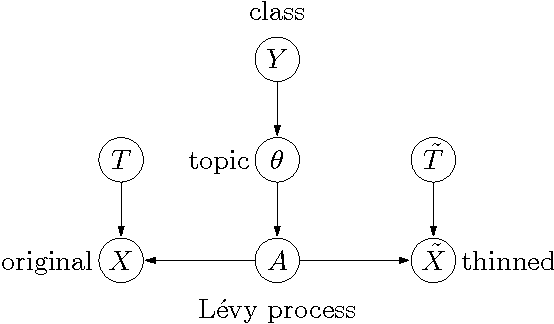
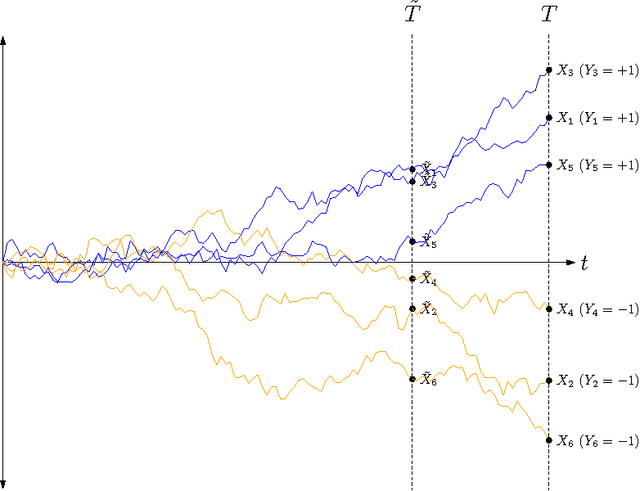
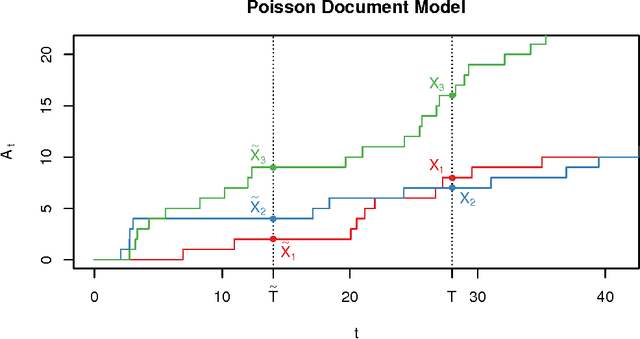
Abstract:If a document is about travel, we may expect that short snippets of the document should also be about travel. We introduce a general framework for incorporating these types of invariances into a discriminative classifier. The framework imagines data as being drawn from a slice of a Levy process. If we slice the Levy process at an earlier point in time, we obtain additional pseudo-examples, which can be used to train the classifier. We show that this scheme has two desirable properties: it preserves the Bayes decision boundary, and it is equivalent to fitting a generative model in the limit where we rewind time back to 0. Our construction captures popular schemes such as Gaussian feature noising and dropout training, as well as admitting new generalizations.
Selective Sequential Model Selection
Dec 08, 2015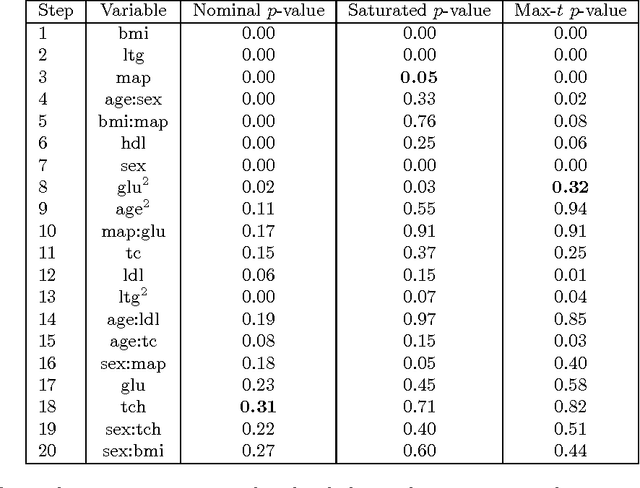
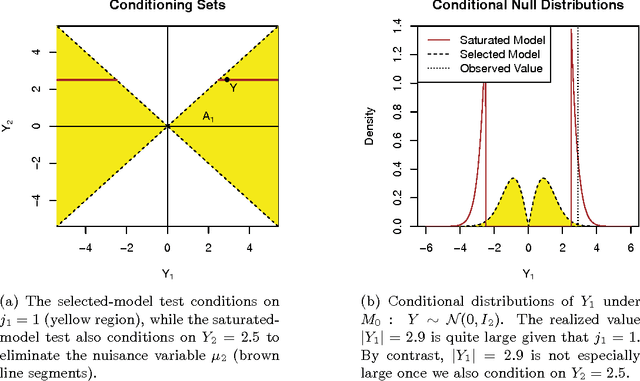
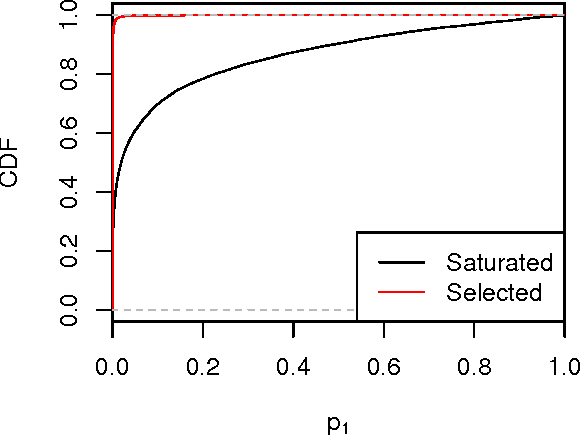
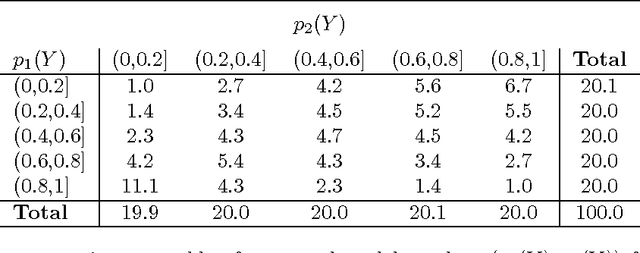
Abstract:Many model selection algorithms produce a path of fits specifying a sequence of increasingly complex models. Given such a sequence and the data used to produce them, we consider the problem of choosing the least complex model that is not falsified by the data. Extending the selected-model tests of Fithian et al. (2014), we construct p-values for each step in the path which account for the adaptive selection of the model path using the data. In the case of linear regression, we propose two specific tests, the max-t test for forward stepwise regression (generalizing a proposal of Buja and Brown (2014)), and the next-entry test for the lasso. These tests improve on the power of the saturated-model test of Tibshirani et al. (2014), sometimes dramatically. In addition, our framework extends beyond linear regression to a much more general class of parametric and nonparametric model selection problems. To select a model, we can feed our single-step p-values as inputs into sequential stopping rules such as those proposed by G'Sell et al. (2013) and Li and Barber (2015), achieving control of the familywise error rate or false discovery rate (FDR) as desired. The FDR-controlling rules require the null p-values to be independent of each other and of the non-null p-values, a condition not satisfied by the saturated-model p-values of Tibshirani et al. (2014). We derive intuitive and general sufficient conditions for independence, and show that our proposed constructions yield independent p-values.
Altitude Training: Strong Bounds for Single-Layer Dropout
Oct 31, 2014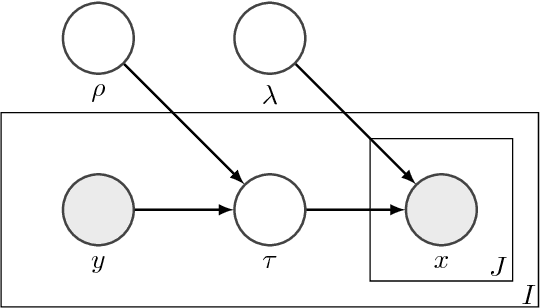
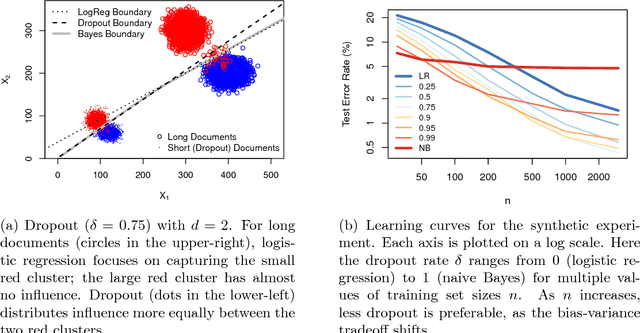
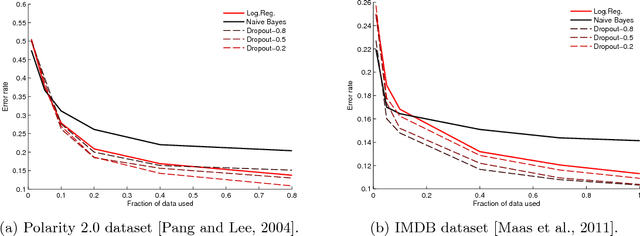
Abstract:Dropout training, originally designed for deep neural networks, has been successful on high-dimensional single-layer natural language tasks. This paper proposes a theoretical explanation for this phenomenon: we show that, under a generative Poisson topic model with long documents, dropout training improves the exponent in the generalization bound for empirical risk minimization. Dropout achieves this gain much like a marathon runner who practices at altitude: once a classifier learns to perform reasonably well on training examples that have been artificially corrupted by dropout, it will do very well on the uncorrupted test set. We also show that, under similar conditions, dropout preserves the Bayes decision boundary and should therefore induce minimal bias in high dimensions.
Local case-control sampling: Efficient subsampling in imbalanced data sets
Sep 23, 2014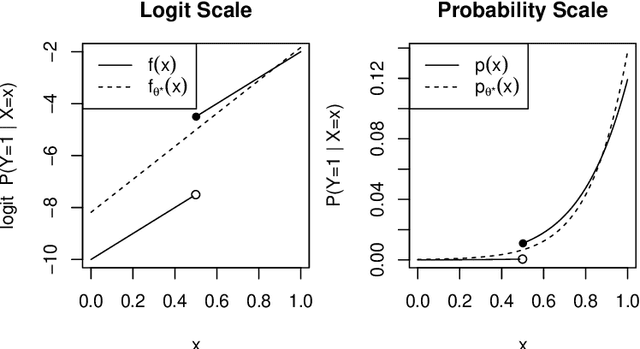
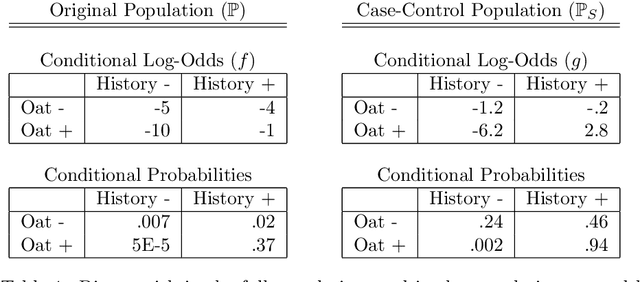
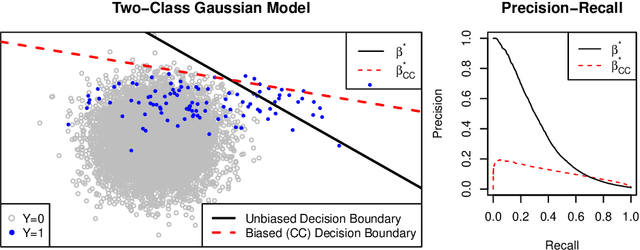
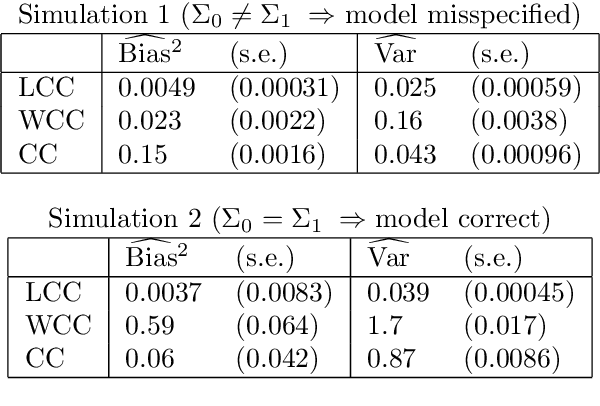
Abstract:For classification problems with significant class imbalance, subsampling can reduce computational costs at the price of inflated variance in estimating model parameters. We propose a method for subsampling efficiently for logistic regression by adjusting the class balance locally in feature space via an accept-reject scheme. Our method generalizes standard case-control sampling, using a pilot estimate to preferentially select examples whose responses are conditionally rare given their features. The biased subsampling is corrected by a post-hoc analytic adjustment to the parameters. The method is simple and requires one parallelizable scan over the full data set. Standard case-control sampling is inconsistent under model misspecification for the population risk-minimizing coefficients $\theta^*$. By contrast, our estimator is consistent for $\theta^*$ provided that the pilot estimate is. Moreover, under correct specification and with a consistent, independent pilot estimate, our estimator has exactly twice the asymptotic variance of the full-sample MLE - even if the selected subsample comprises a miniscule fraction of the full data set, as happens when the original data are severely imbalanced. The factor of two improves to $1+\frac{1}{c}$ if we multiply the baseline acceptance probabilities by $c>1$ (and weight points with acceptance probability greater than 1), taking roughly $\frac{1+c}{2}$ times as many data points into the subsample. Experiments on simulated and real data show that our method can substantially outperform standard case-control subsampling.
* Published in at http://dx.doi.org/10.1214/14-AOS1220 the Annals of Statistics (http://www.imstat.org/aos/) by the Institute of Mathematical Statistics (http://www.imstat.org)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge