Total Variation Classes Beyond 1d: Minimax Rates, and the Limitations of Linear Smoothers

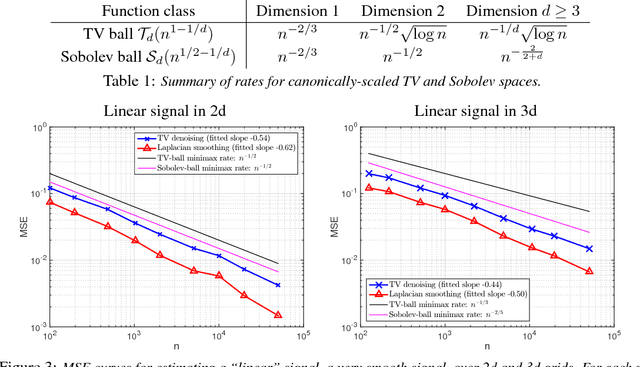
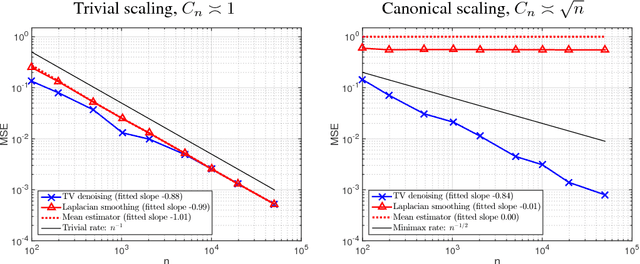
We consider the problem of estimating a function defined over $n$ locations on a $d$-dimensional grid (having all side lengths equal to $n^{1/d}$). When the function is constrained to have discrete total variation bounded by $C_n$, we derive the minimax optimal (squared) $\ell_2$ estimation error rate, parametrized by $n$ and $C_n$. Total variation denoising, also known as the fused lasso, is seen to be rate optimal. Several simpler estimators exist, such as Laplacian smoothing and Laplacian eigenmaps. A natural question is: can these simpler estimators perform just as well? We prove that these estimators, and more broadly all estimators given by linear transformations of the input data, are suboptimal over the class of functions with bounded variation. This extends fundamental findings of Donoho and Johnstone [1998] on 1-dimensional total variation spaces to higher dimensions. The implication is that the computationally simpler methods cannot be used for such sophisticated denoising tasks, without sacrificing statistical accuracy. We also derive minimax rates for discrete Sobolev spaces over $d$-dimensional grids, which are, in some sense, smaller than the total variation function spaces. Indeed, these are small enough spaces that linear estimators can be optimal---and a few well-known ones are, such as Laplacian smoothing and Laplacian eigenmaps, as we show. Lastly, we investigate the problem of adaptivity of the total variation denoiser to these smaller Sobolev function spaces.

Selective Sequential Model Selection

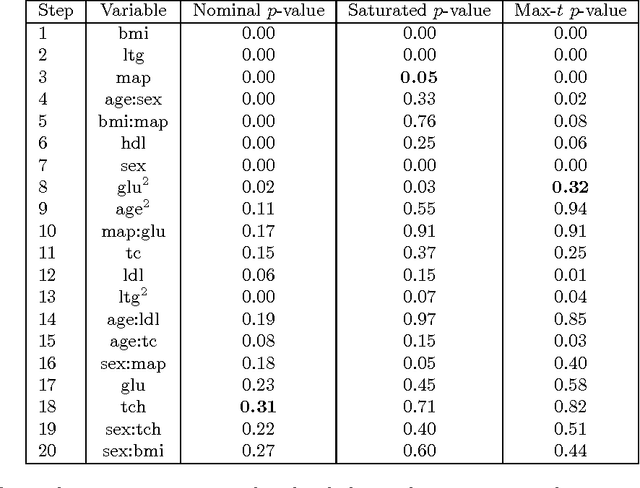
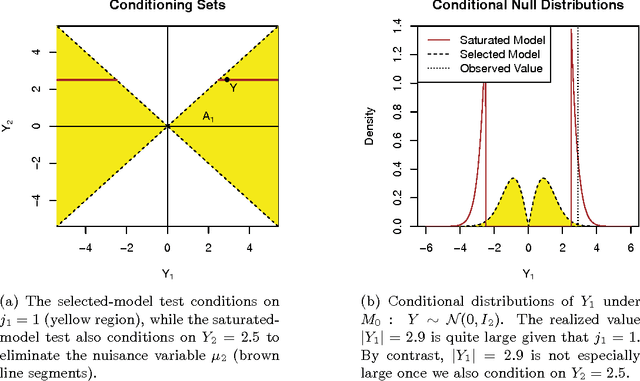
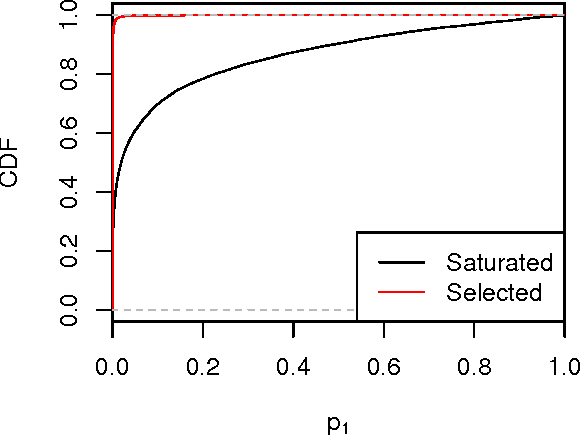
Many model selection algorithms produce a path of fits specifying a sequence of increasingly complex models. Given such a sequence and the data used to produce them, we consider the problem of choosing the least complex model that is not falsified by the data. Extending the selected-model tests of Fithian et al. (2014), we construct p-values for each step in the path which account for the adaptive selection of the model path using the data. In the case of linear regression, we propose two specific tests, the max-t test for forward stepwise regression (generalizing a proposal of Buja and Brown (2014)), and the next-entry test for the lasso. These tests improve on the power of the saturated-model test of Tibshirani et al. (2014), sometimes dramatically. In addition, our framework extends beyond linear regression to a much more general class of parametric and nonparametric model selection problems. To select a model, we can feed our single-step p-values as inputs into sequential stopping rules such as those proposed by G'Sell et al. (2013) and Li and Barber (2015), achieving control of the familywise error rate or false discovery rate (FDR) as desired. The FDR-controlling rules require the null p-values to be independent of each other and of the non-null p-values, a condition not satisfied by the saturated-model p-values of Tibshirani et al. (2014). We derive intuitive and general sufficient conditions for independence, and show that our proposed constructions yield independent p-values.

Efficient Implementations of the Generalized Lasso Dual Path Algorithm

We consider efficient implementations of the generalized lasso dual path algorithm of Tibshirani and Taylor (2011). We first describe a generic approach that covers any penalty matrix D and any (full column rank) matrix X of predictor variables. We then describe fast implementations for the special cases of trend filtering problems, fused lasso problems, and sparse fused lasso problems, both with X=I and a general matrix X. These specialized implementations offer a considerable improvement over the generic implementation, both in terms of numerical stability and efficiency of the solution path computation. These algorithms are all available for use in the genlasso R package, which can be found in the CRAN repository.