Flexible Low-Rank Statistical Modeling with Side Information
Paper and Code
Aug 22, 2017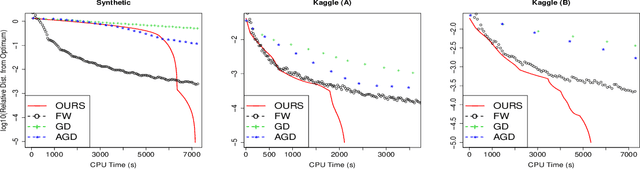
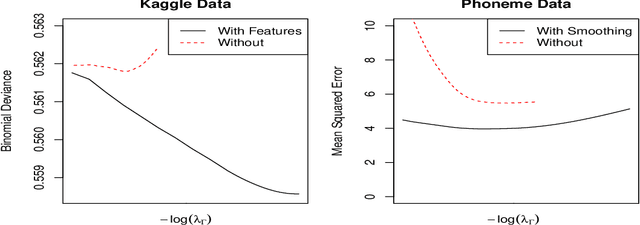
We propose a general framework for reduced-rank modeling of matrix-valued data. By applying a generalized nuclear norm penalty we can directly model low-dimensional latent variables associated with rows and columns. Our framework flexibly incorporates row and column features, smoothing kernels, and other sources of side information by penalizing deviations from the row and column models. Moreover, a large class of these models can be estimated scalably using convex optimization. The computational bottleneck in each case is one singular value decomposition per iteration of a large but easy-to-apply matrix. Our framework generalizes traditional convex matrix completion and multi-task learning methods as well as maximum a posteriori estimation under a large class of popular hierarchical Bayesian models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge