Altitude Training: Strong Bounds for Single-Layer Dropout
Paper and Code
Oct 31, 2014
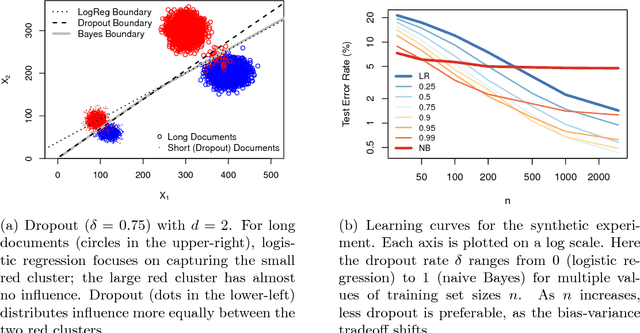
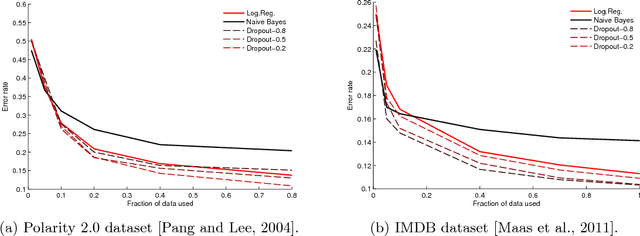
Dropout training, originally designed for deep neural networks, has been successful on high-dimensional single-layer natural language tasks. This paper proposes a theoretical explanation for this phenomenon: we show that, under a generative Poisson topic model with long documents, dropout training improves the exponent in the generalization bound for empirical risk minimization. Dropout achieves this gain much like a marathon runner who practices at altitude: once a classifier learns to perform reasonably well on training examples that have been artificially corrupted by dropout, it will do very well on the uncorrupted test set. We also show that, under similar conditions, dropout preserves the Bayes decision boundary and should therefore induce minimal bias in high dimensions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge