LCGC: Learning from Consistency Gradient Conflicting for Class-Imbalanced Semi-Supervised Debiasing

Classifiers often learn to be biased corresponding to the class-imbalanced dataset, especially under the semi-supervised learning (SSL) set. While previous work tries to appropriately re-balance the classifiers by subtracting a class-irrelevant image's logit, but lacks a firm theoretical basis. We theoretically analyze why exploiting a baseline image can refine pseudo-labels and prove that the black image is the best choice. We also indicated that as the training process deepens, the pseudo-labels before and after refinement become closer. Based on this observation, we propose a debiasing scheme dubbed LCGC, which Learning from Consistency Gradient Conflicting, by encouraging biased class predictions during training. We intentionally update the pseudo-labels whose gradient conflicts with the debiased logits, representing the optimization direction offered by the over-imbalanced classifier predictions. Then, we debiased the predictions by subtracting the baseline image logits during testing. Extensive experiments demonstrate that LCGC can significantly improve the prediction accuracy of existing CISSL models on public benchmarks.

Enhancing the Reasoning Capabilities of Small Language Models via Solution Guidance Fine-Tuning

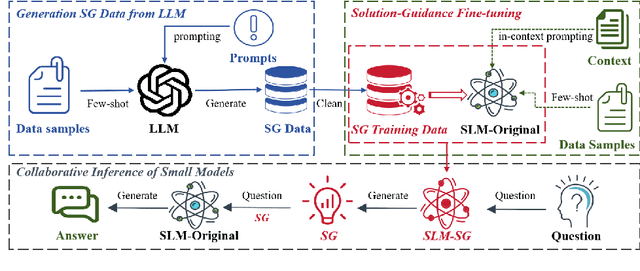
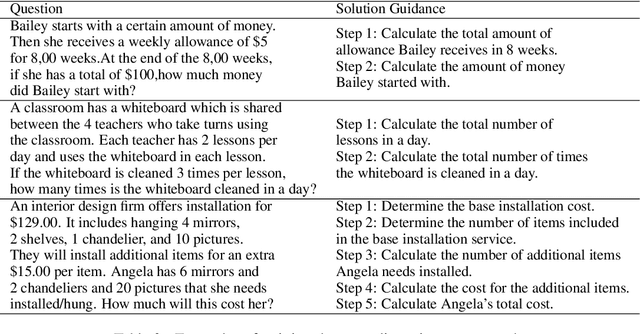
Large language models (LLMs) have demonstrated remarkable performance across a wide range of tasks. Advances in prompt engineering and fine-tuning techniques have further enhanced their ability to address complex reasoning challenges. However, these advanced capabilities are often exclusive to models exceeding 100 billion parameters. Although Chain-of-Thought (CoT) fine-tuning methods have been explored for smaller models (under 10 billion parameters), they typically depend on extensive CoT training data, which can introduce inconsistencies and limit effectiveness in low-data settings. To overcome these limitations, this paper introduce a new reasoning strategy Solution Guidance (SG) and a plug-and-play training paradigm Solution-Guidance Fine-Tuning (SGFT) for enhancing the reasoning capabilities of small language models. SG focuses on problem understanding and decomposition at the semantic and logical levels, rather than specific computations, which can effectively improve the SLMs' generalization and reasoning abilities. With only a small amount of SG training data, SGFT can fine-tune a SLM to produce accurate problem-solving guidances, which can then be flexibly fed to any SLM as prompts, enabling it to generate correct answers directly. Experimental results demonstrate that our method significantly improves the performance of SLMs on various reasoning tasks, enhancing both their practicality and efficiency within resource-constrained environments.

LatentSync: Audio Conditioned Latent Diffusion Models for Lip Sync

We present LatentSync, an end-to-end lip sync framework based on audio conditioned latent diffusion models without any intermediate motion representation, diverging from previous diffusion-based lip sync methods based on pixel space diffusion or two-stage generation. Our framework can leverage the powerful capabilities of Stable Diffusion to directly model complex audio-visual correlations. Additionally, we found that the diffusion-based lip sync methods exhibit inferior temporal consistency due to the inconsistency in the diffusion process across different frames. We propose Temporal REPresentation Alignment (TREPA) to enhance temporal consistency while preserving lip-sync accuracy. TREPA uses temporal representations extracted by large-scale self-supervised video models to align the generated frames with the ground truth frames. Furthermore, we observe the commonly encountered SyncNet convergence issue and conduct comprehensive empirical studies, identifying key factors affecting SyncNet convergence in terms of model architecture, training hyperparameters, and data preprocessing methods. We significantly improve the accuracy of SyncNet from 91% to 94% on the HDTF test set. Since we did not change the overall training framework of SyncNet, our experience can also be applied to other lip sync and audio-driven portrait animation methods that utilize SyncNet. Based on the above innovations, our method outperforms state-of-the-art lip sync methods across various metrics on the HDTF and VoxCeleb2 datasets.

LOCAL: Learning with Orientation Matrix to Infer Causal Structure from Time Series Data

Discovering the underlying Directed Acyclic Graph (DAG) from time series observational data is highly challenging due to the dynamic nature and complex nonlinear interactions between variables. Existing methods often struggle with inefficiency and the handling of high-dimensional data. To address these research gap, we propose LOCAL, a highly efficient, easy-to-implement, and constraint-free method for recovering dynamic causal structures. LOCAL is the first attempt to formulate a quasi-maximum likelihood-based score function for learning the dynamic DAG equivalent to the ground truth. On this basis, we propose two adaptive modules for enhancing the algebraic characterization of acyclicity with new capabilities: Asymptotic Causal Mask Learning (ACML) and Dynamic Graph Parameter Learning (DGPL). ACML generates causal masks using learnable priority vectors and the Gumbel-Sigmoid function, ensuring the creation of DAGs while optimizing computational efficiency. DGPL transforms causal learning into decomposed matrix products, capturing the dynamic causal structure of high-dimensional data and enhancing interpretability. Extensive experiments on synthetic and real-world datasets demonstrate that LOCAL significantly outperforms existing methods, and highlight LOCAL's potential as a robust and efficient method for dynamic causal discovery. Our code will be available soon.

LinBridge: A Learnable Framework for Interpreting Nonlinear Neural Encoding Models

Neural encoding of artificial neural networks (ANNs) links their computational representations to brain responses, offering insights into how the brain processes information. Current studies mostly use linear encoding models for clarity, even though brain responses are often nonlinear. This has sparked interest in developing nonlinear encoding models that are still interpretable. To address this problem, we propose LinBridge, a learnable and flexible framework based on Jacobian analysis for interpreting nonlinear encoding models. LinBridge posits that the nonlinear mapping between ANN representations and neural responses can be factorized into a linear inherent component that approximates the complex nonlinear relationship, and a mapping bias that captures sample-selective nonlinearity. The Jacobian matrix, which reflects output change rates relative to input, enables the analysis of sample-selective mapping in nonlinear models. LinBridge employs a self-supervised learning strategy to extract both the linear inherent component and nonlinear mapping biases from the Jacobian matrices of the test set, allowing it to adapt effectively to various nonlinear encoding models. We validate the LinBridge framework in the scenario of neural visual encoding, using computational visual representations from CLIP-ViT to predict brain activity recorded via functional magnetic resonance imaging (fMRI). Our experimental results demonstrate that: 1) the linear inherent component extracted by LinBridge accurately reflects the complex mappings of nonlinear neural encoding models; 2) the sample-selective mapping bias elucidates the variability of nonlinearity across different levels of the visual processing hierarchy. This study presents a novel tool for interpreting nonlinear neural encoding models and offers fresh evidence about hierarchical nonlinearity distribution in the visual cortex.