Cut the Deadwood Out: Post-Training Model Purification with Selective Module Substitution

The success of DNNs often depends on training with large-scale datasets, but building such datasets is both expensive and challenging. Consequently, public datasets from open-source platforms like HuggingFace have become popular, posing significant risks of data poisoning attacks. Existing backdoor defenses in NLP primarily focus on identifying and removing poisoned samples; however, purifying a backdoored model with these sample-cleaning approaches typically requires expensive retraining. Therefore, we propose Greedy Module Substitution (GMS), which identifies and substitutes ''deadwood'' modules (i.e., components critical to backdoor pathways) in a backdoored model to purify it. Our method relaxes the common dependency of prior model purification methods on clean datasets or clean auxiliary models. When applied to RoBERTa-large under backdoor attacks, GMS demonstrates strong effectiveness across various settings, particularly against widely recognized challenging attacks like LWS, achieving a post-purification attack success rate (ASR) of 9.7% on SST-2 compared to 58.8% for the best baseline approach.

Segmentation-aware Prior Assisted Joint Global Information Aggregated 3D Building Reconstruction

Multi-View Stereo plays a pivotal role in civil engineering by facilitating 3D modeling, precise engineering surveying, quantitative analysis, as well as monitoring and maintenance. It serves as a valuable tool, offering high-precision and real-time spatial information crucial for various engineering projects. However, Multi-View Stereo algorithms encounter challenges in reconstructing weakly-textured regions within large-scale building scenes. In these areas, the stereo matching of pixels often fails, leading to inaccurate depth estimations. Based on the Segment Anything Model and RANSAC algorithm, we propose an algorithm that accurately segments weakly-textured regions and constructs their plane priors. These plane priors, combined with triangulation priors, form a reliable prior candidate set. Additionally, we introduce a novel global information aggregation cost function. This function selects optimal plane prior information based on global information in the prior candidate set, constrained by geometric consistency during the depth estimation update process. Experimental results on both the ETH3D benchmark dataset, aerial dataset, building dataset and real scenarios substantiate the superior performance of our method in producing 3D building models compared to other state-of-the-art methods. In summary, our work aims to enhance the completeness and density of 3D building reconstruction, carrying implications for broader applications in urban planning and virtual reality.

Operator Feature Neural Network for Symbolic Regression

Symbolic regression is a task aimed at identifying patterns in data and representing them through mathematical expressions, generally involving skeleton prediction and constant optimization. Many methods have achieved some success, however they treat variables and symbols merely as characters of natural language without considering their mathematical essence. This paper introduces the operator feature neural network (OF-Net) which employs operator representation for expressions and proposes an implicit feature encoding method for the intrinsic mathematical operational logic of operators. By substituting operator features for numeric loss, we can predict the combination of operators of target expressions. We evaluate the model on public datasets, and the results demonstrate that the model achieves superior recovery rates and high $R^2$ scores. With the discussion of the results, we analyze the merit and demerit of OF-Net and propose optimizing schemes.

GPSFormer: A Global Perception and Local Structure Fitting-based Transformer for Point Cloud Understanding

Despite the significant advancements in pre-training methods for point cloud understanding, directly capturing intricate shape information from irregular point clouds without reliance on external data remains a formidable challenge. To address this problem, we propose GPSFormer, an innovative Global Perception and Local Structure Fitting-based Transformer, which learns detailed shape information from point clouds with remarkable precision. The core of GPSFormer is the Global Perception Module (GPM) and the Local Structure Fitting Convolution (LSFConv). Specifically, GPM utilizes Adaptive Deformable Graph Convolution (ADGConv) to identify short-range dependencies among similar features in the feature space and employs Multi-Head Attention (MHA) to learn long-range dependencies across all positions within the feature space, ultimately enabling flexible learning of contextual representations. Inspired by Taylor series, we design LSFConv, which learns both low-order fundamental and high-order refinement information from explicitly encoded local geometric structures. Integrating the GPM and LSFConv as fundamental components, we construct GPSFormer, a cutting-edge Transformer that effectively captures global and local structures of point clouds. Extensive experiments validate GPSFormer's effectiveness in three point cloud tasks: shape classification, part segmentation, and few-shot learning. The code of GPSFormer is available at \url{https://github.com/changshuowang/GPSFormer}.

DN-CL: Deep Symbolic Regression against Noise via Contrastive Learning

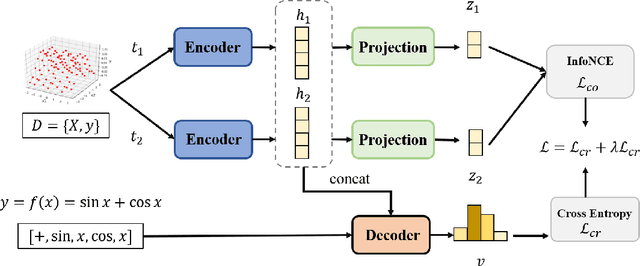
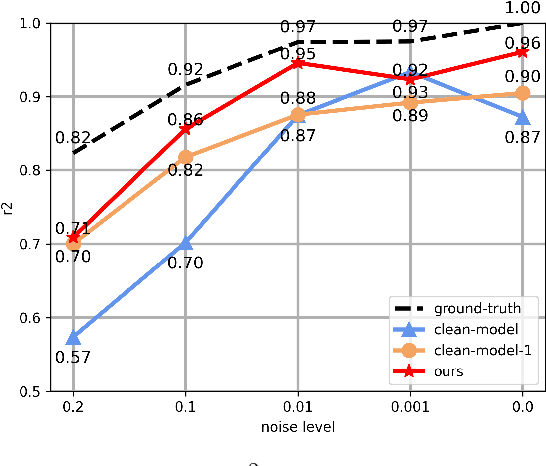
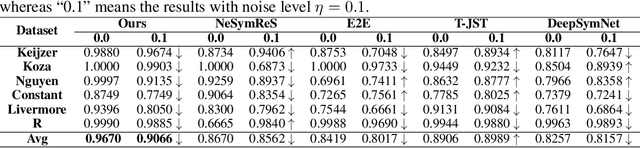
Noise ubiquitously exists in signals due to numerous factors including physical, electronic, and environmental effects. Traditional methods of symbolic regression, such as genetic programming or deep learning models, aim to find the most fitting expressions for these signals. However, these methods often overlook the noise present in real-world data, leading to reduced fitting accuracy. To tackle this issue, we propose \textit{\textbf{D}eep Symbolic Regression against \textbf{N}oise via \textbf{C}ontrastive \textbf{L}earning (DN-CL)}. DN-CL employs two parameter-sharing encoders to embed data points from various data transformations into feature shields against noise. This model treats noisy data and clean data as different views of the ground-truth mathematical expressions. Distances between these features are minimized, utilizing contrastive learning to distinguish between 'positive' noise-corrected pairs and 'negative' contrasting pairs. Our experiments indicate that DN-CL demonstrates superior performance in handling both noisy and clean data, presenting a promising method of symbolic regression.

MLLM-SR: Conversational Symbolic Regression base Multi-Modal Large Language Models

Formulas are the language of communication between humans and nature. It is an important research topic of artificial intelligence to find expressions from observed data to reflect the relationship between each variable in the data, which is called a symbolic regression problem. The existing symbolic regression methods directly generate expressions according to the given observation data, and we cannot require the algorithm to generate expressions that meet specific requirements according to the known prior knowledge. For example, the expression needs to contain $\sin$ or be symmetric, and so on. Even if it can, it often requires very complex operations, which is very inconvenient. In this paper, based on multi-modal large language models, we propose MLLM-SR, a conversational symbolic regression method that can generate expressions that meet the requirements simply by describing the requirements with natural language instructions. By experimenting on the Nguyen dataset, we can demonstrate that MLLM-SR leads the state-of-the-art baselines in fitting performance. More notably, we experimentally demonstrate that MLLM-SR can well understand the prior knowledge we add to the natural language instructions. Moreover, the addition of prior knowledge can effectively guide MLLM-SR to generate correct expressions.

Seeing the Forest through the Trees: Data Leakage from Partial Transformer Gradients

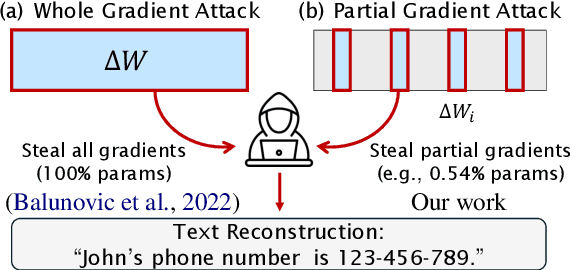
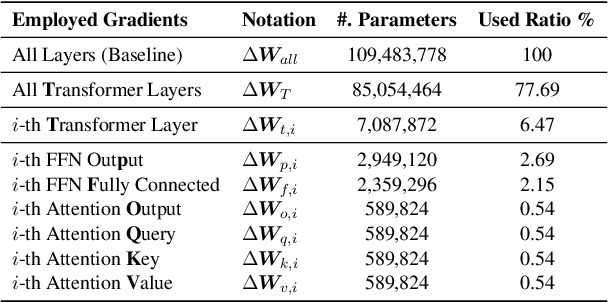
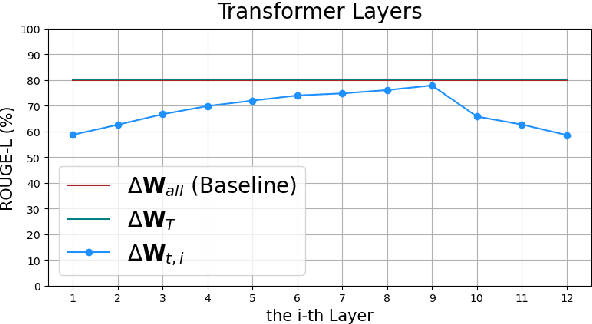
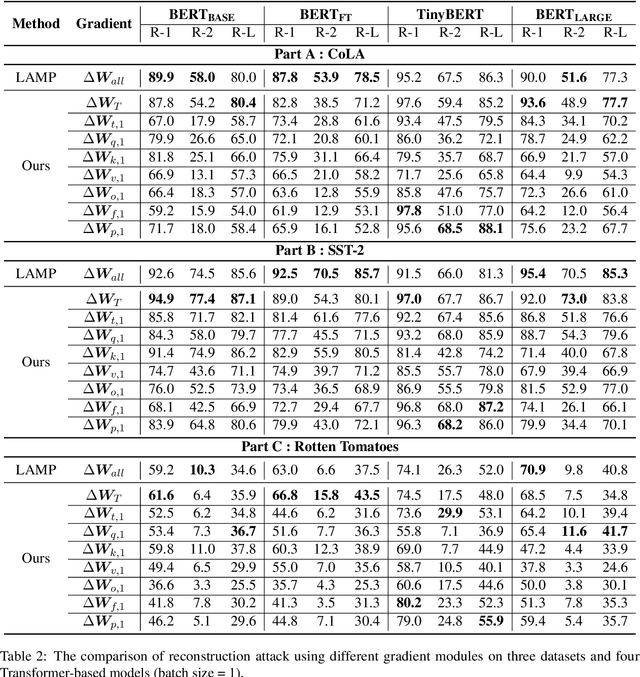
Recent studies have shown that distributed machine learning is vulnerable to gradient inversion attacks, where private training data can be reconstructed by analyzing the gradients of the models shared in training. Previous attacks established that such reconstructions are possible using gradients from all parameters in the entire models. However, we hypothesize that most of the involved modules, or even their sub-modules, are at risk of training data leakage, and we validate such vulnerabilities in various intermediate layers of language models. Our extensive experiments reveal that gradients from a single Transformer layer, or even a single linear component with 0.54% parameters, are susceptible to training data leakage. Additionally, we show that applying differential privacy on gradients during training offers limited protection against the novel vulnerability of data disclosure.

Closed-form Symbolic Solutions: A New Perspective on Solving Partial Differential Equations

Solving partial differential equations (PDEs) in Euclidean space with closed-form symbolic solutions has long been a dream for mathematicians. Inspired by deep learning, Physics-Informed Neural Networks (PINNs) have shown great promise in numerically solving PDEs. However, since PINNs essentially approximate solutions within the continuous function space, their numerical solutions fall short in both precision and interpretability compared to symbolic solutions. This paper proposes a novel framework: a closed-form \textbf{Sym}bolic framework for \textbf{PDE}s (SymPDE), exploring the use of deep reinforcement learning to directly obtain symbolic solutions for PDEs. SymPDE alleviates the challenges PINNs face in fitting high-frequency and steeply changing functions. To our knowledge, no prior work has implemented this approach. Experiments on solving the Poisson's equation and heat equation in time-independent and spatiotemporal dynamical systems respectively demonstrate that SymPDE can provide accurate closed-form symbolic solutions for various types of PDEs.

Generative Pre-Trained Transformer for Symbolic Regression Base In-Context Reinforcement Learning

The mathematical formula is the human language to describe nature and is the essence of scientific research. Finding mathematical formulas from observational data is a major demand of scientific research and a major challenge of artificial intelligence. This area is called symbolic regression. Originally symbolic regression was often formulated as a combinatorial optimization problem and solved using GP or reinforcement learning algorithms. These two kinds of algorithms have strong noise robustness ability and good Versatility. However, inference time usually takes a long time, so the search efficiency is relatively low. Later, based on large-scale pre-training data proposed, such methods use a large number of synthetic data points and expression pairs to train a Generative Pre-Trained Transformer(GPT). Then this GPT can only need to perform one forward propagation to obtain the results, the advantage is that the inference speed is very fast. However, its performance is very dependent on the training data and performs poorly on data outside the training set, which leads to poor noise robustness and Versatility of such methods. So, can we combine the advantages of the above two categories of SR algorithms? In this paper, we propose \textbf{FormulaGPT}, which trains a GPT using massive sparse reward learning histories of reinforcement learning-based SR algorithms as training data. After training, the SR algorithm based on reinforcement learning is distilled into a Transformer. When new test data comes, FormulaGPT can directly generate a "reinforcement learning process" and automatically update the learning policy in context. Tested on more than ten datasets including SRBench, formulaGPT achieves the state-of-the-art performance in fitting ability compared with four baselines. In addition, it achieves satisfactory results in noise robustness, versatility, and inference efficiency.

MMSR: Symbolic Regression is a Multimodal Task

Mathematical formulas are the crystallization of human wisdom in exploring the laws of nature for thousands of years. Describing the complex laws of nature with a concise mathematical formula is a constant pursuit of scientists and a great challenge for artificial intelligence. This field is called symbolic regression. Symbolic regression was originally formulated as a combinatorial optimization problem, and GP and reinforcement learning algorithms were used to solve it. However, GP is sensitive to hyperparameters, and these two types of algorithms are inefficient. To solve this problem, researchers treat the mapping from data to expressions as a translation problem. And the corresponding large-scale pre-trained model is introduced. However, the data and expression skeletons do not have very clear word correspondences as the two languages do. Instead, they are more like two modalities (e.g., image and text). Therefore, in this paper, we proposed MMSR. The SR problem is solved as a pure multimodal problem, and contrastive learning is also introduced in the training process for modal alignment to facilitate later modal feature fusion. It is worth noting that in order to better promote the modal feature fusion, we adopt the strategy of training contrastive learning loss and other losses at the same time, which only needs one-step training, instead of training contrastive learning loss first and then training other losses. Because our experiments prove training together can make the feature extraction module and feature fusion module running-in better. Experimental results show that compared with multiple large-scale pre-training baselines, MMSR achieves the most advanced results on multiple mainstream datasets including SRBench.