DN-CL: Deep Symbolic Regression against Noise via Contrastive Learning

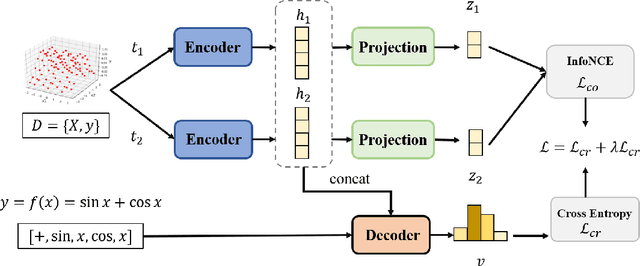
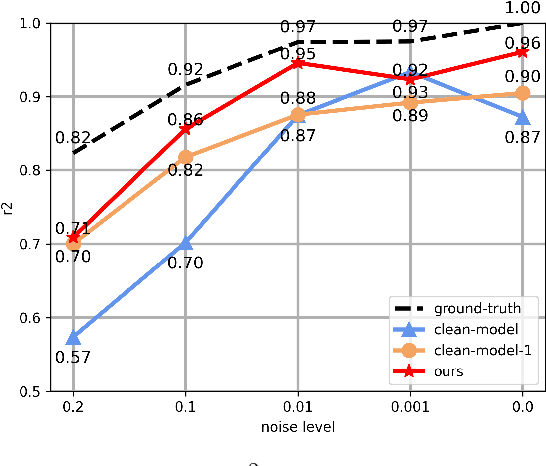
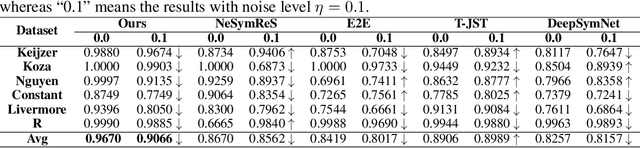
Noise ubiquitously exists in signals due to numerous factors including physical, electronic, and environmental effects. Traditional methods of symbolic regression, such as genetic programming or deep learning models, aim to find the most fitting expressions for these signals. However, these methods often overlook the noise present in real-world data, leading to reduced fitting accuracy. To tackle this issue, we propose \textit{\textbf{D}eep Symbolic Regression against \textbf{N}oise via \textbf{C}ontrastive \textbf{L}earning (DN-CL)}. DN-CL employs two parameter-sharing encoders to embed data points from various data transformations into feature shields against noise. This model treats noisy data and clean data as different views of the ground-truth mathematical expressions. Distances between these features are minimized, utilizing contrastive learning to distinguish between 'positive' noise-corrected pairs and 'negative' contrasting pairs. Our experiments indicate that DN-CL demonstrates superior performance in handling both noisy and clean data, presenting a promising method of symbolic regression.