Operator Feature Neural Network for Symbolic Regression

Symbolic regression is a task aimed at identifying patterns in data and representing them through mathematical expressions, generally involving skeleton prediction and constant optimization. Many methods have achieved some success, however they treat variables and symbols merely as characters of natural language without considering their mathematical essence. This paper introduces the operator feature neural network (OF-Net) which employs operator representation for expressions and proposes an implicit feature encoding method for the intrinsic mathematical operational logic of operators. By substituting operator features for numeric loss, we can predict the combination of operators of target expressions. We evaluate the model on public datasets, and the results demonstrate that the model achieves superior recovery rates and high $R^2$ scores. With the discussion of the results, we analyze the merit and demerit of OF-Net and propose optimizing schemes.

DN-CL: Deep Symbolic Regression against Noise via Contrastive Learning

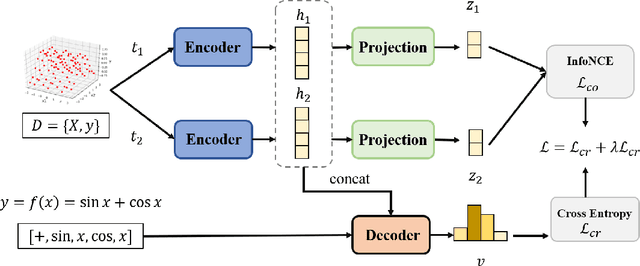
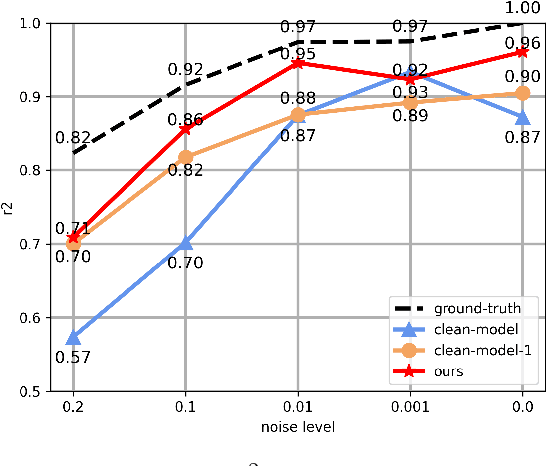
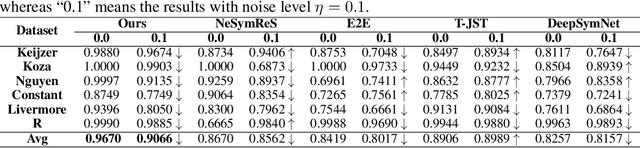
Noise ubiquitously exists in signals due to numerous factors including physical, electronic, and environmental effects. Traditional methods of symbolic regression, such as genetic programming or deep learning models, aim to find the most fitting expressions for these signals. However, these methods often overlook the noise present in real-world data, leading to reduced fitting accuracy. To tackle this issue, we propose \textit{\textbf{D}eep Symbolic Regression against \textbf{N}oise via \textbf{C}ontrastive \textbf{L}earning (DN-CL)}. DN-CL employs two parameter-sharing encoders to embed data points from various data transformations into feature shields against noise. This model treats noisy data and clean data as different views of the ground-truth mathematical expressions. Distances between these features are minimized, utilizing contrastive learning to distinguish between 'positive' noise-corrected pairs and 'negative' contrasting pairs. Our experiments indicate that DN-CL demonstrates superior performance in handling both noisy and clean data, presenting a promising method of symbolic regression.

MLLM-SR: Conversational Symbolic Regression base Multi-Modal Large Language Models

Formulas are the language of communication between humans and nature. It is an important research topic of artificial intelligence to find expressions from observed data to reflect the relationship between each variable in the data, which is called a symbolic regression problem. The existing symbolic regression methods directly generate expressions according to the given observation data, and we cannot require the algorithm to generate expressions that meet specific requirements according to the known prior knowledge. For example, the expression needs to contain $\sin$ or be symmetric, and so on. Even if it can, it often requires very complex operations, which is very inconvenient. In this paper, based on multi-modal large language models, we propose MLLM-SR, a conversational symbolic regression method that can generate expressions that meet the requirements simply by describing the requirements with natural language instructions. By experimenting on the Nguyen dataset, we can demonstrate that MLLM-SR leads the state-of-the-art baselines in fitting performance. More notably, we experimentally demonstrate that MLLM-SR can well understand the prior knowledge we add to the natural language instructions. Moreover, the addition of prior knowledge can effectively guide MLLM-SR to generate correct expressions.

Closed-form Symbolic Solutions: A New Perspective on Solving Partial Differential Equations

Solving partial differential equations (PDEs) in Euclidean space with closed-form symbolic solutions has long been a dream for mathematicians. Inspired by deep learning, Physics-Informed Neural Networks (PINNs) have shown great promise in numerically solving PDEs. However, since PINNs essentially approximate solutions within the continuous function space, their numerical solutions fall short in both precision and interpretability compared to symbolic solutions. This paper proposes a novel framework: a closed-form \textbf{Sym}bolic framework for \textbf{PDE}s (SymPDE), exploring the use of deep reinforcement learning to directly obtain symbolic solutions for PDEs. SymPDE alleviates the challenges PINNs face in fitting high-frequency and steeply changing functions. To our knowledge, no prior work has implemented this approach. Experiments on solving the Poisson's equation and heat equation in time-independent and spatiotemporal dynamical systems respectively demonstrate that SymPDE can provide accurate closed-form symbolic solutions for various types of PDEs.

Generative Pre-Trained Transformer for Symbolic Regression Base In-Context Reinforcement Learning

The mathematical formula is the human language to describe nature and is the essence of scientific research. Finding mathematical formulas from observational data is a major demand of scientific research and a major challenge of artificial intelligence. This area is called symbolic regression. Originally symbolic regression was often formulated as a combinatorial optimization problem and solved using GP or reinforcement learning algorithms. These two kinds of algorithms have strong noise robustness ability and good Versatility. However, inference time usually takes a long time, so the search efficiency is relatively low. Later, based on large-scale pre-training data proposed, such methods use a large number of synthetic data points and expression pairs to train a Generative Pre-Trained Transformer(GPT). Then this GPT can only need to perform one forward propagation to obtain the results, the advantage is that the inference speed is very fast. However, its performance is very dependent on the training data and performs poorly on data outside the training set, which leads to poor noise robustness and Versatility of such methods. So, can we combine the advantages of the above two categories of SR algorithms? In this paper, we propose \textbf{FormulaGPT}, which trains a GPT using massive sparse reward learning histories of reinforcement learning-based SR algorithms as training data. After training, the SR algorithm based on reinforcement learning is distilled into a Transformer. When new test data comes, FormulaGPT can directly generate a "reinforcement learning process" and automatically update the learning policy in context. Tested on more than ten datasets including SRBench, formulaGPT achieves the state-of-the-art performance in fitting ability compared with four baselines. In addition, it achieves satisfactory results in noise robustness, versatility, and inference efficiency.

MMSR: Symbolic Regression is a Multimodal Task

Mathematical formulas are the crystallization of human wisdom in exploring the laws of nature for thousands of years. Describing the complex laws of nature with a concise mathematical formula is a constant pursuit of scientists and a great challenge for artificial intelligence. This field is called symbolic regression. Symbolic regression was originally formulated as a combinatorial optimization problem, and GP and reinforcement learning algorithms were used to solve it. However, GP is sensitive to hyperparameters, and these two types of algorithms are inefficient. To solve this problem, researchers treat the mapping from data to expressions as a translation problem. And the corresponding large-scale pre-trained model is introduced. However, the data and expression skeletons do not have very clear word correspondences as the two languages do. Instead, they are more like two modalities (e.g., image and text). Therefore, in this paper, we proposed MMSR. The SR problem is solved as a pure multimodal problem, and contrastive learning is also introduced in the training process for modal alignment to facilitate later modal feature fusion. It is worth noting that in order to better promote the modal feature fusion, we adopt the strategy of training contrastive learning loss and other losses at the same time, which only needs one-step training, instead of training contrastive learning loss first and then training other losses. Because our experiments prove training together can make the feature extraction module and feature fusion module running-in better. Experimental results show that compared with multiple large-scale pre-training baselines, MMSR achieves the most advanced results on multiple mainstream datasets including SRBench.

Discovering Mathematical Formulas from Data via GPT-guided Monte Carlo Tree Search

Finding a concise and interpretable mathematical formula that accurately describes the relationship between each variable and the predicted value in the data is a crucial task in scientific research, as well as a significant challenge in artificial intelligence. This problem is referred to as symbolic regression, which is an NP-hard problem. In the previous year, a novel symbolic regression methodology utilizing Monte Carlo Tree Search (MCTS) was advanced, achieving state-of-the-art results on a diverse range of datasets. although this algorithm has shown considerable improvement in recovering target expressions compared to previous methods, the lack of guidance during the MCTS process severely hampers its search efficiency. Recently, some algorithms have added a pre-trained policy network to guide the search of MCTS, but the pre-trained policy network generalizes poorly. To optimize the trade-off between efficiency and versatility, we introduce SR-GPT, a novel algorithm for symbolic regression that integrates Monte Carlo Tree Search (MCTS) with a Generative Pre-Trained Transformer (GPT). By using GPT to guide the MCTS, the search efficiency of MCTS is significantly improved. Next, we utilize the MCTS results to further refine the GPT, enhancing its capabilities and providing more accurate guidance for the MCTS. MCTS and GPT are coupled together and optimize each other until the target expression is successfully determined. We conducted extensive evaluations of SR-GPT using 222 expressions sourced from over 10 different symbolic regression datasets. The experimental results demonstrate that SR-GPT outperforms existing state-of-the-art algorithms in accurately recovering symbolic expressions both with and without added noise.

MetaSymNet: A Dynamic Symbolic Regression Network Capable of Evolving into Arbitrary Formulations

Mathematical formulas serve as the means of communication between humans and nature, encapsulating the operational laws governing natural phenomena. The concise formulation of these laws is a crucial objective in scientific research and an important challenge for artificial intelligence (AI). While traditional artificial neural networks (MLP) excel at data fitting, they often yield uninterpretable black box results that hinder our understanding of the relationship between variables x and predicted values y. Moreover, the fixed network architecture in MLP often gives rise to redundancy in both network structure and parameters. To address these issues, we propose MetaSymNet, a novel neural network that dynamically adjusts its structure in real-time, allowing for both expansion and contraction. This adaptive network employs the PANGU meta function as its activation function, which is a unique type capable of evolving into various basic functions during training to compose mathematical formulas tailored to specific needs. We then evolve the neural network into a concise, interpretable mathematical expression. To evaluate MetaSymNet's performance, we compare it with four state-of-the-art symbolic regression algorithms across more than 10 public datasets comprising 222 formulas. Our experimental results demonstrate that our algorithm outperforms others consistently regardless of noise presence or absence. Furthermore, we assess MetaSymNet against MLP and SVM regarding their fitting ability and extrapolation capability, these are two essential aspects of machine learning algorithms. The findings reveal that our algorithm excels in both areas. Finally, we compared MetaSymNet with MLP using iterative pruning in network structure complexity. The results show that MetaSymNet's network structure complexity is obviously less than MLP under the same goodness of fit.